Привести уравнения к параметрическому виду и найти площади фигур ограниченных петлей кривой

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Криволинейная трапеция и ее площадь. 11 класс.Скачать

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a , x = b , а также непрерывной (неотрицательной или неположительной) функцией y = f ( x ) . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x = a , x = b , ось O x и параметрически заданная кривая x = φ ( t ) y = ψ ( t ) , а функции x = φ ( t ) и y = ψ ( t ) являются непрерывными на интервале α ; β , α β , x = φ ( t ) будет непрерывно возрастать на нем и φ ( α ) = a , φ ( β ) = b .

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S ( G ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t .

Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :

S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t

Учитывая монотонное убывание функции x = φ ( t ) на интервале β ; α , β α , нужная формула принимает вид S ( G ) = — ∫ β α ψ ( t ) · φ ‘ ( t ) d t .

Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x = 2 cos t y = 3 sin t .

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3 . См на иллюстрацию:

Попробуем найти площадь 1 4 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x ∈ a ; b = 0 ; 2 . Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x = φ ( t ) = 2 cos t y = ψ ( t ) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z

При k , равном 0 , мы получим интервал β ; α = 0 ; π 2 . Функция x = φ ( t ) = 2 cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

— ∫ 0 π 2 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 ( 1 — cos ( 2 t ) d t = = 3 · t — sin ( 2 t ) 2 0 π 2 = 3 · π 2 — sin 2 · π 2 2 — 0 — sin 2 · 0 2 = 3 π 2

Значит, площадь фигуры, заданной исходной кривой, будет равна S ( G ) = 4 · 3 π 2 = 6 π .

Ответ: S ( G ) = 6 π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x ∈ a ; b = — 2 ; 2 . В этом случае у нас бы получилось:

φ ( α ) = a ⇔ 2 cos α = — 2 ⇔ α = π + π k , k ∈ Z , φ ( β ) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k , k ∈ Z

Таким образом, при k равном 0 , мы получили β ; α = 0 ; π . Функция x = φ ( t ) = 2 cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

— ∫ 0 π 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π ( 1 — cos ( 2 t ) d t = = 3 · t — sin ( 2 t ) 2 0 π = 3 · π — sin 2 · π 2 — 0 — sin 2 · 0 2 = 3 π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x = a · cos t y = b · sin t . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса S э л и п с а = πab .

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x = R · cos t y = R · sin t , где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R : S к р у г а = πR 2 .

Разберем еще одну задачу.

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x = 3 cos 3 t y = 2 sin 3 t .

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x = a · cos 3 t y = a · sin 3 t .

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t .

Данные функции являются определенными для всех действительных значений t . Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t для некоторых t = t 0 ∈ 0 ; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8 , получим точки x 0 ; y 0 = ( φ ( t 0 ) ; ψ ( t 0 ) ) .

Составим таблицу итоговых значений:

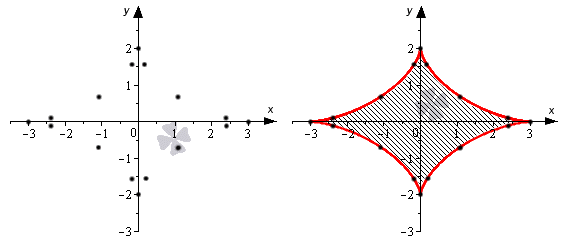
После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :

φ ( α ) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ ( β ) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z

Если k равен 0 , то у нас получится интервал β ; α = 0 ; π 2 , и функция x = φ ( t ) = 3 cos 3 t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

— ∫ 0 π 2 2 sin 3 t · 3 cos 3 t ‘ d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · ( 1 — sin 2 t ) d t = 18 ∫ 0 π 2 sin 4 t d t — ∫ 0 π 2 sin 6 t d t

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу J n ( x ) = — cos x · sin n — 1 ( x ) n + n — 1 n J n — 2 ( x ) , где J n ( x ) = ∫ sin n x d x .

∫ sin 4 t d t = — cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = — cos t · sin 3 t 4 + 3 4 — cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = — cos t · sin 3 t 4 — 3 cos t · sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = — cos t · sin 3 t 4 — 3 cos t · sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = — cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = — cos t · sin 5 t 6 0 π 2 + 5 6 ∫ 0 π 2 sin 4 t d t = 5 6 · 3 π 16 = 15 π 96

Мы вычислили площадь четверти фигуры. Она равна 18 ∫ 0 π 2 sin 4 t d t — ∫ 0 π 2 sin 6 t d t = 18 3 π 16 — 15 π 96 = 9 π 16 .

Если мы умножим это значение на 4 , получим площадь всей фигуры – 9 π 4 .

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x = a · cos 3 t y = a · sin 3 t , можно найти по формуле S а с т р о и д ы = 3 πa 2 8 , а площадь фигуры, которая ограничена линией x = a · cos 3 t y = b · sin 3 t , считается по формуле S = 3 πab 8 .

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Вычисление площадей фигур в различных системах координат

Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:

Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .

Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше

Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).

Решение. Имеем: (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:

Воспользовавшись формулой из таблицы при , получим:

Значит, окончательно имеем:

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая задана в параметрической форме

где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

Пример 5. Вычислить площадь эллипса, заданного параметрически

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому

Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .

Разобьем данный сектор на частей лучами

и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.

Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

В то же время по определению определенного интеграла

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).

💥 Видео

Площадь фигуры, ограниченной линией, заданной параметрически. Площадь, ограниченная эллипсомСкачать

Геометрический смысл определенного интеграла (2)Скачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Определённый интеграл. ПлощадьСкачать

Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать

Площади 12Скачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Как построить кривую, заданную параметрическиСкачать

Найти площадь фигуры, ограниченной линиямиСкачать

Нахождение площадей фигур, ограниченных графикамиСкачать

Площадь фигуры, заданной в полярной системе координатСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать