Привести уравнение кривых второго порядка к каноническому виду с помощью параллельного переноса

Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать

Приведение кривой второго порядка к каноническому виду

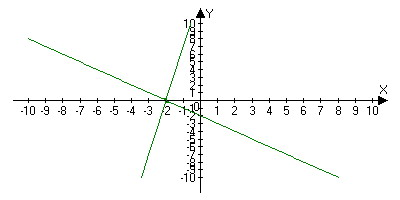
Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

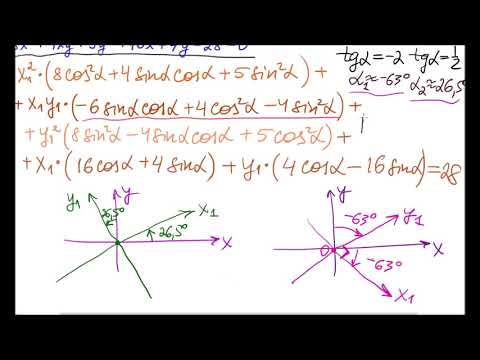
Привести уравнение кривых второго порядка к каноническому виду с помощью параллельного переноса

УЖЕ увидели
после двух заходов в ленту избранного не удержался

popk0rN
пожалуйста, читайте правила! Это реально неприятно, когда несколько тысяч людей видят такое полотнище на половину френдленты

большое спасибо, 2 задание я решил, но вот с 3 снова проблема, когда я дополняю до полного квадрата у меня получается 0

Мне очень сложно здесь набирать такие вещи.
разложить по формуле разность квадратов
произведение двух множителей равно 0, когда один из них равен 0
Будут два линейных уравнения
Одно , например,
у с чертой=2х с чертой + корень из 10

Вы в конце перестали ставить черточки. А ведь это будут уравнения прямых в повернутой системе координат (вы поворачиваете систему на угол тангенс которого равен 1/3 и в этой системе уравнения прямых будут выглядеть так ужасно)
Но в исходной системе ХОУ они будут выглядеть проще
Можно схитрить и строить их в исходной. Положить х=0 (х без черты) и подставить в исходное уравнение, получится у=-2 и у=14 (вот вам по точке с каждой прямой), аналогично если у=0

Видео:Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Видео:Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Использование линейных операторов для Приведения кривой второго порядка к каноническому виду

ИСПОЛЬЗОВАНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ ДЛЯ Приведения кривой второго порядка к каноническому виду

ФГБОУ «Шадринский государственный педагогический институт»,

Руководитель: ст. преподаватель

Вопрос о кривых второго порядка встаёт, когда мы на плоскости рассматриваем некоторое геометрическое место точек, задаваемое уравнением вида: (*)

Из такого выражения довольно проблематично сразу определить вид кривой, её свойства, не говоря уже о вычислении эксцентриситета, фокуса и других не менее важных параметров. Легко определить вид линии и ее свойства по каноническому уравнению. Привести данное уравнение к каноническому виду можно разными способами.

Геометрически приведение кривой к каноническому виду состоит из двух этапов:

1. Поворот системы координат, цель которого освободиться от слагаемого xy.

2. Параллельный перенос системы координат, цель которого освободиться от слагаемых с x и с y.

Покажем как для этой цели могут быть использованы линейные операторы.

Чтобы освободиться от слагаемого с xy рассмотрим часть уравнения, где все слагаемые имеют вторую степень . Выражения такого вида можно считать квадратичной формой. Приведем квадратичную форму к каноническому виду с помощью ортогональных преобразований, тем самым освободимся от слагаемого .

Затем выделяем полные квадраты так, чтобы у нас исчезли соответствующие слагаемые первой степени.

Теперь рассмотрим, как эти шаги выполнять на практике.

Во-первых, составляем матрицу квадратичной формы:

.

Далее находим собственные числа матрицы , для этого решаем уравнение ( – единичная матрица).

— корни этого уравнения, собственные числа матрицы .

Зная собственные числа, находим собственные векторы из следующих уравнений:

где — i—е собственное число, а и — соответствующие координаты собственного вектора, который соответствует i-му собственному числу. Собственный вектор определён с точностью до его длины. Т. е. все векторы, сонаправленные какому-либо собственному вектору, также являются собственными векторами.

Для наших целей необходимы ортонормированные собственные вектора, т. е. такие, которые удовлетворяют условию: (модуль вектора равен единице). Матрица перехода выглядит следующим образом:

Это – матрица поворота. Она производит следующее действие:

то есть приводит выражение к виду

(квадратичную форму к каноническому виду).

С помощью следующего действия находим новые коэффициенты при переменных первой степени

После всех преобразований уравнение (*) примет вид:

Далее переходим ко второму этапу – собираем полные квадраты каждой из переменных:

где

Далее делаем замену:

.

И после подстановки получаем уравнение вида:

.

Существует всего девять типов кривых второго порядка.

Собствен — ные значения

Уравнение после первого шага

Тип линий и ее каноническое уравнение

эллипс ;

мнимый эллипс ;

гипербола ;

пара действительных пересекающихся прямых

;

пара мнимых пересекающихся прямых

,

,

парабола , ()

пара действительных параллельных

прямых, ();

пара мнимых параллельных прямых, ( )

пара совпадающих прямых , ()

Пример. Линия второго порядка задана общим уравнением . Определить, какая это линия и изобразить ее.

Рассмотрим члены второго порядка из уравнения (квадратичную форму) , матрица этой квадратичной формы .

Приведем квадратичную форму к каноническому виду ортогональным преобразованием: . . . Находим нормированные собственные векторы для и .

. .

Собственный вектор: .

Нормируем:

. .

Собственный вектор .

Нормируем:

Уравнение линии будет таким: .

Выделим полные квадраты:

.

Тогда

Уравнение линии примет вид: или — каноническое уравнение эллипса.

Изобразим первоначальную систему , систему после поворота и после параллельного переноса . В последней системе строим эллипс с полуосями 4 и 3 единицы.

1. Беклемишев, аналитической геометрии и линейной алгебры [Текст]./ . — М.: Наука, 1980.

2. Кузнецов, заданий по высшей математике [Текст]./ . — М.: Высшая школа, 1983.

📽️ Видео

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

2. Приведение уравнений второго порядка к каноническому видуСкачать

Видеоурок "Приведение к каноническому виду"Скачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертежСкачать

Приведение общего уравнения линии второго порядка к каноническому видуСкачать

Приведение кривой второго порядка к каноническому виду. ТемаСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Семинар Аналитическая геометрия. Кривые и поверхности второго порядка.Скачать

Лекция 7. Приведение общего уравнения кривой второго порядка к каноническому видуСкачать