Привести систему уравнений к ступенчатому виду онлайн (3 видео)

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Содержание

Предупреждение
Метод Гаусса
Примеры решения системы линейных уравнений методом Гаусса
Приведенные ступенчатые матрицы
Приведенные ступенчатые матрицы
Ступенчатая матрица
Приведенная ступенчатая матрица
Преобразование матрицы к приведенному ступенчатому виду по строкам (каноническому виду по строкам)
Решение систем линейных уравнений
🌟 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Приведение матрицы к ступенчатому видуСкачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

перемена местами двух уравнений в системе,
умножение какого-либо уравнения в системе на ненулевое действительное число,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

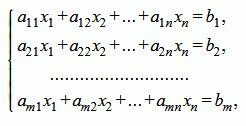Привести систему уравнений к ступенчатому виду онлайн

(1)

Запишем систему (1) в матричном виде:

Ax=b

(2)

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

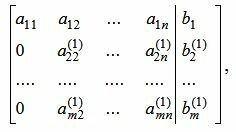(5)

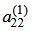
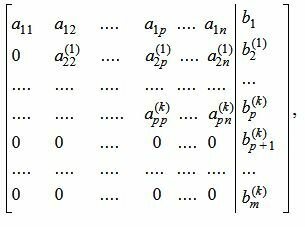На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 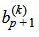. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

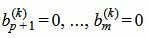
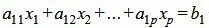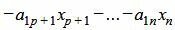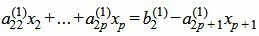Пусть . Тогда

(7)

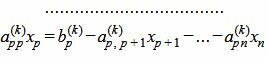Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

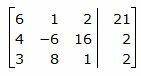Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

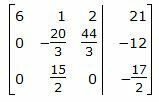Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

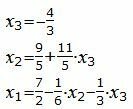Подставив верхние выражения в нижние, получим решение.

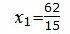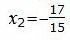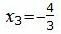Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

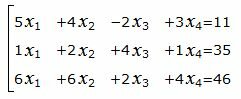Матричный вид записи: Ax=b, где

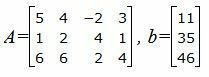Для решения системы, построим расширенную матрицу:

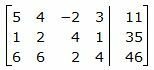Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

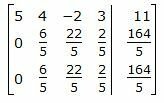Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

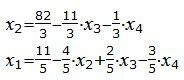где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

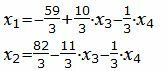где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

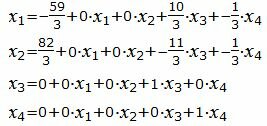Тогда векторное решение можно представить так:

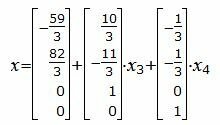где x₃, x₄− произвольные действительные числа.

Видео:Приведение матрицы к ступенчатому виду. Алгоритм ГауссаСкачать

Приведенные ступенчатые матрицы

Этот онлайн калькулятор преобразует заданную матрицу к приведенному ступенчатому виду по строкам (каноническому виду по строкам) и показывает решение по шагам.

Этот онлайн калькулятор проводит пошаговое преобразование заданной матрицы к приведенному ступенчатому виду. Помимо решения — приведенной ступенчатой матрицы — калькулятор также показывает использованные на каждом шаге элементарные преобразования строк. Определения терминов, для тех, кто забыл, приведены, как обычно, под калькулятором.

Приведенные ступенчатые матрицы

Ступенчатая матрица

Ступенчатой матрицей, или матрицей ступенчатого вида по строкам, называется матрица, такая что

все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками
ведущий элемент (первый, считая слева направо, ненулевой элемент строки) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

Примеры ступенчатых матриц:

нулевая матрица
однострочная матрица
единичная матрица
верхнетреугольная матрица

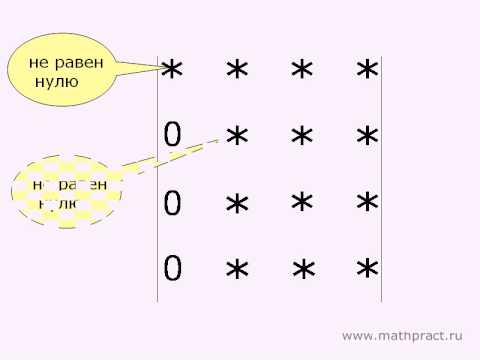
Матрица, приведенная ниже, также является ступенчатой матрицей:

Приведенная ступенчатая матрица

Ступенчатая матрица называется приведенной, если матрица, составленная из всех ее основных столбцов, является единичной матрицей (столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы).

То есть, приведенная ступенчатая матрица не имеет нулевых строк, и все ведущие элементы ее строк равны единице. При этом все элементы основных столбцов, помимо ведущих элементов, являются нулями.

Матрица, приведенная ниже, является приведенной ступенчатой матрицей:

Преобразование матрицы к приведенному ступенчатому виду по строкам (каноническому виду по строкам)

Для приведения матрицы к ступенчатому или приведенному ступенчатому виду используются элементарные преобразования строк. Каждая матрица может быть преобразована к уникальному приведенному ступенчатому виду.

Элементарные преобразования строк:

перестановка местами любых двух строк матрицы

умножение любой строки матрицы на ненулевую константу

прибавление к любой строке матрицы другой строки, умноженной на некоторую ненулевую константу

Эти преобразования и используются калькулятором выше для приведения матрицы к каноническому виду по строкам.

Видео:Метод Гаусса. Элементарные преобразования. Ранг матрицы. Ступенчатая матрица. Эквивалентная матрицаСкачать

Решение систем линейных уравнений

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).