Привести общее уравнение прямой 2x 3y 6 0 к уравнению в отрезках (5 видео)

Уравнение прямой в отрезках

В данной статье мы рассмотрим уравнение прямой в отрезках. Представим методы преобразования уравнения прямой в отрезках в уравнение прямой в общем виде и обратно. Рассмотрим численные примеры.

Уравнение прямой в отрезках представляется следующей формулой:

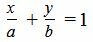Привести общее уравнение прямой 2x 3y 6 0 к уравнению в отрезках

(1)

где a и b числа, отличные от нуля.

Отметим, что числа a и b в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает прямая на осях Ox и Oy (Рис.1).

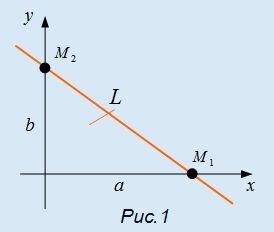Действительно. Подставляя в (1) y=0, получим x=a, если же подставить в (1) x=0, то получим y=b. Таким образом прямая L проходит через точки M₁(a, 0) и M₂(0, b).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox и Oy в точках −1 и 3, соответственно.

Решение. Подставляя значения a=−1 и b=3 в (1), получим:

Содержание

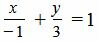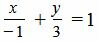Приведение уравнения прямой в отрезках к общему виду
Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках
Уравнение прямой в отрезках: описание, примеры, решение задач
Уравнение прямой в отрезках – описание и примеры
Приведение общего уравнения прямой к уравнению прямой в отрезках
Задача 62285 записать уравнение с угловым и.
Условие
Решение
📺 Видео

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Приведение уравнения прямой в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

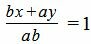Далее, умножив обе части уравнения на ab, получим:

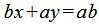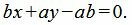Пример 2. Уравнение прямой в отрезках представлено следующим уравнением:

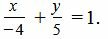Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

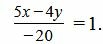Умножив обе части уравнения на −20, получим:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках

где A, B, C − отличные от нуля числа.

Сделаем следующие преобразования. Переведем свободный член C на правую часть уравнения и разделим обе части уравнения на −C:

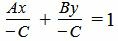(2)

Уравнение (2) можно переписать в следующем виде:

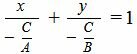(3)

Сделаем следующие обозначения:

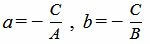Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение прямой в отрезках. Воспользуемся формулой (3). Имеем: A=5, B=8, C=−3. Подставив эти значения в формулу (3), получим:

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

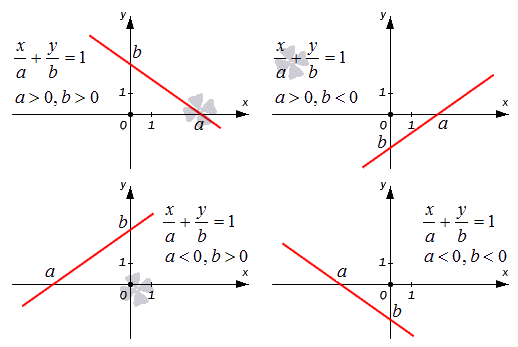
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

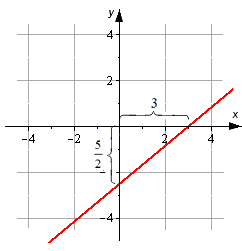
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0

Видео:Видеоурок "Общее уравнение прямой"Скачать

Задача 62285 записать уравнение с угловым и.

Условие

записать уравнение с угловым и коэффициентом в отрезках и нормальное для данных прямых и определите На каком расстоянии от начала координат они находятся 2x-3y+6=0