Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.
Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.
- Алгоритм перехода кривой второго порядка к каноническому виду
- Приведение к каноническому виду линейных уравнений с частными производными второго порядка
- Каноническое уравнение прямой на плоскости: теория, примеры, решение задач
- Понятие канонического уравнения прямой
- Канонические уравнения прямой на плоскости с a x или a y , равными нулю
- Преобразование канонического уравнения прямой в другие виды уравнений
- Как решать задачи на составление канонических уравнений
- 📸 Видео
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Алгоритм перехода кривой второго порядка к каноническому виду
Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0
Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0
Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0
Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1
Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Приведение к каноническому виду линейных уравнений с частными производными второго порядка
Федеральное агентство по образованию
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт математики, экономики и информатики
Кафедра дифференциальных и интегральных уравнений
ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА
Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………
1.1. Необходимый теоретический материал………………………..
1.2. Пример выполнения задачи1 (приведение к
каноническому виду уравнений гиперболического типа) .
1.3. Пример выполнения задачи 2 (приведение к
каноническому виду уравнений параболического типа)
1.4. Пример выполнения задачи 3 (приведение к
каноническому виду уравнений эллиптического типа) ..
1.5. Задачи для самостоятельного решения ………………….….
Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2.1. Необходимый теоретический материал …………………..
2.2. Пример выполнения задачи 4
2.3. Задачи для самостоятельного решения ……………………..
В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.
Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.
§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.
Задача. Определить тип уравнения

и привести его к каноническому виду.
1.1. Необходимый теоретический материал.
I. Тип уравнения (1) определяется знаком выражения 
· если 
· если 
· если 
Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.
Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение 



II. Чтобы привести уравнение к канонического виду, необходимо:
1. Определить коэффициенты 
2. Вычислить выражение 
3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения 
4. Записать уравнение характеристик:

5. Решить уравнение (2). Для этого:
а) разрешить уравнение (2) как квадратное уравнение относительно dy:

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):
· 
в случае уравнения гиперболического типа;
· 
в случае уравнения параболического типа;
· 
в случае уравнения эллиптического типа.
6. Ввести новые (характеристические) переменные 

· в случае уравнения гиперболического типа в качестве 

· в случае уравнения параболического типа в качестве 





· в случае уравнения эллиптического типа в качестве 

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:





8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:
· в случае уравнения гиперболического типа:

· в случае уравнения параболического типа:

· в случае уравнения эллиптического типа:

1.2. Пример выполнения задачи 1.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (9). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy: 



б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):
6. Введём характеристические переменные:
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на -100 (коэффициент при 
Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид
где
1.3. Пример выполнения задачи 2.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (12). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:


б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):
6. Введём характеристические переменные: одну из переменных 
а в качестве 


7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.
После деления на 25 (коэффициент при 
Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид
где
1.4. Пример выполнения задачи 3.
Определить тип уравнения

и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (15). Для этого:
а) разрешаем уравнение (15) как квадратное уравнение относительно dy: 
б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на 4 (коэффициент при 

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид
где
1.5. Задачи для самостоятельного решения.
Определить тип уравнения и привести его к каноническому виду.










Определить тип уравнения и привести его к каноническому виду.
Определить тип уравнения и привести его к каноническому виду.
§2. Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2. 1. Необходимый теоретический материал
В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов
· в случае уравнения гиперболического типа:

· в случае уравнения параболического типа:

· в случае уравнения эллиптического типа:

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

где 





Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).
Здесь слева расставлены соответствующие коэффициенты уравнения (11). Собирая подобные слагаемые, получим

В уравнении (16) приравняем к нулю коэффициенты при 
Откуда 


где 
2.2. Пример выполнения задачи 4
к каноническому виду и упростить группу младших производных.
9. Определим коэффициенты 
10. Вычислим выражение 

11. 
12. Запишем уравнение характеристик:

5. Решим уравнение (18). Для этого:
а) разрешаем уравнение (18) как квадратное уравнение относительно dy: 

б) найдём общие интегралы уравнений (19) (характеристики уравнения (17)):
6. Введём характеристические переменные:
13. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (17) при соответствующих производных.
14. Собирая подобные слагаемые, получим:

Теперь с помощью замены неизвестной функции (14)
упростим группу младших производных.
Пересчитаем производные, входящие в уравнение (20), используя формулы (15).
Здесь слева расставлены соответствующие коэффициенты уравнения (20). Собирая подобные слагаемые, получим

В уравнении (21) приравняем к нулю коэффициенты при 
Откуда 


Ответ. Уравнение (20) является уравнением эллиптического типа на всей плоскости XOY. Его канонический вид

где 
2.3. Задачи для самостоятельного решения
Задача 4. Привести уравнения к каноническому виду и упростить группу младших производных.










Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач
Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.
Видео:Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Понятие канонического уравнения прямой
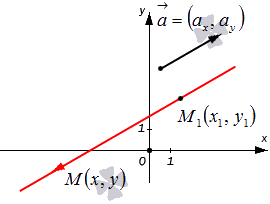
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M 1 ( x 1 , y 1 ) , а также ее направляющего вектора a → = ( a x , a y ) . Попробуем составить уравнение, которое описывало бы эту прямую.
Возьмем плавающую точку M ( x , y ) . Тогда вектор M 1 M → можно считать направляющим для исходной прямой. Его координаты будут равны x — x 1 , y — y 1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).
Множество произвольно взятых точек M ( x , y ) будут определять нужную нам прямую с направляющим вектором a → = ( a x , a y ) только в одном случае – если векторы M 1 M → и a → = ( a x , a y ) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:
Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:
M 1 M → = λ · a → , λ ∈ R
Если преобразовать полученное равенство в координатную форму, то мы получим:
x — x 1 = λ · a x y — y 1 = λ · a y
При условии, что a x ≠ 0 и a y ≠ 0 , получим:
x — x 1 = λ · a x y — y 1 = λ · a y ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y
Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x — x 1 a x = y — y 1 a y также называют уравнением прямой в каноническом виде.
Таким образом, с помощью уравнения x — x 1 a x = y — y 1 a y можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a → = ( a x , a y ) и проходит через точку M 1 ( x 1 , y 1 ) .
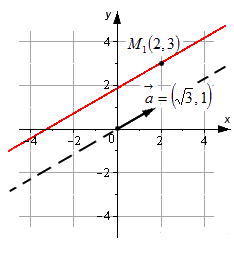
Примером уравнения подобного типа является, например, x — 2 3 = y — 3 1 . Прямая, которая задана с его помощью, проходит через M 1 ( 2 , 3 ) и имеет направляющий вектор a → = 3 , 1 . Ее можно увидеть на рисунке:
Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:
1. Если прямая, имеющая направляющий вектор a → = ( a x , a y ) , проходит через две точки – M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , то уравнение для нее может быть записано как в виде x — x 1 a x = y — y 1 a y , так и x — x 2 a x = y — y 2 a y .
2. Если заданная прямая имеет направляющий вектор с координатами a → = ( a x , a y ) , то множество всех ее векторов можно обозначить как μ · a → = ( μ · a x , μ · a y ) , μ ∈ R , μ ≠ 0 . Таким образом, любое уравнение прямой в каноническом виде x — x 1 μ · a x = y — y 1 μ · a y будет соответствовать этой прямой.
Разберем важный пример задачи на нахождение канонического уравнения.
В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M 1 ( 2 , — 4 ) и имеет направляющий вектор с координатами a → = ( 1 , — 3 ) . Запишите каноническое уравнение, описывающее данную прямую.
Решение
Для начала вспомним общий вид нужного нам канонического уравнения – x — x 1 a x = y — y 1 a y . Подставим в него имеющиеся значения x 1 = 2 , y 1 = — 4 , a x = 1 , a y = — 3 и подсчитаем:
x — x 1 a x = y — y 1 a y ⇔ x — 2 1 = y — ( — 4 ) — 3 ⇔ x — 2 1 = y + 4 — 3
Получившееся в итоге равенство и будет нужным ответом.
Ответ: x — 2 1 = y + 4 — 3
Видео:Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Канонические уравнения прямой на плоскости с a x или a y , равными нулю
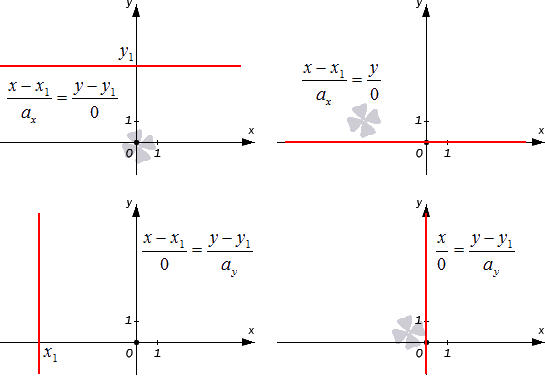
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x — x 1 a x = y — y 1 a y условной и понимать ее как равенство a y ( x — x 1 ) = a x ( y — y 1 ) .
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x — x 1 0 = y — y 1 a y при a x = 0 , а исходная прямая будет проходить через M 1 ( x 1 , y 1 ) . В таком случае она является параллельной оси ординат (если x 1 = 0 , то она будет с ней совпадать). Докажем это утверждение.
Для этой прямой вектор a → = ( 0 , a y ) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j → = ( 0 , 1 ) .
Если же нулевым является значение второго параметра, то есть a y = 0 , то мы получаем равенство вида x — x 1 a x = y — y 1 0 . Это уравнение описывает прямую, проходящую через M 1 ( x 1 , y 1 ) , которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a → = ( a x , 0 ) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i → = ( 1 , 0 ) .
Проиллюстрируем два частных случая канонического уравнения, описанные выше:
На плоскости задана прямая, параллельная оси O y . Известно, что она проходит через точку M 1 2 3 , — 1 7 . Запишите каноническое уравнение для нее.
Решение
Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j → = ( 0 , 1 ) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:
x — 2 3 0 = y — — 1 7 1 ⇔ x — 2 3 0 = y + 1 7 1
Ответ: x — 2 3 0 = y + 1 7 1
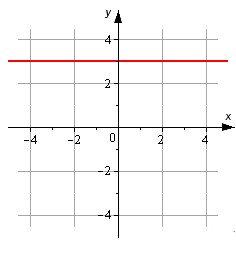
На рисунке изображена прямая. Запишите ее каноническое уравнение.
Решение
Мы видим, что исходная прямая проходит параллельно оси O x через точку M 1 ( 0 , 3 ) . Мы берем координатный вектор i → = ( 1 , 0 ) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.
x — 0 1 = y — 3 0 ⇔ x 1 = y — 3 0
Ответ: x 1 = y — 3 0
Видео:53. Приведение общего уравнения кривой к каноническому видуСкачать

Преобразование канонического уравнения прямой в другие виды уравнений
Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.
Стандартной форме записи канонического уравнения x — x 1 a x = y — y 1 a y можно поставить в соответствие систему параметрических уравнений на плоскости x = x 1 + a x · λ y = y 1 + a y · λ . Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ . После этого надо выполнить разрешение получившихся равенств относительно переменных x и y :
x — x 1 a x = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y = λ ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Покажем на примере, как именно выполняется это действие с конкретными числами.
У нас есть прямая, заданная на плоскости с помощью канонического уравнения x + 2 3 = y — 1 11 . Запишите параметрические уравнения исходной прямой.
Решение
Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x + 2 3 = λ y — 1 11 = λ .
Далее можно перейти к формулированию необходимых параметрических уравнений:
x + 2 3 = λ y — 1 11 = λ ⇔ x + 2 = 3 · λ y — 1 = 11 · λ ⇔ x = — 2 + 3 · λ y = 1 + 11 · λ
Ответ: x = — 2 + 3 · λ y = 1 + 11 · λ
Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись a b = c d можно представить в виде a · d = b · c с сохранением смысла. Значит, что x — x 1 a x = y — y 1 a y ⇔ a y ( x — x 1 ) = a x ( y — y 1 ) ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 .
Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров a y = A , — a x = B , — a y x 1 + a x y 1 = C .
Прямая на плоскости описана с помощью канонического уравнения x — 1 2 = y + 4 0 . Вычислите общее уравнение этой прямой.
Решение
Делаем указанные выше действия по порядку.
x — 1 2 = y + 4 0 ⇔ 0 · ( x — 1 ) = 2 · ( y + 4 ) ⇔ y + 4 = 0
Ответ: y + 4 = 0 .
Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.
На плоскости задана прямая с помощью уравнения x + 3 3 = y — 2 2 . Запишите уравнение этой же прямой в отрезках.
Решение
Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.
x + 3 3 = y — 2 2 ⇔ 2 · ( x + 3 ) = 3 · ( y — 2 ) ⇔ 2 x — 3 y + 6 + 2 3 = 0
Далее переходим к формулировке уравнения прямой в отрезках.
2 x — 3 y + 6 + 2 3 = 0 ⇔ 2 x — 3 y = — 6 + 2 3 ⇔ ⇔ 2 — ( 6 + 2 3 ) x — 3 — ( 6 + 2 3 ) y = 1 ⇔ x — 6 + 2 3 2 + y 6 + 2 3 3 = 1 ⇔ x — 3 + 3 + y 3 3 + 2 = 1
Ответ: x — 3 + 3 + y 3 3 + 2 = 1
Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – A x + B y + C = 0 . При условии A ≠ 0 мы можем перенести B y вправо с противоположным знаком. Получим A x + C = — B y . Теперь выносим A за скобки и преобразуем равенство так:
Получившееся уравнение мы записываем в виде пропорции: x + C A — B = y A .
У нас получилось нужное нам каноническое уравнение прямой на плоскости.
А как сделать преобразование, если B ≠ 0 ? Переносим все слагаемые, кроме A x , вправо с противоположными знаками. Получаем, что A x = — B y — C . Выносим — B за скобки:
Формируем пропорцию: x — B = y + C B A
Есть общее уравнение прямой x + 3 y — 1 = 0 . Перепишите его в каноническом виде.
Решение
Оставим с левой стороны только одну переменную x . Получим:
Теперь вынесем — 3 за скобки: x = — 3 y — 1 3 . Преобразуем равенство в пропорцию и получим необходимый ответ:
Ответ: x — 3 = y — 1 3 1
Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.
Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y
Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.
Прямая на плоскости описана с помощью системы параметрических уравнений x = 3 + 0 · λ y = — 2 — 4 · λ . Запишите каноническое уравнение для этой прямой.
Решение
Для начала преобразуем исходные уравнения в систему x = 3 + 0 · λ y = — 2 — 4 · λ . Следующим шагом будет выражение параметра в каждом уравнении:
x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4
Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x — 3 0 = y + 2 — 4
Ответ: x — 3 0 = y + 2 — 4
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Как решать задачи на составление канонических уравнений
В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.
На плоскости задана прямая, каноническое уравнение которой имеет вид x — 1 2 = y + 1 2 — 3 . Выясните, лежат ли на ней точки M 1 3 , — 3 1 2 и M 2 ( 5 , — 4 ) .
Решение
Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.
3 — 1 2 = — 3 1 2 + 1 2 — 2 ⇔ 1 = 1
Результат говорит нам, что точка M 1 3 , — 3 1 2 принадлежит исходной прямой.
Точно так же поступим и с координатами второй точки:
5 — 1 2 = — 4 + 1 2 — 3 ⇔ 2 = 7 6
Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.
Ответ: первая точка лежит на заданной прямой, а вторая нет.
Есть две точки M 1 ( 2 , 4 ) и M 2 ( — 1 , 3 ) . Будет ли прямая, которая задана в той же плоскости с помощью уравнения x — 2 0 = y — 3 2 , проходить через них?
Решение
Вспомним, что запись x — 2 0 = y — 3 2 можно понимать как 2 · ( x — 2 ) = 0 · ( y — 3 ) ⇔ x — 2 = 0 . Подставим координаты заданных точек в это равенство и проверим.
Начнем с первой точки M 1 ( 2 , 4 ) : 2 — 2 = 0 ⇔ 0 = 0
Равенство верное, значит, эта точка расположена на заданной прямой.
Подставляем данные второй точки: — 1 — 2 = 0 ⇔ — 3 = 0 .
Равенство неверное, значит, точка M 2 ( — 1 , 3 ) не лежит на исходной прямой.
Ответ: через точку M 1 ( 2 , 4 ) прямая проходит, а через M 2 ( — 1 , 3 ) нет.
Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.
Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.
Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.
Прямая на плоскости проходит через точку M 1 ( 0 , — 3 ) и через точку M 2 ( 2 , — 2 ) . Сформулируйте для этой прямой канонической уравнение.
Решение
Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M 1 M 2 → = 2 , 1 . По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:
x — 0 2 = y — ( — 3 ) 1 ⇔ x 2 = y + 3 1
Также можно использовать координаты второй точки. Тогда мы получим: x — 2 2 = y — ( — 2 ) 1 ⇔ x — 2 2 = y + 2 1
Ответ: x 2 = y + 3 1
Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.
Известно, что точка M 1 ( 1 , 3 ) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x 2 = y — 5 . Запишите каноническое уравнение первой прямой.
Решение
Для первой прямой можно определить направляющий вектор a → = 2 , — 5 . Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x — 1 2 = y — 3 — 5
Ответ: x — 1 2 = y — 3 — 5
Через точку M 1 ( — 1 , 6 ) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2 x — 4 y — 7 = 0 . Запишите каноническое уравнение первой прямой.
Решение
Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2 , 4 . Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:
x — ( — 1 ) 2 = y — 6 4 ⇔ x + 1 1 = y — 6 2
📸 Видео
Видеоурок "Приведение к каноническому виду"Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видамСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Привести квадратичную форму к каноническому видуСкачать
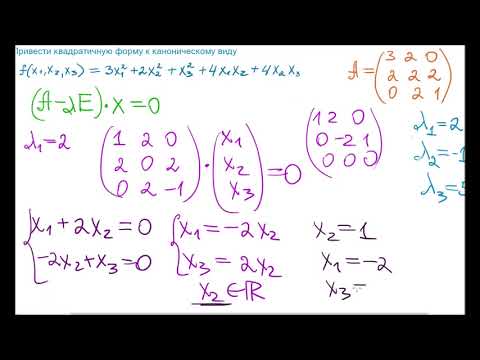
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

2. Приведение уравнений второго порядка к каноническому видуСкачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

§23 Приведение матрицы к каноническому видуСкачать

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертежСкачать