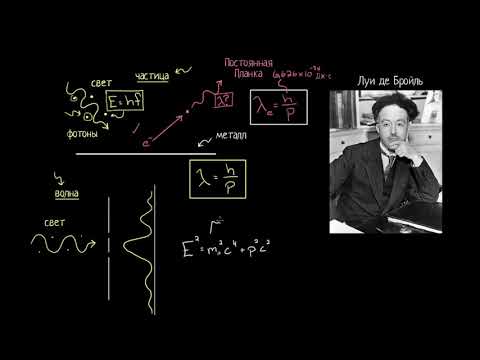
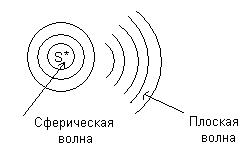
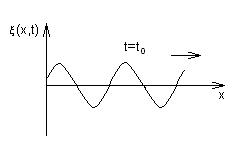
Пусть в точке О, которую примем за начало координат, находится источник колебаний, колеблющийся по закону x = A·cos wt, где x — мгновенное значение колеблющейся величины, А — амплитуда, w — циклическая частота. Рассмотрим процесс распространения колебаний, например, вдоль координатной оси Оx. Обозначим скорость распространения волны, т.е. скорость передвижения фронта волны, через u. Очевидно, что колебания в точке с координатой х начинаются через промежуток времени t = х/u, который необходим, чтобы колебания достигли этой точки. Тогда уравнение колебаний в данной точке описываются уравнением x = A·cos w(t – t) = A·cos w(t – х/u). Обычно это уравнение записывают в ином виде. Для этого преобразуем аргумент косинуса: w(t – х/u) = = wt – хw/u = wt – 2pх/(uT), так как w = 2p/T, где Т — период колебаний. Расстояние, на которое распространяется волна за период колебания, называется длиной волны. Обозначим её через l. Тогда uT = l. С учётом этого запишем:
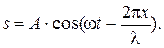
Уравнение (1) называется уравнением плоской монохроматической волны. В этом уравнении A и w ¾ амплитуда и циклическая частота волны, равная амплитуде и циклической частоте колебаний, происходящих в разных точках волны; 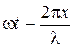
Звук представляет собой колебания воздуха или другой упругой среды, воспринимаемые нашими органами слуха. Звуковые колебания, воспринимаемые человеческим ухом, имеют частоты, лежащие в пределах от 20 до 20000 Гц. Колебания с частотами меньше 20 Гц называются инфразвуковыми, а больше 20 кГц — ультразвуковыми.
1. Характеристики звука. Звук у нас ассоциируется с его слуховым восприятием, с ощущениями, которые возникают в сознании человека. В связи с этим выделяют три его основные характеристики: высота, тембр и громкость звука.
а) Высота и тембр звука. Физической величиной, характеризующей высоту звука, является частота колебаний звуковой волны. Чем меньше частота, тем ниже звук, а чем больше частота, тем выше звук. Звук, издаваемый при полёте
жука, имеет частоту несколько десятков герц, тогда как писк комара — частоту, приближающуюся к 20000 Гц. Когда мы слышим музыкальный звук, то кроме высоты и громкости, мы воспринимаем его тембр. Звучание одной и той же ноты (следовательно, звучание одинаковой частоты) на скрипке и трубе чётко различаются на слух. Тембр звука связан с физически измеримыми величинами. Он определяется наличием обертонов (удвоенных, утроенных и т.д. частот основной частоты), их числом и амплитудами. У различных музыкальных инструментов число обертонов и их амплитуды оказываются различными. Именно это придаёт звуку каждого инструмента определённый тембр. Тембровая окраска звука определяется распределением интенсивностей обертонов, как, например, изображено на рис. 2. Другой тип звука — шум, который имеет место, например, при ударе двух камней друг о друга, ударе по всем клавишам рояля и т.д. Шум характеризуется большим числом частот, которые слабо связаны или не связаны друг с другом. Спектр шума представляет собой непрерывный набор частот и отдельные линии не выделяются.
б) Громкость звука. Громкость звука связана с физически измеряемой величиной — интенсивностью волны. Интенсивность равна энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению её распространения. Интенсивность звуковых волн очень низка. Она изменяется от 10 –12 (порог слышимости) до 10 Вт/м 2 (болевые ощущения). Так, энергия рёва большой толпы футбольных болельщиков, приветствующих гол, приблизительно равна внутренней энергии чашки кофе при температуре Человеческое ухо воспринимает невероятно широкий диапазон интенсивностей, крайние его значения различаются в 10 13 раз. Установлено, что величина, которую мы воспринимаем как громкость, не прямо пропорциональна интенсивности. Уровень громкости L вычисляется через интенсивность данного звука I по формуле где за I0 принимается величина порога слышимости, причём используется десятичный логарифм. Уровень громкости измеряется в белах (Б). Однако удобнее оказалось использовать величину в 10 раз меньшую — децибел. Значение в этом случае записывается Для примера приведём сравнительную таблицу уровней громкости (табл. 1). 1. Электромагнитные волны являются одним из наиболее важных типов волн, которые широко используются на практике. В отличие от механических волн для их распространения не нужно упругой среды. Они могут распространяться и в вакууме. Два фундаментальных закона природы лежат в основе существования электромагнитных волн: закон электромагнитной индукции Фарадея, согласно которому изменяющееся магнитное поле создаёт электрическое поле, и закон Максвелла, по которому переменное электрическое поле ответственно за возникновение магнитного поля. Возникшее в какой-либо точке пространства изменяющееся, например, магнитное поле порождает изменяющееся электрическое поле, которое, в свою очередь, вызывает появление переменного магнитного поля и т.д. Возникает электромагнитное поле, которое распространяется в пространстве. При этом в каждой точке пространства векторы напряжённости 2. Виды электромагнитных волн. Существованием электромагнитных волн объясняются многие явления, наблюдаемые в природе, которые часто не похожи друг на друга в своих проявлениях. Оказалось, что видимый свет, радиоволны, рентгеновские лучи, g-лучи имеют одну и ту же природу ¾ это электромагнитные волны, различающиеся только длиной волны. Электромагнитные волны в принципе могут иметь любую длину волны lu в вакууме (или частоту n, которая связана с lu соотношением n = с / lu , где с = 3×10 8 м/с ¾ скорость света в вакууме) от нуля до бесконечности. Весь диапазон длин волн можно приближённо разделить на ряд областей, каждая из которых связана с определённым видом излучения. Различные виды электромагнитных волн приведены в табл. 2, где приведены также приближённые значения частот и длин волн их
границ, поскольку соседние диапазоны перекрывают друг друга. Классификация различных видов электромагнитных волн, приведённая в таблице, основывается не только на их проявлениях, но и на способе их генерации. Электромагнитные волны с низкими частотами (n 3 Гц) генерируются переменными электрическими токами соответствующей частоты и не имеют практического значения. Радиоволны, используемые для радио и телепередач, генерируются при колебательных движениях зарядов в колебательном контуре, присоединённом к антенне. Инфракрасные (ИК) волны, диапазон которых примыкает к радиоволнам, возникают вследствие колебаний ионов кристаллических решёток, к которым подводится тепловая энергия (излучение ИК волн нагретой металлической спиралью в бытовом нагревательном рефлекторе). Очень узкий диапазон занимает видимый свет (от 400 до 750 нм). Электромагнитные колебания, невидимые человеческим глазом, с более высокими частотами создают ультрафиолетовое излучение. Видимый свет и ультрафиолетовое излучение генерируются возбуждёнными валентными электронами атомов за счёт энергии, подводимой извне (свечение газонаполненной трубки под действием электрического тока). Рентгеновское излучение возникает при резком торможении потока электронов препятствиями. Пульсации ядерного заряда приводят к созданию g-излучения. ВОЛНОВЫЕ СВОЙСТВА СВЕТА С точки зрения волновой теории свет представляет собой электромагнитные волны с частотой n, лежащей в интервале от 0,4×10 15 до 0,75×10 15 Гц. Диапазон световых волн чаще выражают в длинах волн в вакууме (практически в воздухе). Используя соотношение длины lu световой волны с частотой колебания (lu = c/n, где c = 3×10 8 м/с — скорость света в вакууме), находим, что длины волн света в вакууме заключены в пределах от 0,75 до 0,4 мкм. Установлено, что цветовое воздействие света на глаз человека обусловлено его частотой. Так, световые волны с частотой 0,4·10 15 Гц воспринимаются как красный свет, а с частотой 0,75·10 15 Гц — как фиолетовый. Показано также, что световые волны, отличающиеся по длине волны менее чем на 2 нм, воспринимаются как одноцветные. Интерференцией волн называют явление усиления и ослабления волн в определённых точках пространства при их наложении. Интерферировать могут только когерентные волны. Когерентными называются волны (источники), частоты которых одинаковы и разность фаз колебаний не зависит от времени. Геометрическое место точек, в которых происходит усиление или ослабление волн соответственно называют интерференционным максимумом или интерференционным минимумом, а их совокупность носит название интерференционной картины. В связи с этим можно дать иную формулировку явления. Интерференцией волн называется явление наложения когерентных волн с образованием интерференционной картины. Рассмотрим процесс наложения двух когерентных волн любой природы (механические, электромагнитные). Пусть эти волны создаются когерентными источниками O1 и O2, находящимися в одной среде, амплитуды и циклические частоты которых одинаковы и равны А и w, а начальные фазы равны нулю. Расстояние между источниками О1 и О2 намного меньше расстояний х1 и х2от источников до точки наблюдения М. Тогда волны от источников О1 и О2 распространяются практически параллельно, и вызываемые ими колебания в точке M (рис. 3) находим, используя уравнение плоской монохроматической волны (см. (1)): где x1 и x2 — мгновенные значения колеблющейся величины; l — длина волны в данной среде; x1 и x2 — расстояние от источников до точки наложения волн. Результирующее колебание s равно алгебраической сумме колебаний, обусловленных отдельными волнами, поскольку колебания происходят в одном направлении, т.е.
|








 Рис. 2
Рис. 2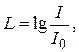 (2)
(2)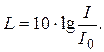 (3)
(3)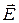 электрического поля и индукции
электрического поля и индукции  магнитного поля взаимно перпендикулярны и расположены в плоскости, перпендикулярной к направлению распространения волны.
магнитного поля взаимно перпендикулярны и расположены в плоскости, перпендикулярной к направлению распространения волны.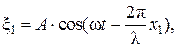
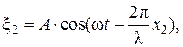 (4)
(4)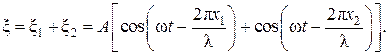 Используя соотношение
Используя соотношение 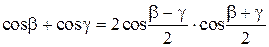 и полагая
и полагая 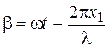 и
и  , получаем:
, получаем: 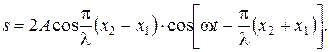 Выражение
Выражение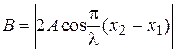 (5)
(5)



 Рис. 3
Рис. 3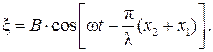 Таким образом, в произвольной точке М происходят гармонические колебания с той же циклической частотой w, амплитуда которых зависит от геометрической разности (х2 – х1) хода волн. Найдём условия усиления и ослабления колебаний в различных точках пространства. Очевидно, что амплитуда В результирующих колебаний будет максимальной в тех точках, для которых
Таким образом, в произвольной точке М происходят гармонические колебания с той же циклической частотой w, амплитуда которых зависит от геометрической разности (х2 – х1) хода волн. Найдём условия усиления и ослабления колебаний в различных точках пространства. Очевидно, что амплитуда В результирующих колебаний будет максимальной в тех точках, для которых 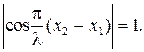 Это возможно, если
Это возможно, если 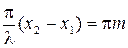 , где m = 0, ±1, ±2, ¼. Отсюда
, где m = 0, ±1, ±2, ¼. Отсюда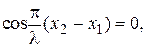 т.е. когда
т.е. когда 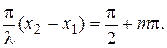 Отсюда
Отсюда















 Рис. 4
Рис. 4
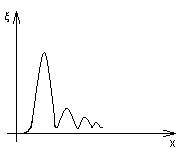
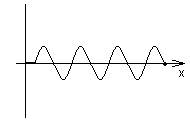 Цуг волны
Цуг волны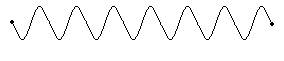
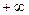
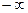
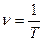 – частота
– частота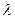 – длина волны – расстояние пройденное волной за 1 период
– длина волны – расстояние пройденное волной за 1 период