В состоянии физиологического покоя наружная и внутренняя стороны клеточной мембраны несут разноименные заряды. Поскольку носителями зарядов в биологических системах выступают ионы, то регистрируемая разность потенциалов обусловлена их неравновесной концентрацией на разных сторонах мембраны. Мембранная разность потенциалов рассчитывается по формуле Нернста:
где с1 и с2 – молярные концентрации ионов по обе стороны мембраны, R – универсальная газовая постоянная, Т – температура, Z – заряд иона, F – постоянная Фарадея.
Величина разности потенциалов для невозбужденной клетки составляет -50 ¸ -90 мВ и называется мембранным потенциалом покоя (ПП). Она обусловлена неравенством концентраций ионов (Na + , K + , Cl – ) внутри клетки и снаружи, а так же различной проницаемостью мембраны для этих ионов.
В настоящее время общепризнанной является мембранно-ионная теория возникновения ПП (Бернштейн, 1902; Ходжкин, Хаксли, Катц, 1949-1952). Этапы формирования ПП:
1. За счет работы Na + -K + -АТФ-азы создается повышенное содержание ионов Na + снаружи и ионов K + – внутри клетки.
2. Мембрана проницаема для K + и ионы начинают диффундировать из цитоплазмы в межклеточную жидкость по концентрационному градиенту, однако этот поток будет ограничен возникающим электрическим градиентом. Проницаемость мембраны для Na + значительно ниже:
поэтому ионы натрия скапливаются у наружной поверхности мембраны.
3. Диффузия ионов хлора из клетки не может компенсировать разность потенциалов, поскольку ограничена концентрационным градиентом. Для крупных органических анионов мембрана непроницаема и они скапливаются на ее внутренней поверхности.
Поскольку вклад в формирование ПП вносят различные ионы, результирующая величина разности потенциалов определяется по формуле Гольдмана–Ходжкина–Катца:

где i – внутри (internus), е – снаружи (externus), A – анионы.
При действии внешних стимулов клетки возбудимых тканей (нервная, мышечная, железистая) способны изменять мембранную разность потенциалов по величине и знаку. Подобная перезарядка мембраны получила название потенциала действия (ПД). ПД – электрический импульс, возникающий между внутренней и наружной сторонами мембраны и обусловленный изменением ее ионной проницаемости. Проницаемость мембраны для ионов в состоянии возбуждения составляет:
то есть для Na + возрастает в 500 раз по сравнению с уровнем физиологического покоя. Происходит быстрая диффузия Na + внутрь клетки, значительно превышающая скорость переноса соответствующих анионов. В результате переноса катиона происходит деполяризация мембраны (снижение существующей разности потенциалов до нуля) и последующая инверсия (смена заряда мембраны на противоположный). Затем происходит закрытие натриевых каналов и открытие калиевых. Ионы К + начинают выходить из клетки по концентрационному и электрическому градиентам, что приводит мембранный потенциал к исходному уровню (стадия реполяризации). Последующая работа Na + -K + -АТФ-азы восстанавливает ассиметричные концентрации катионов по обе стороны мембраны, характерные для ПП (рис. 7).
 |
| Рис. 7. Изменение мембранного потенциала при возбуждении |
Продолжительность ПД для большинства клеток составляет несколько миллисекунд.
Свойства потенциала действия:
1. Величина ПД не зависит от силы раздражителя (допороговые раздражители не приводят к его возникновению) – закон «все или ничего».
2. Возникает спустя латентный период (время достижения мембранным потенциалом критической величины).
3. После стадии реполяризации наступает период остаточной рефрактерности (невозбудимости мембраны).
4. Распространяется по мембране без ослабления на большие расстояния.
Таким способом возбуждение распространяется по безмякотным нервным волокнам. Для увеличения скорости и экономичности распространения нервных импульсов в процессе эволюции сформировались нервные волокна, покрытые изолирующей миелиновой оболочкой (рис. 8). ПД может возникнуть только на оголенных участках мембраны (перехваты Ранвье) и передача возбуждения носит сальтаторный (скачкообразный) характер. Генерация ПД в этом случае обусловлена не местными токами, а действием электрического поля, возникающего вокруг возбужденного участка мембраны. Скорость распространения нервных импульсов по безмиелиновым нервным волокнам »15 м/с, по миелиновым до 100 м/с.
Рис. 8. Строение миелинового нервного волокна
1. Дайте характеристику жидкокристаллической мозаичной модели строения биологической мембраны.
2. Охарактеризуйте подвижность липидов и белков в мембране.
3. Что такое фазовое состояние и фазовые переходы в мембранах?
4. Выделите основные функции биологических мембран.
5. По каким признакам транспорт веществ подразделяют на активный и пассивный?
6. Назовите основные пути проникновения молекул и ионов через мембрану.
7. Каковы основные механизмы пассивного транспорта?
8. Как функционируют подвижные переносчики и каналообразователи?
9. Какие процессы в биологической системе обеспечиваются процессами фильтрации и реабсорбции?
10. Как влияет на соотношение процессов фильтрации и реабсорбции концентрация белка в сыворотке крови и тканевой жидкости?
11. Что называют вторично активным транспортом?
12. Объясните механизм возникновения и биологическую роль потенциала покоя?
13. Какие процессы в биомембране происходят при реализации потенциала действия? Как изменяется транспорт ионов через мембрану?
14. Дайте характеристику основным механизмам распространения нервного импульса по волокнам.
ПРИМЕРЫ ЗАДАНИЙ ДЛЯ КОМПЬЮТЕРНОГО ТЕСТИРОВАНИЯ
В основе плазматической мембраны лежит
а) углеводный каркас;
б) бислой липидов;
в) белковая матрица;
г) гликолипидная сетка.
Приведенная формула может быть использована для расчета переноса через мембрану
а) только нейтральных молекул;
б) нейтральных молекул и ионов при наличии на мембране только концентрационного градиента;
в) только ионов при наличии на мембране электрохимических градиентов;
г) нейтральных молекул и ионов при наличии на мембране электрохимических градиентов.
Наиболее вероятный способ переноса гидрофобного вещества при наличии концентрационного градиента –
а) активный транспорт;
б) диффузия через белковый канал;
в) диффузия через мембранную пору;
г) диффузия через липидную фазу.
Истощение в клетке запасов АТФ приведет к снижению интенсивности
а) облегченной диффузии;
в) активного транспорта;
г) активного транспорта и облегченной диффузии.
Уравнение Нернста позволяет определить
а) мембранный потенциал клетки;
б) подвижность ионов;
в) плотность потока ионов;
г) величину порогового раздражителя для мембраны.
1. Контроль исходного уровня знаний (компьютерное тестирование или иные формы).
2. Разбор теоретического материала занятия, коррекция усвоенного материала (устно-речевой контроль).
3. Решение типовых задач по теме занятия. Обсуждение алгоритма решения и практического значения расчетов скорости переноса веществ через биомембрану и величин биопотенциалов.
4. Изложение и обсуждение реферативных докладов. Обсуждение ситуационных задач.
5. Контроль конечного уровня знаний – работа с программой компьютерного тестирования по теме «Биофизика клетки».
6. Задание на следующее занятие с выделением материала для самостоятельной работы. Согласование тем реферативных докладов.
Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

Перенос молекул (атомов) через мембраны. Уравнение Фика
Важной характеристикой мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Вероятность такого проникновения зависит как от направления перемещения частиц (в клетку или из клетки), так и от разновидности молекул и ионов.
Эти вопросы относятся к явлениям переноса. Таким термином называют самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.
Рассмотрим наиболее существенные для биологических мембран явления: перенос вещества (диффузию) и перенос заряда (электропроводность).
Как синоним переноса частиц в биофизике используется термин «транспорт частиц».
Основное уравнение диффузии имеет вид
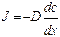
где J -плотность потока частиц, 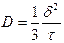
(1) называется уравнением Фика.
Уравнение Фика описывает диффузию в однородной среде. Модифицируем его для случая диффузии через мембрану. Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества. Например, если в сосуд, в котором поверх воды налито масло, бросить соль, то ее концентрации в этих средах будут различны.
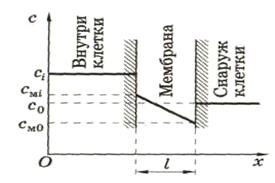
Пусть концентрация частиц, диффундирующих через мембрану, изменяется в мембране линейно (рис.11).
Рис.11. Распределение концентрации частиц, проходящих через мембрану
где 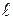
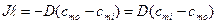
Практически легче определять концентрации частиц не внутри мембраны (cmi и cmo), а вне мембраны: в клетке (сi) и снаружи клетки (co). Предположим, что
где k -коэффициент распределения частиц между мембраной и окружающей средой. Тогда cmo = kco, cmi = kci , и имеем
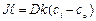
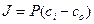
где 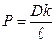
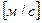
Перенос заряженных частиц. Электродиффузное уравнение Нернста-Планка
На мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле, которое влияет на диффузию заряженных частиц (ионов и электронов).
Плотность потока заряда дается выражением
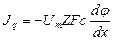
где φ – потенциал поля, F=eNA -постоянная Фарадея, Z – валентность, Um – подвижность диффундирующих частиц для одного моля.
В общем случае перенос ионов зависит от неравномерности их распределения и воздействия электрического поля. Суммарная плотность потока частиц определяется электродиффузным уравнением Нернста-Планка
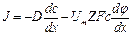
Для нейтральных частиц (Z=0) уравнение Нернста-Планка переходит в уравнение Фика.
Видео:Физическая кинетика. Часть 2. Явление переноса. Диффузия.Скачать

Лекция 5, 6. Биофизика транспортных процессов
Лекция 5, 6. Биофизика транспортных процессов
Перейдем теперь к рассмотрению некоторых направлений клеточной биофизики и начнем с биофизики транспортных процессов.
Прежде всего, определим некоторые понятия – под транспортом на клеточном ровне понимаются прежде процессы переноса нейтральных веществ и ионов через биологические мембраны, и именно эти процессы изучаются в первую очередь в биофизике транспортных процессов. Надо отметить, что транспорт на клеточном уровне этими процессами не исчерпывается. Так существует латеральный транспорт – т. е. транспорт веществ ВДОЛЬ мембраны. Можно говорить также о транспорте веществ внутри клетки, который не связан с мембранными структурами, а осуществляется, например, за счет взаимодействия транспортируемых молекул с белками цитоскелета или водных потоков внутри клетки.
Однако именно трансмембранный транспорт, т. е. транспорт ЧЕРЕЗ биологические мембраны играет одну из ключевых ролей. Поему так? Чтобы понять это, необходимо вспомнить роль биологических мембран в существовании живых систем.
Как вы, наверно, знаете мембраны представляют собой клеточные структуры состоящие из бислоя (если нужно – напомнить структуру бислоя, РИС) и взаимодействующих с ним белков. У прокариот основной мембранной структурой является клеточная мембрана, выполняющая широкий спектр функций. У эукариот имеется широкий спектр мембранных структур – плазматическая мембрана, ядерная мембрана, сопрягающие мембраны – у митохондриальная и тилакоидная, и другие. Наиболее общей функцией биомембран является барьерная – т. к. за счет центрального гидрофобного участка в бислое, они обладают очень низкой проницаемостью для полярных, водорастворимых соединений. Именно благодаря этой функции мембраны и стали играть столь значительную роль в функционировании живых систем – без них само существование живых систем как отдельных объектов стало бы невозможным.
Однако, как мы уже говорили, живые системы – это открытые системы, т. е. системы, которые не могут существовать без обмена с внешней средой веществом и энергией. Отсюда существование биомембран, являющееся само по себе необходимым условиям для существования живых организмов в том виде в каком они есть, с необходимостью требует существования транспортных процессов через эти мембраны и обуславливает большую биологическую значимость этих процессов.
Рассмотрим процессы транспорта через биомембраны подробнее.
Простая диффузия представляет собой движение молекул незаряженного вещества по градиенту концентрации, т. е. от участков с более высоким содержанием данного вещества к участкам с более низким содержанием его. Такой процесс является пассивным, т. е. его непосредственное протекание не требует затрат энергии. Его существование было изначально показано эмпирически, однако этот закон может быть выведен, например, из более общего второго принципа термодинамики (равновесие – как отсутствие градиентов, если нужно объяснить). Впрочем, к явлению диффузии легко прийти и на основе молекулярной картины строения вещества и броуновского движения, которое, в общем-то, тоже вытекает из этой картины. Так, если у нас имеется два отсека, заполненных, например, разной концентрацией газа, то если мы откроем перегородку между этими отсеками, то получим, что количество молекул, движущихся из 1 в 2, будет пропорционально концентрации газа в 1, а из 2 в 1 – концентрации газа в 2 (РИС). Т. е. можно записать, что 




Отметим, что D – коэффициент диффузии, размерность которого обычно см2*с-1, j – поток вещества, с размерностью М*см-2*с-1. D – можно найти, учитывая, что 
В том случае, когда речь идет о перемещении вещества через тонкий барьер, например, через биомембрану, толщиной h, можно принять внутри этого барьера связь между С и х имеет линейный характер, т. е. dC/dx = const. Справедливость этого легко доказать, проанализировав зависимость ΔС от x, на участке от 0 до h:

 | Дорожное хозяйство России строительство и содержание дорог — это очень важно |
| |
Видео:27. Уравнения переносаСкачать

 Транспорт
Транспорт
💡 Видео
Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

10.3 Закон Фика и уравнение диффузии моноэнергетических нейтронов (часть 3)Скачать

Уравнение с модулемСкачать

2 5 Граничные условия для диффузионного уравненияСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Химия | Молекулярные и ионные уравненияСкачать

Закон диффузии ФикаСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Расчеты по уравнениям химических реакций. 2 часть. 8 класс.Скачать

6-2. Метод сетокСкачать

2 3 Вывод диффузионного уравненияСкачать

Диффузия и осмос (видео 6) | Мембранный транспорт| БиологияСкачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Решение неоднородного рекуррентного уравненияСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать



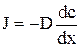
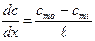
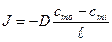
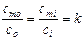
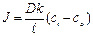

 Транспорт
Транспорт