Приведение уравнения поверхности второго порядка к каноническому виду методом собственных векторов

Любой матрице A порядка N соответствует линейный оператор j в пространстве R N, заданный формулой j(X) = AX. Справедлива теорема.

Теорема 1. Для любой симметрической матрицы A порядка N в пространстве R N имеется ортонормированный базис, состоящий из собственных векторов матрицы А.

Алгоритм построения ортонормированного базиса.

1. Составить характеристическое уравнение матрицы det(A— LE) = 0 и найти все собственные значения матрицы A.

2. Для каждого собственного значения составить систему однородных линейных уравнений (A— LE)X = 0 и найдем фундаментальную систему решений и ортогонализуем ее.

3. Объединяем все полученные ортогональные системы и нормируем полученный базис. Получим ортонормированный базис, состоящий из собственных векторов матрицы А.

Пример. Найти ортонормированный базис пространства, состоящий из собственных векторов матрицы .

1. Составить характеристическое уравнение матрицы и найдем все собственные значения матрицы A

.

2. Найдем собственные векторы, решая системы уравнений:

,,,

Общее решение первой системы (0, 0, X3 ), фундаментальное решение (0, 0, 1).

Общее решение второй системы (X2, X2, 0 ), фундаментальное решение (1, 1, 0).

Общее решение третьей системы (-X2, X2, 0 ), фундаментальное решение (-1, 1, 0).

Ортогонализовать в данном случае не нужно, так как каждая фундаментальная система решений состоит из одного вектора.

3. Объединяя и нормируя, полученные векторы получим ортонормированный базис пространства, состоящий из собственных векторов матрицы А: .

Отсюда получаем алгоритм приведения квадратичной формы к каноническому виду:

1. Составить матрицу квадратичной формы.

2. Составить характеристическое уравнение матрицы det(A— LE) = 0 и найти все собственные значения L1, L2, . LN матрицы A.

3. Составить квадратичную форму канонического вида F = (при необходимости методом, указанным выше, можно найти канонический базис, в котором квадратичная форма имеет канонический вид.

Пример. Квадратичная форма F(X1, X2, x3) = в силу предыдущего примера имеет канонический вид

F = канонический базис .

Рассмотрим преобразование общей поверхности s второго порядка, заданной уравнением (1) к частным случаям.

1. Выполним ортогональное преобразование поверхности s, при котором квадратичная форма перейдет в квадратичную форму канонического вида , где все собственные значения L1, L2, . LN матрицы A =(Aij). При этом поверхность s в новой системе координат OY1Y2Y3 будет иметь уравнение

. (22)

2. Если LI ≠ 0, то соответствующий линейный член A’i в уравнении (2) можно исключить, выполнив преобразование по формулам , если LI ≠ 0, и Zi = Yi, если LI = 0. Уравнение поверхности s примет вид:

. (23)

Теперь возможны случаи.

1) Все A‘I = 0 и B« = 0. Тогда уравнение (23) поверхности s представим в виде: . Это поверхность видов 2, 6, 10, 13, 17.

2) Все A‘I = 0 и B« ≠ 0. Тогда уравнение (23) поверхности s представим в виде: . Это поверхность видов 1, 3, 4, 5, 9, 11, 12, 15.

2) В (3) найдется A‘J ≠ 0. ви B« ≠ 0. Тогда выполнив преобразование (23) по формулам , Wi = Yi, если I ≠J. Уравнение поверхности s примет вид: .

Это поверхность видов 7, 8, 14.

Пример 2. Определим вид поверхности, определяемой уравнением

.

В силу примера в предыдущем параграфе квадратичная форма поверхности имеет канонический вид F = в каноническом базисе . Напишем преобразования координат

.

После этого уравнение поверхности примет вид:

Выделим полный квадрат , и выполним преобразование переменных по формулам: и получим

.

Разделим обе части на 9/8 получим уравнение

Пример 1. Определим вид кривой, определяемой уравнением .

Рассмотрим квадратичную форму кривой , и приведем ее к каноническому виду. Составим

Характеристическое уравнение кривой и найдем собственные значения и собственные векторы.

.

Составим векторные уравнения, для нахождения собственных векторов

.

Тогда квадратичная форма поверхности имеет канонический вид F = в каноническом базисе, . Напишем преобразования координат . После этого уравнение поверхности примет вид: Выделим полный квадрат , и выполним преобразование переменных по формулам:

И получим . Разделим обе части на 17/5 получим уравнение гиперболы.

.

Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Написать реферат

Пусть в пространстве задана прямоугольная декартова система координат . Рассмотрим общее уравнение поверхности второго порядка, коэффициенты в котором обозначены специальным образом

где — числа, причем хотя бы одно из чисел отлично от нуля.

Выделим квадратичную часть выражения, стоящего в уравнении слева,

Определить вид кривой . Примеры решения и оформления задач контрольной работы

Такое выражение называется квадратичной формой от трех переменных . Составим матрицу

Эта матрица называется матрицей квадратичной формы . Она является симметричной , то есть , или, другими словами, . Следует обратить внимание на то, как эта матрица составлена. На диагонали у нее стоят коэффициенты при квадратах переменных, а в остальных местах — половины коэффициентов при произведениях переменных.

Исходная система координат является прямоугольной, поэтому скалярное произведение векторов с координатными столбцами , задается формулой . Сформулируем две теоремы, позволяющие пользоваться приведенным ниже алгоритмом.

Пусть — матрица квадратичной формы . По сформулированной теореме у нее существует ортонормированный базис из собственных векторов. Обозначим их , , , и пусть эти векторы имеют координаты

Базис i , j , k назовем старым, а базис — новым. Тогда матрица перехода 19.1.4.а будет иметь вид

Выберем новую систему координат так, что начало координат не изменяется, а новые базисные векторы , , задают направления новых координатных осей , , (рис. 19.8).

Тогда координаты точки являются координатами ее радиус-вектора и, следовательно, при замене базиса меняются по формуле (18.1)

Если мы из равенства (19.8) выпишем выражение , , через новые переменные , , и подставим в уравнение (19.7), то обнаружим, что квадратичная его часть и линейная часть преобразуются независимо друг от друга. В результате уравнение в системе координат имеет вид

Хотя бы одно из чисел , , отлично от нуля, иначе матрица была бы нулевой.

Рассмотрим три случая.

Пусть все собственные числа , , отличны от нуля. В уравнении (19.9) выделим полные квадраты

Выполним параллельный перенос системы координат , взяв за новое начало системы координат точку (см. формулы (13.21)). Тогда в новой системе координат уравнение запишется в виде

Здесь возможны следующие варианты.

Пусть . Перенесем в правую часть и поделим обе части на , получим

1. Если числа , , отрицательны, то ни одна точка пространства не удовлетворяет этому уравнению. Говорят, что оно определяет мнимый эллипсоид .
2. Если числа , , положительны, то уравнение является каноническим уравнением эллипсоида.
3. Если одно из чисел , , отрицательно, а остальные положительны, то (после переименования осей) получим каноническое уравнение однополостного гиперболоида.
4. Если одно из чисел , , положительно, остальные отрицательны, то (после переименования осей) получим каноническое уравнение двуполостного гиперболоида.

Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.

к каноническому виду.

Решение. Квадратичная форма имеет вид

Выписываем ее матрицу

Находим ее собственные числа. Для этого запишем характеристическое уравнение

После вычисления определителя получим

Подбором находим один корень . Преобразуем уравнение, выделяя множитель

Находим два других корня характеристического уравнения и .

Находим собственные векторы. Для собственного числа для координат собственного вектора получим систему уравнений

Решая ее находим, что фундаментальная система решений содержит только одно решение, и в качестве собственного вектора можно взять . Для собственного числа для координат собственного вектора получим систему уравнений

Отсюда находим собственный вектор . Для собственного числа для координат собственного вектора получим систему уравнений

Отсюда находим собственный вектор .

Легко проверить, что , то есть собственные векторы попарно ортогональны. Их длины равны соответственно , , . Поэтому векторы нового ортонормированного базиса будут иметь координаты

Матрица перехода имеет вид

Старые координаты связаны с новыми уравнением , то есть

Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа

Приводим подобные члены

Выделим полные квадраты

Выполняем параллельный перенос осей координат

Новое начало системы координат имеет координаты

В исходной системе координат точка в соответствии с формулами (19.10) имеет координаты

Рис. 19 . 9 .Система координат

В новой системе координат (рис. 19.9) уравнение принимает канонический вид

Это уравнение является каноническим уравнением однополостного гиперболоида. Его центр находится в точке , две вещественные оси параллельны векторам , , вещественные полуоси равны , . Мнимая ось параллельна вектору , мнимая полуось равна . Изображение гиперболоида приведено на рисунке 19.10.

Рис. 19 . 10 .Изображение гиперболоида

Задачи, приводящие к дифференциальным уравнениям. Обыкновенное дифференциальное уравнения (ОДУ). Интегрирование в квадратурах. Фазовое пространство. Изоклины. Интегральная кривая. Задача Коши для ОДУ. Теорема существования и единственности решения задачи Коши. Общее и частное решения. ОДУ высших порядков. Понижение порядка. Краевая задача. Однородное и неоднородное ОДУ, принцип суперпозиции решений. Фундаментальная система решений, определитель Вронского. Метод Лагранжа вариации произвольных постоянных. Построение фундаментальной системы решений по корням характеристического уравнения. Системы ОДУ.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Поверхности второго порядка: их виды, уравнения, примеры

Видео:Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

.

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

.

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

.

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

,

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

,

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

.

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

.

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

.

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

,

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

.

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

,

,

получим каноническое уравнение эллиптического параболоида:

.

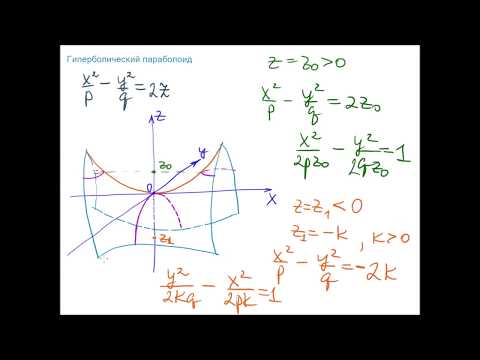
Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

.

, ,

получим каноническое уравнение гиперболического параболоида:

.

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение эллиптического цилиндра:

.

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

.

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

.

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, пересекающихся плоскостей:

.

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

,

.

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

.

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

.

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

,

перепишем его в виде

.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

,

перепишем его в виде

.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

.

Видео:Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать

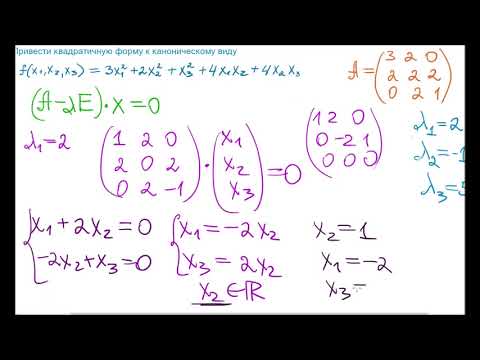
Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

(как вычислить определитель).

I 1 = 1 + 5 + 1 = 7 ,

Следовательно, данная поверхность — однополостный гиперболоид.

.

Составляем и решаем характеристическое уравнение:

;

.

,

, , .

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

.

.

Следовательно, общее уравнение определяет эллиптический параболоид.

.

I 1 = 2 + 2 + 3 = 7 .

Решаем характеристическое уравнение:

.

.

,

, .

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

,

,

,

I 1 = 5 + 2 + 5 = 12 .

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

.

.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

🎦 Видео

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Привести квадратичную форму к каноническому видуСкачать

Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Приведение кривой второго порядка к каноническому виду. ТемаСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Видеоурок "Приведение к каноническому виду"Скачать

Лекция 7. Приведение общего уравнения кривой второго порядка к каноническому видуСкачать

Поворот и параллельный перенос координатных осей. ЭллипсСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядкаСкачать

Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать