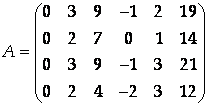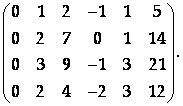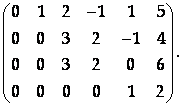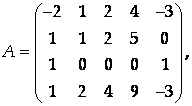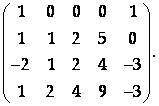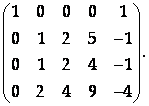Приведение матрицы уравнений к ступенчатому виду

Видео:Приведение матрицы к ступенчатому виду. Алгоритм ГауссаСкачать

Приведенные ступенчатые матрицы

Этот онлайн калькулятор преобразует заданную матрицу к приведенному ступенчатому виду по строкам (каноническому виду по строкам) и показывает решение по шагам.

Этот онлайн калькулятор проводит пошаговое преобразование заданной матрицы к приведенному ступенчатому виду. Помимо решения — приведенной ступенчатой матрицы — калькулятор также показывает использованные на каждом шаге элементарные преобразования строк. Определения терминов, для тех, кто забыл, приведены, как обычно, под калькулятором.

Приведенные ступенчатые матрицы

Ступенчатая матрица

Ступенчатой матрицей, или матрицей ступенчатого вида по строкам, называется матрица, такая что

• все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками
• ведущий элемент (первый, считая слева направо, ненулевой элемент строки) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

Примеры ступенчатых матриц:

• нулевая матрица
• однострочная матрица
• единичная матрица
• верхнетреугольная матрица

Матрица, приведенная ниже, также является ступенчатой матрицей:

Приведенная ступенчатая матрица

Ступенчатая матрица называется приведенной, если матрица, составленная из всех ее основных столбцов, является единичной матрицей (столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы).

То есть, приведенная ступенчатая матрица не имеет нулевых строк, и все ведущие элементы ее строк равны единице. При этом все элементы основных столбцов, помимо ведущих элементов, являются нулями.

Матрица, приведенная ниже, является приведенной ступенчатой матрицей:

Преобразование матрицы к приведенному ступенчатому виду по строкам (каноническому виду по строкам)

Для приведения матрицы к ступенчатому или приведенному ступенчатому виду используются элементарные преобразования строк. Каждая матрица может быть преобразована к уникальному приведенному ступенчатому виду.

Элементарные преобразования строк:

• перестановка местами любых двух строк матрицы

• умножение любой строки матрицы на ненулевую константу

• прибавление к любой строке матрицы другой строки, умноженной на некоторую ненулевую константу

Эти преобразования и используются калькулятором выше для приведения матрицы к каноническому виду по строкам.

Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Метод Гаусса приведения матрицы к ступенчатому виду

Элементарными преобразованиями матрицы называются следующие ее преобразования:

I. Перестановка двух столбцов (строк) матрицы.

II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.

III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

Матрица , полученная из исходной матрицы конечным числом элементарных преобразований, называется эквивалентной . Это обозначается .

Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач.

Покажем, как при помощи элементарных преобразований можно привести матрицу к ступенчатому виду (рис. 1.4). Здесь высота каждой «ступеньки» составляет одну строку, символом 1 (единицей) обозначены единичные элементы матрицы, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. К ступенчатому виду можно привести любую матрицу, причем достаточно использовать только элементарные преобразования строк матрицы .

Видео:Приведение матрицы к ступенчатому видуСкачать

Алгоритм приведения матрицы к ступенчатому виду

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля ( ведущий элемент ). Строку с ведущим элементом ( ведущая строка ), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

Пример 1.29. Привести к ступенчатому виду матрицы

Решение. В первом столбце матрицы выбираем ведущий элемент . Делим все элементы первой строки на (или, что то же 1 1. самое, умножаем на ):

Прибавим ко второй строке первую, умноженную на (-2):

Первый столбец и первую строку исключаем из рассмотрения. В оставшейся части матрицы имеется один элемент (-2), который выбираем в качестве ведущего. Разделив последнюю строку на ведущий элемент, получаем матрицу ступенчатого вида

Преобразования закончены, так как ведущая строка последняя. Заметим, что получившаяся матрица является верхней треугольной.

В первом столбце матрицы выбираем ведущий элемент . Меняем местами строки, ставя ведущую строку на место первой, и делим элементы ведущей строки на ведущий элемент 2:

Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит нуль. Исключаем из рассмотрения первую строку и первый столбец. В оставшейся части ведущий элемент — число 2. Разделив ведущую строку (вторую) на 2, получаем ступенчатый вид:

Преобразования закончены, так как ведущая строка последняя.

В первом столбце матрицы выбираем ведущий элемент . Первая строка — ведущая. Делим ее элементы на . Получаем

Ко второй и третьей строкам прибавим первую, умноженную на (-3) и на (-6) соответственно:

Обратим внимание на то, что полученная матрица еще не является матрицей ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и 3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части ведущий элемент. Это элемент (-1). Делим вторую строку на (-1), а затем к третьей строке прибавляем ведущую (вторую), умноженную на 5:

Исключим из рассмотрения вторую строку и второй столбец. Поскольку исключены все столбцы, дальнейшие преобразования невозможны. Полученный вид — ступенчатый.

1. Говорят, что матрица имеет ступенчатый вид также и в случае, когда на месте ведущих элементов (обозначенных на рис. 1.4 единицей) стоят любые отличные от нуля числа.

2. Считается, что нулевая матрица имеет ступенчатый вид.

Пример 1.30. Привести к ступенчатому виду матрицу

Решение. Первый столбец матрицы — нулевой. Исключаем его из рассмотрения и исследуем оставшуюся часть (последние 5 столбцов):

Берем в качестве ведущего элемент . Прибавляем ко второй строке первую, умноженную на (-1); к третьей строке — первую, умноженную на (-2); к четвертой строке — первую, умноженную на (-4). Тем самым «обнуляются» все элементы второго столбца, расположенные ниже ведущего элемента:

Полученная матрица не имеет ступенчатого вида, так как одна из ступенек имеет высоту в три строки. Продолжаем преобразования. Первую строку и второй столбец исключаем из рассмотрения. Поскольку первый столбец в оставшейся части матрицы нулевой, исключаем его. Теперь оставшаяся часть матрицы — это матрица (размеров ), образованная элементами, расположенными в последних трех строках и трех столбцах полученной матрицы. В качестве ведущего элемента выбираем . К третьей строке прибавляем вторую. Получаем матрицу

Вторую строку и четвертый столбец исключаем из рассмотрения. Берем элемент в качестве ведущего. Делим третью строку на число 2 (умножаем на 0,5):

К четвертой строке прибавляем третью, умноженную на (-2):

Третью строку и четвертый столбец исключаем из рассмотрения. Поскольку в оставшейся части матрицы все элементы (один) нулевые, преобразования закончены. Матрица приведена к ступенчатому виду (см. рис. 1.4).

Замечание 1.9. Продолжая выполнять элементарные преобразования над строками матрицы, можно упростить ступенчатый вид, а именно привести матрицу к упрощенному виду (рис. 1.5).

Здесь символом 1 обозначены элементы матрицы, равные единице, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. Заметим, что в каждом столбце с единицей остальные элементы равны нулю.

Пример 1.31. Привести к упрощенному виду матрицу

Решение. Матрица имеет ступенчатый вид. Прибавим к первой строке третью, умноженную на (-1), а ко второй строке третью, умноженную на (-2):

Теперь к первой строке прибавим вторую, умноженную на (-1). Получим матрицу упрощенного вида (см. рис. 1.5):

Замечание 1.10. При помощи элементарных преобразований (строк и столбцов) любую матрицу можно привести к простейшему виду (рис. 1.6).

Левый верхний угол матрицы представляет собой единичную матрицу порядка , а остальные элементы равны нулю. Считается, что нулевая матрица уже имеет простейший вид (при ).

Пример 1.32. Привести матрицу к простейшему виду.

Решение. В качестве ведущего элемента возьмем . Ко второй строке прибавим первую, умноженную на (-2):

Ко второму столбцу прибавим первый, умноженный на (-2), а к третьему -первый, умноженный на (-3):

Умножим все элементы последнего столбца на (-1) и переставим его на место второго:

Таким образом, исходная матрица при помощи элементарных преобразований приведена к простейшему виду (см. рис. 1.6).

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Свойства элементарных преобразований матриц

Подчеркнем следующие свойства элементарных преобразований матриц .

Теорема 1.1 о приведении матрицы к ступенчатому виду . Любую матрицу при помощи элементарных преобразований ее строк можно привести к ступенчатому (или даже упрощенному) виду.

Следствие (о приведении матрицы к простейшему виду). Любую матрицу при помощи элементарных преобразований ее строк и столбцов можно привести к простейшему виду.

1. Преобразования, обратные к элементарным, являются элементарными . В самом деле, если в матрице поменяли местами два столбца (преобразование I типа), то исходную матрицу можно получить, еще раз поменяв местами эти столбцы. Если столбец матрицы умножили на число (преобразование II типа), то для получения исходной матрицы надо этот столбец умножить на обратное число . Если к i-му столбцу матрицы прибавили j-й столбец, умноженный на число , то для получения исходной матрицы достаточно к i-му столбцу матрицы прибавить j-й столбец, умноженный на противоположное число ( ).

2. В теореме 1.1 говорится о приведении матрицы к ступенчатому (упрощенному) виду при помощи элементарных преобразований только ее строк, не используя преобразования ее столбцов. Чтобы привести произвольную матрицу к простейшему виду (следствие теоремы 1.1), нужно использовать преобразования и строк, и столбцов матрицы.

3. Рассмотрим следующую модификацию пункта 3 метода Гаусса. Ведущий элемент, выбранный в п. 1 метода Гаусса, определяет ведущую строку и ведущий столбец матрицы (он находится на их пересечении). Делим все элементы ведущей строки на ведущий элемент (см. п.2 метода Гаусса). Прибавляя ведущую строку, умноженную на соответствующие числа, к остальным строкам матрицы (аналогично п.3 метода Гаусса), делаем равными нулю все элементы ведущего столбца, за исключением ведущего элемента. Затем, прибавляя полученный ведущий столбец, умноженный на соответствующие числа, к остальным столбцам матрицы, делаем равными нулю все элементы ведущей строки, за исключением ведущего элемента. При этом получаем ведущие строку и столбец, все элементы которых равны нулю, за исключением ведущего элемента, равного единице.

Модифицированный таким образом метод Гаусса называется методом Гаусса-Жордана . Его применение позволяет сразу получить простейший вид матрицы, минуя ее ступенчатый вид.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

2.2.3. Приведение матрицы к ступенчатому виду

Пусть дана ненулевая матрица

Опишем алгоритм, который с помощью элементарных преобразований приводит матрицу А к некоторому более простому виду. Будем использовать только элементарные преобразования строк, чтобы в дальнейшем можно было применить тот же алгоритм к решению систем линейных алгебраических уравнений.

Найдем в матрице А ненулевой элемент Ai1J1 c минимальным номером столбца J1 и переставим I1-ую строку с первой. Тогда получим матрицу вида

Теперь будем прибавлять к каждой строке с номером I, I = 2. M первую строку, умноженную на число 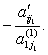В результате этих преобразований получим матрицу вида

Далее, с матрицей

Проведем преобразования, аналогичные тем, которые делались с исходной матрицей. Тогда исходная матрица будет приведена к виду

Продолжая этот процесс, придем к матрице Ступенчатого Вида

Для такой матрицы легко найти ранг. Действительно, выбрав первые R строк и столбцы J1, . Jr, получим минор

С другой стороны, любой минор порядка большего, чем R, равен нулю, так как содержит ненулевую строку. Тем самым ранг полученной матрицы равен R, а в силу того, что элементарные преобразования не меняют ранга матрицы, ранг исходной матрицы тоже равен R.

Приведем к ступенчатому виду матрицу

И найдем ее ранг. Чтобы иметь дело с целыми числами, удобно иметь ненулевой элемент с минимальным номером столбца равным единице. Для этого вычтем из первой строки вторую:

Теперь будем вычитать из всех строк, начиная со второй, первую, умноженную на элемент, стоящий во втором столбце и соответствующей строке:

Вычтем из третьей строки вторую:

Вычитая из последней строки третью, приходим к ступенчатому виду:

В полученной матрице три ненулевых строки, поэтому ее ранг, а значит, и ранг исходной матрицы равен 3.

Найти ранг матрицы

Приведя ее к ступенчатому виду.

Поменяем местами 1-ую и 3-ю строки матрицы А:

Теперь вычтем 1-ую строку из 2-ой и 4-ой, а к 3-ей строке прибавим 1-ую, умноженную на 2:

Вычтем из 3-ей строки 2-ую, а из 4-ой – удвоенную 2-ую:

Поменяем местами 3-й и 4-й столбцы и вычтем из последней строки 3-ю:

Вычислим минор 4-го порядка из столбцов 1,2,3 и 5:

🔥 Видео

Алгоритм приведения матрицы к треугольному видуСкачать

Приведение определителя к треугольному видуСкачать

MathCad приведение матрицы к ступенчатому виду.wmvСкачать

11. Ранг матрицыСкачать

Метод Гаусса. Элементарные преобразования. Ранг матрицы. Ступенчатая матрица. Эквивалентная матрицаСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Приведение матрицы к треугольному видуСкачать

§16 Приведение определителей к треугольному видуСкачать

§23 Приведение матрицы к каноническому видуСкачать

Ранг матрицыСкачать

Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Определитель 5 порядка приводим к треугольному видуСкачать

Решение системы уравнений методом ГауссаСкачать

5. Вычисление определителя методом приведения матрицы определителя к треугольному видуСкачать

Ранг матрицыСкачать