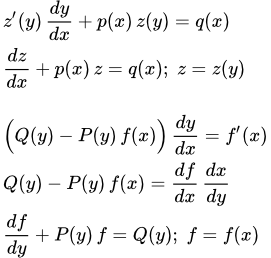Приведение к уравнений к линейным (7 видео)

Дифференциальные уравнения первого порядка, приводящиеся к линейным

Содержание

Метод решения
Дифференциальные уравнения, линейные относительно переменной x
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Приведение к каноническому виду линейных уравнений с частными производными второго порядка
ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ
🔥 Видео

Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

Метод решения

К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.

Видео:Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Дифференциальные уравнения, линейные относительно переменной x

Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .

Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка

Решить уравнение:
(П.1) .

Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:

;

;
;
.
Переходим к переменной x :
;
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Приведение к каноническому виду линейных уравнений с частными производными второго порядка

Федеральное агентство по образованию

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики, экономики и информатики

Кафедра дифференциальных и интегральных уравнений

ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………

1.1. Необходимый теоретический материал………………………..

1.2. Пример выполнения задачи1 (приведение к

каноническому виду уравнений гиперболического типа) .

1.3. Пример выполнения задачи 2 (приведение к

каноническому виду уравнений параболического типа)

1.4. Пример выполнения задачи 3 (приведение к

каноническому виду уравнений эллиптического типа) ..

1.5. Задачи для самостоятельного решения ………………….….

Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2.1. Необходимый теоретический материал …………………..

2.2. Пример выполнения задачи 4

2.3. Задачи для самостоятельного решения ……………………..

В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.

Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.

§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.

Задача. Определить тип уравнения

(1)

и привести его к каноническому виду.

1.1. Необходимый теоретический материал.

I. Тип уравнения (1) определяется знаком выражения :

· если в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.

Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.

Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение является уравнением эллиптического типа в точках ; параболического типа в точках ; и гиперболического типа в точках .

II. Чтобы привести уравнение к канонического виду, необходимо:

1. Определить коэффициенты ;

2. Вычислить выражение ;

3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );

4. Записать уравнение характеристик:

; (2)

5. Решить уравнение (2). Для этого:

а) разрешить уравнение (2) как квадратное уравнение относительно dy:

; (3)

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):

· (4)

в случае уравнения гиперболического типа;

· , (5)

в случае уравнения параболического типа;

· , (6)

в случае уравнения эллиптического типа.

6. Ввести новые (характеристические) переменные и :

· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т. е.

· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т. е. , в качестве берут произвольную, дважды дифференцируемую функцию , не выражающуюся через , т. е. ;

· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:

, (7)

8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:

· в случае уравнения гиперболического типа:

;

· в случае уравнения параболического типа:

;

· в случае уравнения эллиптического типа:

1.2. Пример выполнения задачи 1.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение гиперболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (9)

5. Решим уравнение (9). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy: ;

;

(10)

б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):

6. Введём характеристические переменные:

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на -100 (коэффициент при ):

Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид

где

1.3. Пример выполнения задачи 2.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты . В нашем примере они постоянны:

2. Вычислим выражение :

3. уравнение параболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (12)

5. Решим уравнение (12). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:

;

(13)

б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):

6. Введём характеристические переменные: одну из переменных вводим как и ранее

а в качестве берут произвольную, дважды дифференцируемую функцию, не выражающуюся через , пусть

;

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.

После деления на 25 (коэффициент при ):

Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид

где

1.4. Пример выполнения задачи 3.

Определить тип уравнения

(14)

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение эллиптического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (15)

5. Решим уравнение (15). Для этого:

а) разрешаем уравнение (15) как квадратное уравнение относительно dy: ; (16)

б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

(17)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на 4 (коэффициент при и ):

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид

где

1.5. Задачи для самостоятельного решения.

Определить тип уравнения и привести его к каноническому виду.

§2. Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2. 1. Необходимый теоретический материал

В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

(1)

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов

· в случае уравнения гиперболического типа:

; (11)

· в случае уравнения параболического типа:

; (12)

· в случае уравнения эллиптического типа:

. (13)

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

, (14)

где — новая неизвестная функция, — параметры, подлежащие определению. Такая замена не «испортит» канонического вида, но при этом позволит подобрать параметры так, чтобы из трех слагаемых группы младших производных в уравнении осталось только одно. Уравнения гиперболического, параболического и эллиптического типов соответственно примут вид

;

Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

(15)

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).

Здесь слева расставлены соответствующие коэффициенты уравнения (11). Собирая подобные слагаемые, получим

. (16)

В уравнении (16) приравняем к нулю коэффициенты при и

Откуда Подставив эти значения параметров в уравнение (16) и разделив его на , придем к уравнению

где .

2.2. Пример выполнения задачи 4

к каноническому виду и упростить группу младших производных.

9. Определим коэффициенты :

10. Вычислим выражение :

11. уравнение эллиптического типа во всей плоскости XOY.

12. Запишем уравнение характеристик:

. (18)

5. Решим уравнение (18). Для этого:

а) разрешаем уравнение (18) как квадратное уравнение относительно dy: ;

; (19)

б) найдём общие интегралы уравнений (19) (характеристики уравнения (17)):

6. Введём характеристические переменные:

13. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (17) при соответствующих производных.

14. Собирая подобные слагаемые, получим:

(20)

Теперь с помощью замены неизвестной функции (14)

упростим группу младших производных.

Пересчитаем производные, входящие в уравнение (20), используя формулы (15).

Здесь слева расставлены соответствующие коэффициенты уравнения (20). Собирая подобные слагаемые, получим

. (21)

В уравнении (21) приравняем к нулю коэффициенты при и

Откуда Подставив эти значения параметров в уравнение (21) и разделив его на , придем к уравнению

Ответ. Уравнение (20) является уравнением эллиптического типа на всей плоскости XOY. Его канонический вид

где .

2.3. Задачи для самостоятельного решения

Задача 4. Привести уравнения к каноническому виду и упростить группу младших производных.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ

О лабораторной работе № 2

на тему:

«Определение параметров нестационарного нелинейного уравнения регрессии»

2 курса 221 группы

Содержание

2.ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ………………………………………………………………………………………7 3.ПРОВЕРКА НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ МЕЖДУ ФАКТОРАМИ МОДЕЛИ……………………………………………………………………………………………8

4.ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ………………………………………………………………………11

5.ПРОВЕРКА СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ ………. 13

5.1.Проверка случайности колебаний уровней статочной последовательности………. 13

5.2. Проверка соответствия распределения случайной компоненты нормальному закону распределения……………………………………………………………………………………15

5.3.Проверка равенства математического ожидания случайной компоненты нулю………..16

5.4.Проверка независимости значений уровней случайной компоненты……………………17

5.5.Определение точности модели………………………………………………………………18

5.6. Тест ранговой корреляции Спирмена ……………………………………………………….19

6. ПРОВЕРКА НАЛИЧИЯ АНОМАЛЬНЫХ КОЛЕБАНИЙ ИССЛЕДУЕМОЙ МОДЕЛИ..21

7.ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ВИДА ЛИНИИ ТРЕНДА. ПРОГНОЗ ПОКАЗАТЕЛЕЙ…………………………………………………………………………………..22

Список использованной литературы………………………………………………25

ВВЕДЕНИЕ

Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. Центральной проблемой эконометрики является построение эконометрической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.

Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики — на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент временного ряда, на статистическом основании.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Задачей данной работы является оценка адекватности и точности нелинейной нестационарной модели уравнения регрессии с использованием персональных компьютеров.

Данная работа состоит из семи глав и трех приложении. Первая глава – постановка задачи.

Во второй главе осуществляется приведение исходного нелинейного уравнения регрессии к линейному по средствам замены переменных.

В третьей главе проверяется наличие мультиколлинеарности между факторами модели.

В главе 4 определяются параметры уравнения регрессии и строится искомое уравнение регрессии.

В пятой главе проверяется статистическая значимость уравнения регрессии. В пункте 5.1. осуществляется проверка колебаний уровней остаточной последовательности при помощи критерия серий, основанного на медиане выборки. В пункте 5.2. проводится проверка соответствия распределения случайной компоненты нормальному закону распределения при помощи показателей ассиметрии и эксцесса. В пункте 5.3. показана проверка равенства математического ожидания случайной компоненты нулю с использованием t-критерия Стьюдента. В пункте 5.4. проверяется независимость значений уровней случайной компоненты с целью выявления существующей автокорреляции остаточной последовательности. В данной работе эта проверка производится при помощи d-критерия Дарбина — Уотсона. В пункте 5.5. определяется точность модели. В качестве статистических показателей точности в данной работе используются следующие: среднеквадратичное отклонение, средняя относительная ошибка аппроксимации, коэффициент сходимости, коэффициент детерминации. В пункте 5.6 проверяется наличие или отсутствие гетероскедастичности исследуемой модели при помощи теста ранговой корреляции Спирмена.

В шестой главе осуществляется проверка на наличие аномальных колебании исследуемой модели с помощью метода Ирвина.

В восьмой главе определяется оптимальный вид линии тренда, которые отражены в приложениях, и прогнозируются показатели.

ПОСТАНОВКА ЗАДАЧИ

В данной работе необходимо рассмотреть нелинейную нестационарную модель изучаемого экономического объекта. В качестве объекта исследования представлен экономический процесс, о котором известны следующие статистические данные:

1. Y(t) — ставка % рефинансирования Центробанка;

2. X₁(t) — уровень безработицы, %

3. X₂(t) — уровень инфляции, %

Требуется найти коэффициенты нелинейной нестационарной модели уравнения множественной регрессии вида:

Y(t) — ставка % рефинансирования Центробанка;

X₁(t) — уровень безработицы, %

X₂(t) — уровень инфляции, %

Значения величин Y(t), X₁(t), Х₂(t) даны в Таблице №1 «Исходные данные». Данное нелинейное уравнение требуется привести к линейному уравнению вида:

(2)

Ø определить параметры уравнения регрессии, используя замену переменной;

Ø проверить наличие мультиколлинеарности между факторами;

Ø проверить статистическую значимость уравнения в целом и отдельных коэффициентов уравнения. Это позволит оценить адекватность полученной модели исследуемому процессу и возможность её использования для осуществления анализа и проектирования;

Ø проверить отсутствие гетероскедастичности и автокорреляции остатков исследуемой модели, установить адекватность и точность уравнения регрессии;

Ø проверить наличие аномальных наблюдений, используя метод Ирвина.

Таблица №1

ИСХОДНЫЕ ДАННЫЕ

T	X₁	X₂	Y
25,22
21,52
22,32
21,77
20,66
20,14
17,66
17,08
16,87
18,63
16,51
16,95
19,38
18,14
17,94
19,69
19,38
15,88
16,58
14,64

ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ

Многие экономические процессы наилучшим образом описываются нелинейными уравнениями регрессии. Например, функции спроса и производственные функции. И в этом случае мы не можем применить к ним обычный метод наименьших квадратов и использовать стандартные подходы к оценке статистической надежности.

В связи с этим встает задача о возможности привести нелинейное уравнение к линейному виду.

В тех случаях, когда нелинейность касается факториальных переменных, но не связано с коэффициентами уравнения регрессии, нелинейность обычно устраняется путем замены переменной.

Рассмотрим нелинейное нестационарное уравнение: