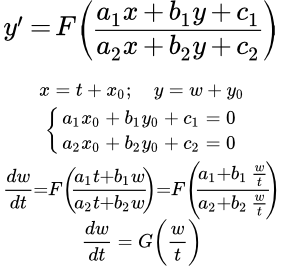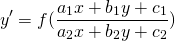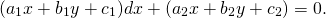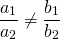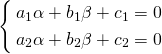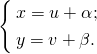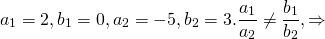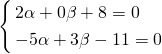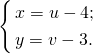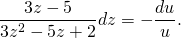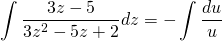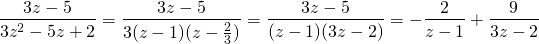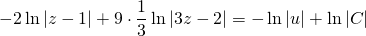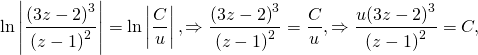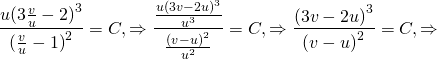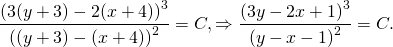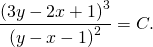Приведение к однородному заменой дифференциальные уравнения

К однородным уравнениям первого порядка приводится уравнение вида:
(1) ,
где f – функция.

Видео:6. Дифференциальные уравнения, приводящиеся к однороднымСкачать

Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
a ₁ x + b ₁ y + c ₁ , a ₂ x + b ₂ y + c ₂ ,
и выполнить замену:
a ₁ x + b ₁ y + c ₁ → t ( a ₁ x + b ₁ y + c ₁ ) ;
a ₂ x + b ₂ y + c ₂ → t ( a ₂ x + b ₂ y + c ₂ ) .
Если, после преобразований, t сократится, то это уравнение приводится к однородному.

Пример

Определить, приводится ли данное дифференциальное уравнение к однородному:
.

Выделяем две линейные формы:
x + 2 y + 1 и x + 4 y + 3 .
Первую заменим на t ( x + 2 y + 1) , вторую – на t ( x + 4 y + 3) :
.
По свойству логарифма:

.
t сокращается:
.
Следовательно, это уравнение приводится к однородному.

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Решение дифференциального уравнения, приводящегося к однородному уравнению

Решаем систему уравнений:
(2)

Здесь возможны три случая.

1) Система (2) имеет бесконечное множество решений (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 совпадают). В этом случае
;
.
Тогда
.
Это простейший вид уравнения с разделяющимися переменными:
.
Его решение:
y = Ax + C .

2) Система (2) не имеет решений (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 параллельны). В этом случае a ₁ b ₂ = a ₂ b ₁ .
Применим это соотношение.

.

Это означает, что a ₂ x + b ₂ y + c ₂ является функцией от a ₁ x + b ₁ y + c ₁ . Поэтому является функцией от a ₁ x + b ₁ y + c ₁ . То есть f является функцией от a ₁ x + b ₁ y + c ₁ . Обозначим такую функциею как g . Тогда исходное уравнение (1) имеет вид:
.
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой
z = a ₁ x + b ₁ y + c ₁ .

3) Система (2) имеет одно решение (прямые a ₁ x + b ₁ y + c ₁ = 0 и a ₂ x + b ₂ y + c ₂ = 0 пересекаются в одной точке). Обозначим это решение как x ₀ , y ₀ . Тогда
(3)
Делаем подстановку x = t + x ₀ , y = u + y ₀ , где u – это функция от t . Тогда
dx = dt, dy = du ;

.
Или
.
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = z t , где z – это функция от t .

Видео:Однородное дифференциальное уравнениеСкачать

Пример решения дифференциального уравнения, приводящегося к однородному уравнению первого порядка

Решить уравнение
(П.1) .

1) Проверим, приводится ли это дифференциальное уравнение к однородному. Для этого выделяем две линейные формы:
2 x – y + 4 и x – 2 y + 5 .
Первую заменим на t (2 x – y + 4) , вторую – на t ( x – 2 y + 5) :
.
Делим на t :
.
t сократилось, поэтому это уравнение приводится к однородному.

2) Решаем систему

Из первого уравнения y = 2 x + 4 . Подставляем во второе:
x – 2(2 x + 4) + 5 = 0 ;
x – 4 x – 8 + 5 = 0 ;
– 3 x = 3 ;
x = – 1 ;
y = 2 x + 4 = 2·(–1) + 4 = 2 .
Итак, мы нашли решение системы:
x ₀ = –1 , y ₀ = 2 .

3) Делаем подстановку:
x = t + x ₀ = t – 1 ;
y = u + y ₀ = u + 2 ,
где u – функция от t . dx = dt, dy = du , ;
;
.
Подставляем в (П.1):
(П.2) .
Это – однородное уравнение.

4) Решаем однородное уравнение (П.2). Делаем подстановку:
u = z · t , где z – функция от t .
u′ = ( z · t ) ′ = z′t + z t′ = z′t + z .
Подставляем в (П.2):
.
Сокращаем на t и выполняем преобразования:
;
;
.
Разделяем переменные – умножаем на dt и делим на t ( z 2 – 1) . При z 2 ≠ 1 получаем:
.
Интегрируем:
(П.3) .
Вычисляем интегралы:
;

.
Подставляем в (П.3):
.
Умножим на 2 и потенцируем:
;
.
Заменим постоянную e 2 C → C . Раскроем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C . Умножим на ( z + 1) 2 и применим формулу: z 2 – 1 = ( z – 1)( z + 1) .
.
Сократим на ( z – 1) :
.
Возвращаемся к переменным u и t , используя формулу: u = z t . Для этого умножим на t :
;
;
.
Возвращаемся к переменным x и y , используя формулы: t = x + 1 , u = y – 2 .
;
(П.4) .

Теперь рассмотрим случай z 2 = 1 или z = ±1 .
;
.
Для верхнего знака «+» имеем:
;
.
Это решение входит в общий интеграл (П.4) при значении постоянной C = 0 .
Для нижнего знака «–»:
;
.
Эта зависимость также является решением исходного дифференциального уравнения, но не входит в общий интеграл (П.4). Поэтому к общему интегралу добавим решение
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 30-07-2012 Изменено: 22-06-2015

Видео:Дифференциальные уравнения 1-го порядка, приводящиеся к однородным (практика)Скачать

Однородные дифференциальные уравнения
и приводящиеся к ним

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Как решать дифференциальные уравнения, приводящиеся к однородным

Некоторые уравнения могут быть приведены к однородным. Дифференциальные уравнения, приводящиеся к однородным, имеют вид:

либо в другой форме записи

Рассмотрим три возможных случая.

Собственно, это и есть дифференциальные уравнения, приводящиеся к однородным, поскольку в двух других случаях переходим непосредственно к уравнениям с разделяющимися переменными. Такие уравнения решают с помощью замены переменных.

В этом случае решаем систему уравнений

Отсюда находим значения α и β и делаем замену

Откуда dx=du, dy=dv, y’=dv/du. Эта замена позволяет нам получить однородное дифференциальное уравнение 1-го порядка.

решаем систему уравнений

Откуда α=-4, β=-3. Замена

dx=du, dy=dv. Подставляем и упрощаем:

2udu+(3v-5u)dv=0. Это однородное дифференциальное уравнение 1-го порядка относительно переменных u и v. Выполняем замену z=v/u,откуда v=uz, dv=zdu+udz. Подставляем:

(2udu+3uz²du-5uzdu)+(3u²zdz-5u²dz)=0. Делим обе части на u≠0:

(2+3z²-5z)du+(3z-5)dz=0. Получили уравнение с разделяющимися переменными. Разделяем переменные: u(3z-5)dz=-(2+3z²-5z)du. Для этого делим обе части на u(2+3z²-5z)≠0, имеем:

В правой части — табличный интеграл. Рациональную дробь в левой части раскладываем на простые множители:

Применяем свойства логарифмов:

теперь — обратная замена

Геометрический смысл такой замены: начало координат переносится в точку пересечения прямых

и в новой системе свободные члены в уравнениях прямых равны нулю.

Перейдем к рассмотрению двух других случаев решения дифференциальных уравнений такого вида.

📽️ Видео

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

10. Уравнения БернуллиСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать