Предположим, что известен электромагнитный процесс, описываемый следующими уравнениями Максвелла:
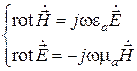
Обращает на себя внимание симметрия этих двух уравнений. Действительно, уравнения переходят одно в другое при замене вида
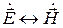
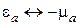
Последние соотношения являются математическим выражением принципа перестановочной двойственности для электромагнитного поля, обоснованного впервые А. А. Пистолькорсом в 1944 г.
Физическое содержание этого принципа заключается в следующем. Если известно полное решение какой-либо электромагнитной задачи, то простая перестановка позволяет автоматически получить решение двойственной (дуальной) задачи, в которой конфигурация линий электрического поля повторяет аналогичную конфигурацию линий магнитного поля в исходном электромагнитном процессе и наоборот. При этом, поскольку в результате перестановки уравнения Максвелла не меняют своего вида, двойственный электромагнитный процесс действительно существует.
Естественно считать, что исходное электромагнитное поле возбуждается сторонними электрическими токами. В этом случае можно полагать, что двойственный процесс возбуждается сторонними магнитными токами, как это было показано в предыдущем разделе. Однако для сохранения симметрии уравнений Максвелла плотность стороннего магнитного тока должна быть введена во второе уравнение с обратным знаком. Таким образом, получаем систему уравнений Максвелла с учетом сторонних магнитных токов:
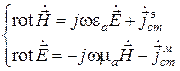
Дополнительное перестановочное соотношение для плотностей сторонник токов приобретает вид
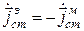
- Магнитные токи. Магнитные заряды (определение, назначение). Уравнения Максвелла с учетом магнитных токов и зарядов. Принцип перестановочной двойственности
- Лабораторная работа № ВИ-104 Элементарные излучатели
- Поле в ближней зоне
- Поле в дальней зоне
- Элементарный магнитный излучатель
- Элемент Гюйгенса
- 📹 Видео
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Магнитные токи. Магнитные заряды (определение, назначение). Уравнения Максвелла с учетом магнитных токов и зарядов. Принцип перестановочной двойственности
Магнитный ток— это два течения, одно течение сформировано единичными магнитами северного полюса другое магнитами южного полюса , и они создают один встречно-текущий закрученный подобно винту поток, обладающий высокой скоростью. Одно течение, если это будет течение магнитов северного полюса или течение магнита южного полюса, не может существовать отдельно. Чтобы сформировать поток, одно течение должно двигаться встречно другому.
Существуют магнитные заряды — монополи – квазичастицы, несущие на себе только положительный или только отрицательный магнитный заряд. Они не связаны в пары и могут передвигаться по отдельности. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля. Магнитный монополь — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у всех известных магнитов всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Все известные элементарные частицы, обладающие электромагнитным полем, являются магнитными диполями.
Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими 
Принцип перестановочной двойственности- инвариантность однородной системы Максвелла уравнений относительно замены 















Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Лабораторная работа № ВИ-104 Элементарные излучатели
К КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА
Институт радиоэлектроники и телекоммуникаций
Лаборатория «Электродинамика и распространение радиоволн»
Лабораторная работа № ВИ-104
Целью работы является изучение элементарных излучателей электромагнитного поля и исследование их свойств с помощью виртуальной лабораторной установки.
2. Подготовка к работе.
Перед выполнением работы необходимо изучить соответствующий лекционный материал, настоящее описание и, при необходимости, рекомендованную литературу [1, с.206-220; 2, с.126-136; 3, с.163-181; 4, с.106-129; 5, с.137-166].
3. Краткие теоретические сведения.
Устройство, предназначенное для излучения электромагнитных волн, называют излучателем или передающей антенной. Любую антенну можно представить в виде совокупности простейших элементарных излучателей. Различают элементарный электрический излучатель, элементарный магнитный излучатель и элемент Гюйгенса – элементарный поверхностный излучатель.
Элементарный электрический излучатель
Элементарным электрическим излучателем называют элемент электрического линейного гармонического тока, для которого известно, что: во-первых, его длина 

Пусть ось 




Поскольку этот ток изменяет свое значение только в точках: 



и, следовательно, равные друг другу по величине и противоположные по знаку:


причем
Элементарный электрический излучатель со строго неизменным вдоль его длины 
Пусть в однородной среде без потерь с параметрами 


Комплексные амплитуды векторов поля этого излучателя определим через векторный потенциал.
Если поместить начало координат O в центре элементарного излучателя (рис.1) и обозначить расстояние r между точкой наблюдения 




Рис.1. Элементарный электрический излучатель
Из (4) следует, что векторный потенциал элементарного электрического излучателя направлен в точке наблюдения параллельно его оси и зависит только от расстояния R, представляющего собой радиальную координату точки наблюдения в сферической системе координат, начало которой совмещено с центром излучателя. Поэтому дальнейшие преобразования целесообразно проводить в сферической системе, направление полярной оси которой совпадает с током излучателя (рис.2).
В точке наблюдения M орт-вектор разложим в сферической системе координат по двум взаимно перпендикулярным направлениям ( рис. 2):

Рис.2. Сферическая система координат
Тогда векторный электрический потенциал 



Векторный электрический потенциал определяет напряжённость магнитного поля




Для определения напряжённости электрического поля воспользуемся первым уравнением Максвелла:




Электромагнитное поле (8), (10) – (12) не зависит от азимутального угла 

Поле в ближней зоне
Ближняя зона, или зона индукции, характеризуется такими расстояниями R точки наблюдения от излучателя, для которых 







Учитывая, что 



В ближней зоне векторы поля в точке наблюдения в момент времени t определяются значениями тока в этот же момент времени. Таким образом, ближняя зона представляет собой область квазистационарного поля. Использованное нами приближенное соотношение 
Вектор Пойнтинга в ближней зоне имеет две составляющие:


Компоненты напряженности электрического поля (14), (15) отстают по фазе от напряженности магнитного поля (16) на 





Поле в дальней зоне
Дальняя зона характеризуется такими расстояниями R точки наблюдения от излучателя, для которых 



где 
Перейдя к мгновенным значениям, имеем:


Согласно (20), (21) в среде без потерь векторы 




Подставив в (22) два последовательных момента времени 




Вектор 

Рис.3. Вектора поля излучения элементарного электрического излучателя
При этом мгновенные значения векторов связаны между собой соотношениями:


Вектор Пойнтинга в дальней зоне имеет только одну радиальную составляющую:

Причем ее мгновенное значение всегда оказывается положительным вследствие того, что векторы поля имеют одинаковую фазу колебаний. Это означает, что энергия движется в направлении радиусов только от излучателя. Она не возвращается обратно к излучателю и представляет собой энергию излученной электромагнитной волны.
Это поле называют полем излучения, а дальнюю зону называют также зоной излучения или волновой зоной.
Рассмотрим зависимость амплитуд векторов поля излучения от сферических координат 

Входящая в выражения для амплитуд векторов поля излучения антенны функция угловых сферических координат 
Согласно (20), (21) характеристика направленности элементарного электрического излучателя 




Рис.4. Характеристика направленности элементарного электрического излучателя
Элементарный магнитный излучатель
Если в некотором объеме 


В этом случае первичное возбуждение электромагнитного поля вызывается известной в каждой точке объема 

которую по аналогии с плотностью стороннего электрического тока 
Напомним, что в природе не существует магнитных зарядов и магнитного тока, представляющего собой упорядоченное движение этих зарядов. Поэтому формулу (26) следует рассматривать как результат формального введения в теорию фиктивных магнитных зарядов и обусловленных ими фиктивных магнитных токов, благодаря которому приобретается удобство в описании магнитных полей.
Если монохроматическое поле обусловлено электрическими токами и фиктивными магнитными токами, то оно удовлетворяет симметричным уравнениям Максвелла следующего вида:


Из симметрии соотношений (27), (28) следует, что при известном решении задачи при заданных сторонних электрических токах 




Конечно, это возможно только в том случае, если в обеих задачах одинакова форма поверхности 
Этот прием называют принципом перестановочной двойственности уравнений Максвелла. Этот принцип широко используется при решении различных задач и имеет большое практическое значение.
Элементарным магнитным излучателем называют элемент фиктивного магнитного линейного гармонического тока, для которого известно, что: во-первых, его длина 

Поле, которое создает элементарный магнитный излучатель в безграничной однородной среде без потерь, проще всего найти с помощью принципа перестановочной двойственности, позволяющего сразу перейти от известного нам поля элементарного электрического излуча, (21) к искомому полю:


По своей структуре формулы (30), (31) аналогичны (20), (21). Поэтому отмеченные выше особенности поля излучения электрического излучателя полностью присущи и полю излучения элементарного магнитного излучателя. Поверхностью равных фаз является сфера, вектора поля лежат по касательной к ней, они взаимно ортогональны и пропорциональны по величине, сохраняется форма диаграммы направленности. Различие между полями электрического и магнитного элементарных излучателей состоит в разной ориентировке в пространстве векторов (рис.5.42).
Рис.5. Вектора поля излучения элементарного магнитного излучателя
Простейшей физически осуществимой моделью элементарного магнитного излучателя является плоская проводящая рамка (одиночный виток провода) с электрическим током, периметр которой весьма мал по сравнению с длиной волны 


Элемент Гюйгенса
Элементом Гюйгенса называют элемент 



Совместим начало декартовой системы координат 







Рис.6. Элемент Гюйгенса
При определении поля элемента Гюйгенса в полупространстве 







Элемент электрического тока 



Определим поле элемента Гюйгенса в дальней зоне, т. е. на расстояниях 



В дальней зоне электромагнитному полю элемента Гюйгенса присущи все основные особенности поля излучения элементарных излучателей. Это поле представляет собой сферические бегущие волны, расходящиеся в полупространстве 



Определим амплитуду поля элемента Гюйгенса:

Следовательно, амплитудная характеристика направленности, определяющая зависимость амплитуды поля от угловых координат, одинакова во всех меридиональных полуплоскостях и выражается формулой:

Выражение (36) является уравнением кардиоиды (рис.7).
Рис.7. Диаграмма направленности элемента Гюйгенса
Пространственная характеристика направленности представляет собой тело вращения кардиоиды рис.7 вокруг оси 
4. Описание лабораторной установки.
С помощью виртуальной лабораторной установки планируется изучать изменение продольной и поперечной компонент напряженности электрического поля от расстояния до элементарного электрического излучателя. Кроме того, должна иметься возможность наблюдать диаграммы направленности элементарных излучателей и определять их характеристики.
В верхней части лицевой панели лабораторной установки расположен заголовок «Исследование элементарных излучателей» и кнопка останова STOP (рис.8).
Виртуальная лабораторная установка состоит из двух частей, отображаемых в двух страницах на экране: «Компоненты поля элементарного электрического излучателя»(рис.8) и «Диаграммы направленности элементарных излучателей» (рис.9).
Рис.8. Лицевая панель ВИ «Элементарные излучатели». Страница «Компоненты поля элементарного электрического излучателя»
Работа с установкой начинается в закладке «Компоненты поля элементарного электрического излучателя». Справа на ней находится графический индикатор «Амплитуда компоненты поля», на котором отображаются зависимости продольной и поперечной составляющих поля от расстояния между излучателем и точкой наблюдения.
Под индикатором находится панель управления двумя курсорами, в которой имеются названия измеряемых компонент поля «Продольная компонента» и «Поперечная компонента» и окна с координатами курсоров.
В левой верхней части расположен регулятор, задающий значение угловой координаты «Угол от оси излучателя».
Ниже расположен регулятор размера шкалы расстояния (горизонтальная шкала экрана).
На странице «Диаграммы направленности элементарных излучателей» находится два графических индикатора. На левом индикаторе диаграмма направленности отображается в декартовой системе координат. Под индикатором есть панель управления курсором, позволяющая измерять графики на экране.
Рис.9. Лицевая панель ВИ «Элементарные излучатели». Страница «Диаграммы направленности элементарных излучателей»
На правом индикаторе диаграмма направленности отображается в полярных координатах.
Над экранами имеется переключатель на три положения: «Электрический», «Магнитный», «Площадка». Он осуществляет переключение на экране всех изучаемых элементарных излучателей.
Включение прибора осуществляется нажатием на двунаправленную стрелку в строке кнопок окна LabVIEW, расположенная правее заголовка кнопка STOP выключает виртуальную лабораторную установку.
5. Порядок выполнения работы.
1. Запустить лабораторную установку «Элементарные излучатели», ознакомиться с органами управления.
2. Перейти на страницу «Компоненты поля элементарного электрического излучателя». Выполнить исследования в соответствии с вариантом, выбранным в таблице 1.
Таблица 1. Исходные параметры для исследования элементарных излучателей радиоволн
📹 Видео
Билеты №32, 33 "Уравнения Максвелла"Скачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

3 14 Уравнения МаксвеллаСкачать

Маятник Максвелла.Скачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Основные физические понятия технической электродинамики, 1978Скачать
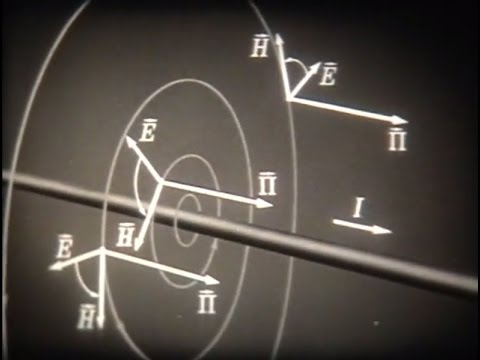
Физические ошибки. Уравнения МаксвеллаСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Теория поля 6. Вторая пара уравнений Максвелла. Законы сохранения ЭМ поля.Скачать

3 Уравнения Максвелла в дифференциальной формеСкачать

Раскрытие тайн электромагнитной волныСкачать

6.5 Поле элементарного магнитного излучателя. Физические модели магнитного излучателяСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
Лекция №18 "Модуляция (часть 2). Уравнения Максвелла"Скачать

Урок 155. Изучение распределения МаксвеллаСкачать

Двойственные функции ПрактикаСкачать












