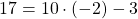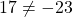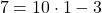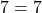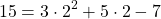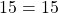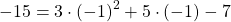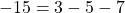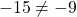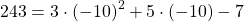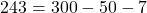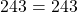Принадлежит ли точка графику уравнения (6 видео)

Принадлежит ли графику функции точка

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.

Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.

Ответ: точки A и C принадлежат графику функции.

Содержание

График линейной функции, его свойства и формулы
Понятие функции
Понятие линейной функции
Свойства линейной функции
Построение линейной функции
Решение задач на линейную функцию
Принадлежность точки отрезку. Почему не работает классика?
Причины и постановка задачи
Классическое уравнение
Расширенная классика
Модификация уравнения
Итоговая функция
Почему такая большая функция получилась?
Классика всегда в моде или Математика — царица наук
Скачать
🎬 Видео

Видео:8 класс. График функции. Принадлежит ли точка графику функции. Как узнать?Скачать

График линейной функции, его свойства и формулы

О чем эта статья:

Видео:7 кл.Принадлежит ли графику функции 3x+4y=12 точка А(4;1)Скачать

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Видео:Определить, принадлежит ли точка с заданными координатами графику функцииСкачать

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

х	0	2	4
y	-2	-1	0

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Видео:Принадлежит ли точка графику функции. Алгебра 7 классСкачать

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

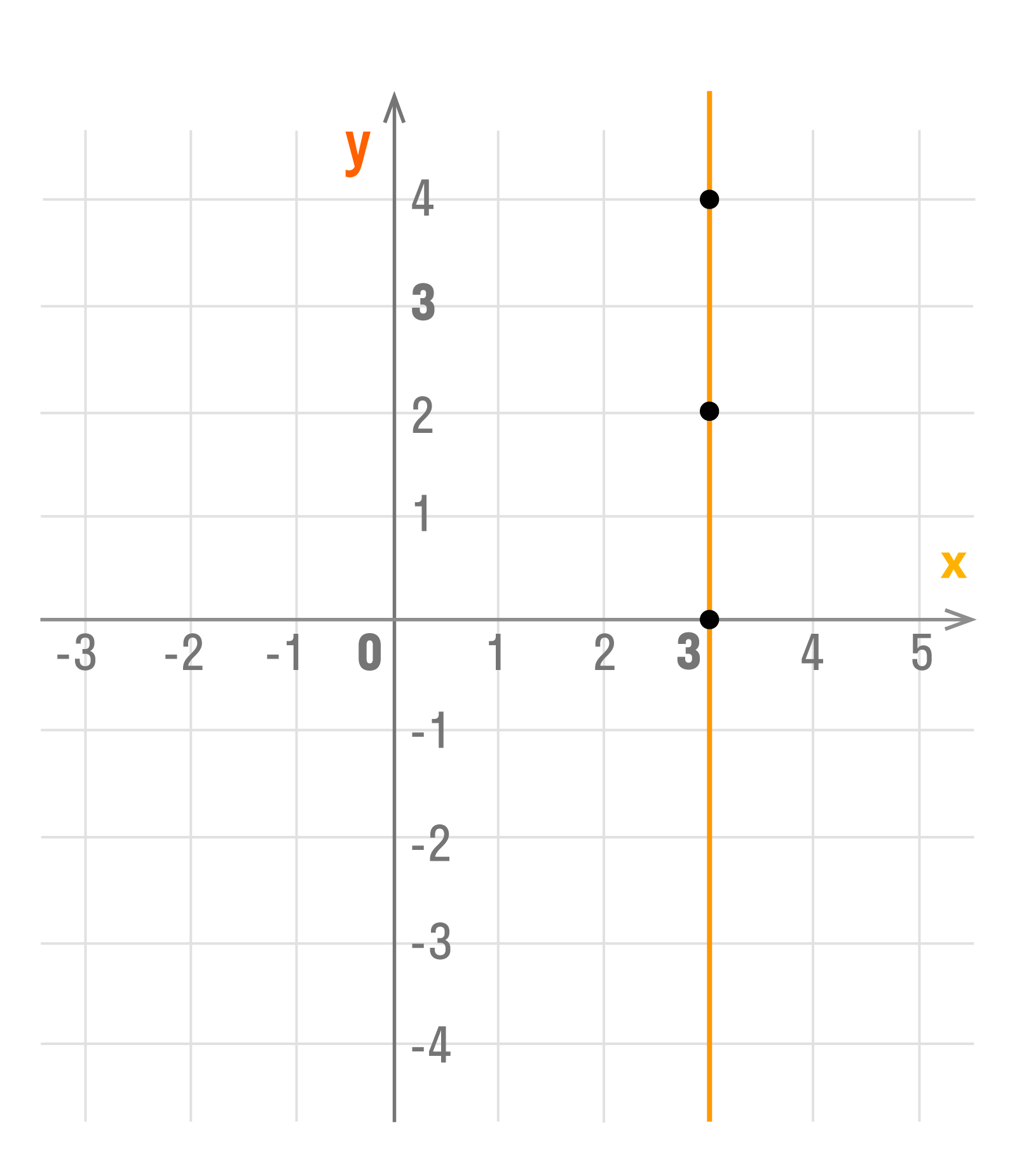
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Видео:Как проверить, принадлежит ли точка с заданными координатами графику данной функцииСкачать

Принадлежность точки отрезку. Почему не работает классика?

IP76 > Векторная графика > Принадлежность точки отрезку. Почему не работает классика?

Определить принадлежность точки отрезку, казалось бы, вполне себе тривиальная задача из школьного курса геометрии. Однако, есть определенные нюансы, которые заставляют усомниться в верности классической формулы:

Видео:Как построить график линейной функции.Скачать

Причины и постановка задачи

Запросы «как найти принадлежность точки отрезку» уводят на страницу «Пересечение прямых, угол и координаты пересечения», где есть пункт «Принадлежность точки отрезку». В нем рассматривается факт принадлежности точки отрезку, уже после того, как мы определили точку пересечения прямых. То есть точка уже принадлежит прямым, и это абсолютно точно. Осталось только определиться, точка в отрезке между двумя точками отрезка, либо где-то на прямой мимо них.

Людям свойственно искать готовые решения, и код, представленный в статье вряд ли удовлетворит запросу «как найти принадлежность точки отрезку, заданный двумя точками«. Поэтому здесь задачу так и сформулируем:

Есть отрезок, заданный точками P1(x1,y1) и P2 (x2,y2) . Необходимо определить, принадлежит ли точка P(x,y) этому отрезку.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Классическое уравнение

Предположим, вы делаете векторный редактор. Необходимо по курсору мыши определить попадает ли точка в ранее нарисованный отрезок. В этом многотрудном деле такая задача возникает всегда.

Для совместимости с Delphi 7 введем тип вещественной точки:

Почему бы не сделать сразу TPointF вместо типа TxPoint? Просто у меня гора старых исходников, где используется этот тип, а никакого TPointF не было ни в помине, ни в планах. Delphi 7 казалась вершиной инженерной мысли на тот момент.

В предложение uses дописываем следующее (ради TPointF, и чтобы компилятор XE не доставал хинтами):

Почему именно XE5? Если честно, нет возможности проверить, не ставить же ради этого всю линейку дельфей. Но в XE5 вещественная точка точно есть, а в Delphi 7 ее точно нет. Вот этим и объясняется выбор версии компилятора в директиве. Одни говорят, что TPointF появился в XE2, другие — аж в Delphi 2010. Короче, с таким директивным условием будет работать везде и точка.

Пишем небольшую функцию, которая использует классическое уравнение прямой, проходящей через две различные точки на плоскости, представленное выше.

SameValue — сравнивает два вещественных числа с учетом погрешности Epsilon. Находится в модуле Math, который надо подключить в предложении uses секции implementation.

Что происходит. Вначале проверяется допустимость координаты точки внутри координат отрезка. Условие необходимое, но недостаточное. Если координата может принадлежать отрезку, третьим условием проверяем нахождение точки на прямой, проходящей через точки отрезка.

Рис.1. Курсор точно на линии, но не определяет, что точка принадлежит отрезку

Если мы попытаемся по координатам курсора мыши определить, попала ли точка в отрезок, нас ждет фиаско. Складывается ощущение, что формула не работает, алгебра — отстой, все в жизни не так.

Видео:Определим,проходит ли график через данную точку.Скачать

Расширенная классика

Для начала навесим на функцию еще пару условий, чтобы определить попадание в точки, задающие отрезок.

Ну, во-первых, вот и разгадка, куда делись значения 1 и 2 из результатов предыдущей функции. Во-вторых, теперь в конечные точки отрезка попадает отлично, но между ними по-прежнему не хочет работать.

На самом деле — математика по-прежнему царица наук, а мы пытаемся повенчать розу белую с черной жабой.

Выведем в интерфейс значения dx = (p2.x-p1.x), dy = (p2.y-p1.y) и т.д. Плюс результат работы функции (p.x-p1.x)*(p2.y-p1.y) — (p.y-p1.y)*(p2.x-p1.x). И убедимся, что при самых казалось бы максимально возможных приближениях к отрезку, результат ошеломляет своей двух- или трехзначной непохожестью на ноль.

Рис.2. Теперь определяет конечные точки, но между ними по-прежнему работает так себе…

Конечно, используя операцию умножения вместо деления, мы избегаем деления на ноль, укорачиваем код. Но при этом надо помнить, что умножение даже 1 на 12, это уже далеко от нуля, а если появляется еще и минус в разницах, то от нуля мы улетаем очень быстро и очень ощутимо.

На рисунке 2 прицел точно на линии, но разность координат, которую получаем из классического уравнения, и которая должна быть равна нулю, между тем равна:

Функция применима в точных расчетах, но не в векторном редакторе.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Модификация уравнения

Очевидно, надо вычислять как-то иначе. Например вычислять Y по имеющейся координате X и сравнивать с имеющейся координатой Y. Если разница меньше заданного Epsilon — точка принадлежит отрезку. Выразим Y из используемого уравнения прямой. Итак, дано:

Выразим Y:

И напишем еще одну функцию, в которой учтем ситуацию, когда (X₂-X₁) может быть равно нулю. Это ситуация вертикальной (или почти вертикальной) прямой.

Epsilon уже выступает, и как точность вычислений, и как допуск, при котором мы считаем, что точка на отрезке. Невозможно скрупулезно попасть мышкой в нужную точку отрезка, которая сама по себе уже есть огромное приближение к действительности. Все мы помним и любим Брезенхэма.

Рис.3. Все здорово определяет с учетом погрешности Epsilon=12 pix

Но, даже если мы упростили себе процесс «попадания» в отрезок, мы должны знать точные координаты на отрезке. Для этого у нас и появился тип вещественной точки TxPoint и возвращаемый параметр res. В этой версии функции мы производим расчет реальной точки на отрезке.

На рисунке 3 расчетная точка и ее координаты выделена коричневым цветом.

Однако, все равно есть нюанс. Если линия сильно вертикальна, то есть расстояние (X₂-X₁) невелико, попадать в линию все равно трудно.

Рис.3.1. На почти вертикальной линии функция снова капризничает

Связано с тем, что при уменьшении делителя, коим разность по X выступает в нашем случае, сильно вырастает результат, и чем расстояние (X₂-X₁) меньше, тем труднее попасть в Epsilon.

Видео:Вариант 72, № 2. Выбрать точку, принадлежащую графику уравнения ax+by=cСкачать

Итоговая функция

В стремлении к совершенству, всегда что-то незамысловатое, в пару строк кода, разрастается в какую-то все учитывающую портянку листинга.

Давайте проверять, что больше (X₂-X₁) или (Y₂-Y₁), и в зависимости от результата, будем высчитывать либо Y, либо X. Формулу для X не привожу, он очевидна.

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Почему такая большая функция получилась?

В функции помимо факта принадлежности точки отрезку, также осуществляется проверка на конечные точки — чтобы можно было менять их расположение мышкой. Также, функция возвращает «истинную» точку на отрезке, полученную из приближенной, содержащую погрешность Epsilon.

Можно сократить, не считать конечные точки, не анализировать «вертикальность» и «горизонтальность». Можно взять за настоящую ту точку, которую анализируем и не считать «истинную». Код в этом случае сильно сократиться. Поэтому лучше иметь полный комплект, из которого можно удалить «лишнее» на ваш взгляд.

Зачем нужны такие ощутимо большие проверки на вертикальность и горизонтальность. Ну, во-первых мы освобождаем от условий последний блок вычислений, во-вторых, если убрать, скажем, проверку на dy, погрешность станет в два раза меньше. Потому что отработает это условие: Abs(p1.Y-p.Y) + Abs(p2.Y-p.Y). Имея идеальную горизонтальную линию, подведя курсор на Epsilon допустимый интервал, мы получим в итоге Epsilon + Epsilon = 2 * Epsilon и условие конечно не сработает. Сработает, если подведем на расстояние в два раза меньшее Epsilon.

Если всех этих тонкостей не требуется, можно смело использовать либо эту, либо вообще эту функцию.

Видео:Как построить график функции без таблицыСкачать

Классика всегда в моде или Математика — царица наук

Теперь давайте полученную в результате предыдущей функции вещественную точку res подставим в первую функцию. И убедимся, что теоретическая принадлежность точки отрезку работает прекрасно, просто в пространстве грубых целочисленных точек мы не в состоянии гарантированно получить такую точку, которая удовлетворила бы уравнению. Но если мы ее рассчитаем и получим значения с плавающей запятой — все заработает как надо.

Рис.5. Результат применения рассчитанной точки для первой функции

На рисунке 5 добавлен результат функции f(x,y)=(x-x₁) * (y₂-y₁) — (y-y₁) * (x₂-x₁) для рассчитанной точки на отрезке. Он равен, как и следовало ожидать, нулю. А также результат вызова первой функции, которая использует это уравнение и возвращает 3, если точка принадлежит отрезку. Что мы воочию и видим.

1)Поэтому в графике надо избегать типов TPoint, даже если это вызывает необходимость постоянно их округлять для функций GDI.

2)Поэтому функция правильная, классическая формула работает, просто в пространстве компьютерных упрощений надо использовать ту же самую формулу, но в другом качестве.

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Скачать

Друзья, спасибо за внимание!

Надеюсь, материал был полезен.

Не пропустите новых интересных штуковин, подписывайтесь на телегу. )))

Если есть вопросы, с удовольствием отвечу.

Исходники и исполняемый файл для GDI и Delphi 7. Проверен в XE 7, XE 10.

Исходники (Delphi 7, XE7, XE10) 11 Кб

Исполняемый файл (zip) 213 Кб

Как подключить GDI+ в Delphi 7 и без проблем скомпилировать в XE 7, XE 10 читаем в этой статье. Там же забираем исходники.

Чтобы нарисовать отрезок, нажмите мышь и, не отпуская, ведите курсор. При отпускании отрезок зафиксируется. При повторном нажатии начнет рисоваться новый отрезок.

За концы отрезка можно таскать. Если попали на отрезок, т.е. видна коричневая точка, можно таскать весь отрезок.