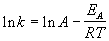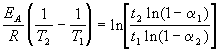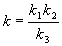Примеры задач на уравнение аррениуса

Из качественных соображений понятно, что скорость реакций должна увеличиваться с ростом температуры, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения — правило Вант-Гоффа и уравнение Аррениуса.

Правило Вант-Гоффа заключается в том, что при нагревании на 10 о С скорость большинства химических реакций увеличивается в 2 4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом:

, (4.1)

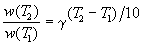
где — температурный коэффициент скорости ( = 24). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.

Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости:

, (4.2)

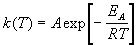
где R — универсальная газовая постоянная; A — предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом реакции; E_A — энергия активации, которую можно охарактеризовать как некоторую пороговую энергию: грубо говоря, если энергия сталкивающихся частиц меньше E_A, то при столкновении реакция не произойдет, если энергия превышает E_A, реакция произойдет. Энергия активации не зависит от температуры.

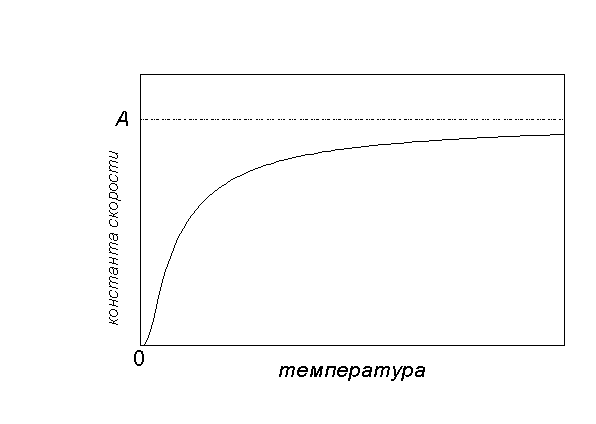
Графически зависимость k(T) выглядит следующим образом:

При низких температурах химические реакции почти не протекают: k(T) 0. При очень высоких температурах константа скорости стремится к предельному значению: k(T) A. Это соответствует тому, что все молекулы являются химически активными и каждое столкновение приводит к реакции.

Энергию активации можно определить, измерив константу скорости при двух температурах. Из уравнения (4.2) следует:

. (4.3)

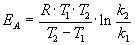
Более точно энергию активации определяют по значениям константы скорости при нескольких температурах. Для этого уравнение Аррениуса (4.2) записывают в логарифмической форме

и записывают экспериментальные данные в координатах ln k — 1/T. Тангенс угла наклона полученной прямой равен —E_A / R.

Для некоторых реакций предэкспоненциальный множитель слабо зависит от температуры. В этом случае определяют так называемую опытную энергию активации:

. (4.4)

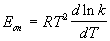
Если предэкспоненциальный множитель — постоянный, то опытная энергия активации равна аррениусовской энергии активации: E_оп = E_A.

Пример 4-1. Пользуясь уравнением Аррениуса, оцените, при каких температурах и энергиях активации справедливо правило Вант-Гоффа.

Решение. Представим правило Вант-Гоффа (4.1) как степенную зависимость константы скорости:

,

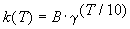
где B — постоянная величина. Сравним это выражение с уравнением Аррениуса (4.2), приняв для температурного коэффициента скорости значение

.

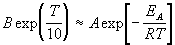
Возьмем натуральный логарифм обеих частей этого приближенного равенства:

.

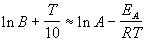
Продифференцировав полученное соотношение по температуре, найдем искомую связь связь между энергией активации и температурой:

.

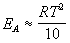
Если энергия активации и температура примерно удовлетворяют этому соотношению, то правилом Вант-Гоффа для оценки влияния температуры на скорость реакции пользоваться можно.

Пример 4-2. Реакция первого порядка при температуре 70 о С завершается на 40% за 60 мин. При какой температуре реакция завершится на 80% за 120 мин, если энергия активации равна 60 кДж/моль?

Решение. Для реакции первого порядка константа скорости выражается через степень превращения следующим образом:

,

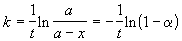
где a = x/a — степень превращения. Запишем это уравнение при двух температурах с учетом уравнения Аррениуса:

,

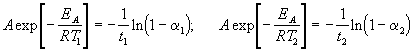
где E_A = 60 кДж/моль, T₁ = 343 K, t₁ = 60 мин, a ₁ = 0.4, t₂ = 120 мин, a ₂ = 0.8. Поделим одно уравнение на другое и прологарифмируем:

Подставляя в это выражение приведенные выше величины, находим T₂ = 333 К = 60 о С.

Пример 4-3. Скорость бактериального гидролиза мышц рыб удваивается при переходе от температуры -1.1 о С к температуре +2.2 о С. Оцените энергию активации этой реакции.

Решение. Увеличение скорости гидролиза в 2 раза обусловлено увеличением константы скорости: k₂ = 2k₁. Энергию активации по отношению констант скорости при двух температурах можно определить из уравнения (4.3) с T₁ = t₁ + 273.15 = 272.05 K, T₂ = t₂ + 273.15 = 275.35 K:

130800 Дж/моль = 130.8 кДж/моль.

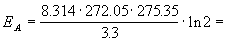
4-1. При помощи правила Вант-Гоффа вычислите, при какой температуре реакция закончится через 15 мин, если при 20 о С на это требуется 2 ч. Температурный коэффициент скорости равен 3.(ответ)

4-2. Время полураспада вещества при 323 К равно 100 мин, а при 353 К — 15 мин. Определите температурный коэффициент скорости.(ответ)

4-3. Какой должна быть энергия активации, чтобы скорость реакции увеличивалась в 3 раза при возрастании температуры на 10 0 С а) при 300 К; б) при 1000 К?(ответ)

4-4. Реакция первого порядка имеет энергию активации 25 ккал/моль и предэкспоненциальный множитель 5 . 10 13 сек -1 . При какой температуре время полураспада для данной реакции составит: а) 1 мин; б) 30 дней?(ответ)

4-5. В каком из двух случаев константа скорости реакции увеличивается в большее число раз: при нагревании от 0 о С до 10 о С или при нагревании от 10 о С до 20 о С? Ответ обоснуйте с помощью уравнения Аррениуса.(ответ)

4-6. Энергия активации некоторой реакции в 1.5 раза больше, чем энергия активации другой реакции. При нагревании от T₁ до T₂ константа скорости второй реакции увеличилась в a раз. Во сколько раз увеличилась константа скорости первой реакции при нагревании от T₁ до T₂?(ответ)

4-7. Константа скорости сложной реакции выражается через константы скорости элементарных стадий следующим образом:

Выразите энергию активации и предэкспоненциальный множитель сложной реакции через соответствующие величины, относящиеся к элементарным стадиям.(ответ)

4-8. В необратимой реакции 1-го порядка за 20 мин при 125 о С степень превращения исходного вещества составила 60%, а при 145 o C такая же степень превращения была достигнута за 5.5 мин. Найдите константы скорости и энергию активации данной реакции .(ответ)

4-9. Реакция 1-го порядка при температуре 25 о С завершается на 30% за 30 мин. При какой температуре реакция завершится на 60% за 40 мин, если энергия активации равна 30 кДж/моль?(ответ)

4-10. Реакция 1-го порядка при температуре 25 о С завершается на 70% за 15 мин. При какой температуре реакция завершится на 50% за 15 мин, если энергия активации равна 50 кДж/моль?(ответ)

4-11. Константа скорости реакции первого порядка равна 4.02 . 10 -4 с -1 при 393 К и 1.98 . 10 -3 с -1 при 413 К. Рассчитайте предэкспоненциальный множитель для этой реакции.(ответ)

4-12. Для реакции H₂ + I₂ 2HI константа скорости при температуре 683 К равна 0,0659 л/(моль. мин), а при температуре 716 К — 0,375 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 700 К.(ответ)

4-13. Для реакции 2N₂O 2N₂ + O₂ константа скорости при температуре 986 К равна 6,72 л/(моль. мин), а при температуре 1165 К — 977,0 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 1053,0 К.(ответ)

4-14. Трихлорацетат-ион в ионизирующих растворителях, содержащих H + , разлагается по уравнению

H + + CCl₃COO — CO₂ + CHCl₃

Стадией, определяющей скорость реакции, является мономолекулярный разрыв связи C- C в трихлорацетат-ионе. Реакция протекает по первому порядку, и константы скорости имеют следующие значения: k = 3.11 . 10 -4 с -1 при 90 о С, k = 7.62 . 10 -5 с -1 при 80 о С. Рассчитайте а) энергию активации, б) константу скорости при 60 о С.(ответ)

4-15. Для реакции CH₃COOC₂H₅ + NaOH ѕ CH₃COONa + C₂H₅OH константа скорости при температуре 282,6 К равна 2,307 л/(моль. мин), а при температуре 318,1 К — 21,65 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 343 К.(ответ)

4-16. Для реакции C₁₂H₂₂O₁₁ + H₂O C₆H₁₂O₆ + C₆H₁₂O₆ константа скорости при температуре 298,2 К равна 0,765 л/(моль. мин), а при температуре 328,2 К — 35,5 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 313,2 К.(ответ)

4-17. Вещество разлагается двумя параллельными путями с константами скорости k₁ и k₂. Какова разность энергий активации этих двух реакций, если при 10 o C k₁/k₂ = 10, а при 40 o C k₁/k₂ = 0.1?(ответ)

4-18. В двух реакциях одинакового порядка разница энергий активации составляет E₂ — E₁ = 40 кДж/моль. При температуре 293 К отношение констант скорости равно k₁/k₂ = 2. При какой температуре константы скорости сравняются?(ответ)

4-19. Разложение ацетондикарбоновой кислоты в водном растворе — реакция первого порядка. Измерены константы скорости этой реакции при разных температурах:

T, о С

k. 10 5 , с -1

Рассчитайте энергию активации и предэкспоненциальный множитель. Чему равен период полураспада при 25 о С? (ответ)

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

Расчеты энергии активации реакции по уравнению Аррениуса

Задача 341.
Чему равна энергия активации реакции, если при повышении температуры от 290 до 300 К скорость ее увеличится в 2 раза?
Решение:
Из уравнения Аррениуса находим:

E_a — энергия активации, k и k’ — константы скорости реакции, Т – температура в К (298). Учитывая, что происходит повышение температуры реакции от 290 К до 300 К, уравнение можно преобразовать, получим:

Ответ: 49,9кДж/моль.

Задача 342.
Каково значение энергии активации реакции, скорость которой при 300 К в 10 раз больше, чем при 280 К?
Решение:
Из уравнения Аррениуса находим:

E_a — энергия активации, k и k’ — константы скорости реакции, Т – температура в К (298). Учитывая зависимость константы скорости реакции от изменения температуры, получим:

Подставляя в последнее уравнение данные задачи и, выражая энергию активации в джоулях, получим:

Ответ: 80,3кДж/моль.

Задача 343.
Энергия активации реакции O_3(г) + NO_(г) → O_2(г) + NO_2(г) равна 10 кДж/моль. Во сколько раз изменится скорость реакции при повышении температуры от 27 до 37 °С ?
Решение:
Из уравнения Аррениуса находим:

E_a — энергия активации, k и k’ — константы скорости реакции, Т – температура в К (298). Учитывая зависимость константы скорости реакции от изменения температуры, получим:

Подставляя в последнее уравнение данные задачи и, выражая энергию активации в джоулях, получим:

Окончательно находим: k/k’ = 1,14.

Ответ: В 1,14 раз.

Задача 344.
Зависит ли температурный коэффициент скорости реакции от значения энергии активации? Ответ обосновать.
Решение:
Согласно правилу Вант-Гоффа, зависимость скорости реакции от температуры определяется уравнением:

Здесь v_t и k_t — скорость и константа скорости реакции при температуре t °С; v_{(t + 10)} и k_{(t + 10)} те же величины при температуре (t + 10 °С ); 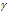— температурный коэффициент скорости реакции, значение которого для большинства реакций лежит в пределах 2 — 4 (правило Вант-Гоффа).

Возрастание скорости реакции с ростом температуры принято характеризовать температурным коэффициентом скорости реакции 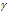— числом, показывающим, во сколько раз возрастёт скорость данной реакции при повышении температуры системы на 10 градусов. Температурный коэффициент различных реакций различен. В то же время каждая реакция характеризуется определённым барьером энергии; для его преодоления необходима энергия активации – избыточная энергия, которой должны обладать молекулы при данной температуре, для того чтобы их столкновение привело бы к образованию нового вещества. Зависимость константы скорости реакции (k) от энергиия активации (Ea кДж/моль) выражается уравнением Аррениуса: или , где

Е_а — энергия активации, k и k’ — константы скорости реакции, Т – температура в К (298). Учитывая зависимость константы скорости реакции от изменения температуры, получим:

Из чего следует, что чем меньше энергия активации и выше температура, тем больше константа скорости реакции и k’/k .

В стандартных условиях энергия активации различных реакций различна и она зависит от природы реагирующих веществ.

Таким образом, температурный коэффициент (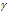) не зависит от энергия активации (E_a).

Задача 345.
Зависит ли значение энергии активации реакции в случае гетерогенного катализа от площади поверхности катализатора и от ее структуры?
Решение:
Известно, что катализатор снижает энергию активации реакции, чем дольше активность катализатора, тем большее снижение энергии активации реакции наблюдается в присутствии катализатора.

При гетерогенном катализе реакция протекает на поверхности катализатора. Отсюда следует, что активность катализатора зависит от величины поверхности (площади) его и свойств этой поверхности. Чаще всего используют пористую структуру (пемза, асбест и др.). Чтобы увеличить активность данного катализатора, нужно увеличить площадь соприкосновения его с реагентом. Применяют катализаторы с различной структурой поверхности (пористую, порошковую, в виде колец, трубок и т.п.).

Таким образом, с увеличением площади поверхности твёрдого катализатора увеличивается его активность и, соответственно, значительно уменьшается энергия активация катализируемой реакции.

Задача 346.
Реакция 2Н_2(г) + О_2(г) = 2Н₂О_(г) протекает с выделением теплоты. Однако для того, чтобы реакция началась, исходную смесь газов надо нагреть. Как это объяснить?
Решение:
Данная реакция является экзотермической, но для начала протекания реакции необходимо дополнительно подогреть смесь водорода и кислорода. Это можно объяснить тем, что энергия активации реакции слишком велика ( больше 120 кДж/моль), значит лишь только малая часть столкновений молекул водорода и кислорода друг с другом приводит к их взаимодействию. Для того чтобы увеличить число активных столкновений необходимо исходную смесь нагреть, т.е. повысить температуру системы, что вызовет разрыв или ослабление связей между атомами молекул газов. При нагревании смеси Н₂ и О₂ в отношении 2 : 1 происходит взрыв. Объясняется это тем, что из атомов водорода и кислорода, изначально образовавшихся при подогревании газовой смеси, образуются радикалы * ОН, которые легко реагируют с молекулой Н₂ с образованием молекул Н₂О и * Н. Последний реагирует с молекулой О₂ с образованием радикалов * О *, и * ОН. В свою очередь, атом кислорода, реагируя с молекулой Н₂, порождает радикалы * Н и * ОН, при столкновении которых образуется молекула Н₂О.

Таким образом, при нагревании смеси водорода и кислорода происходит увеличение образования активных частиц(* О * , *Н, *ОН), что порождает цепную реакцию, и скорость её резко возрастает, происходит взрыв смеси газов.

Видео:Использование уравнения Аррениуса для решения задач (2/2). Химия для поступающих.Скачать

Примеры решения задач. Пример 1. Установлено, что энергия активации разложения карбамида в присутствии катализатора уреазы уменьшается в четыре раза

Пример 1. Установлено, что энергия активации разложения карбамида в присутствии катализатора уреазы уменьшается в четыре раза. Оценитьпри какой температуре необходимо проводить эту же реакцию разложения, чтобы она протекала с такой же скоростью, как и каталитическая реакция при температуре 298 К?

Решение. Запишем для каталитической реакции в присутствии уреазы уравнение Аррениуса 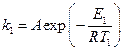, где Т₁, = 298 К;Е₁ – энергия активации.

В отсутствие уреазы это уравнение примет вид[3]:

,

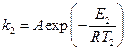
где Е₂ – энергия активации, отличная, от Е₁; Т₂ – температура, при которой k₂= k₁. Приравнивая левые части обоих уравнений, после логарифмирования получим:

, откуда .

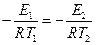
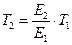
Подставляя значение 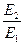= 4 (дано по условию задачи), находим: Т₂= 4·298 = 1192 К (919 °С). Таким образом, для достижения одинаковой с каталитической реакцией скорости требуется значительное повышение температуры по сравнению с 298 К, т.е. существенные затраты энергии.[4]

Пример 2. Для некоторой химической реакции присутствие катализатора позволяет уменьшить энергию активации химического процесса, реализуемого при температуре 500 °С, от 50 до 35 кДж. Покажем:

а) во сколько раз увеличится скорость каталитической реакции по сравнению с некаталитической, полагая, что все другие факторы скорости реакции остаются неизменными;

б) при какой температуре каталитическая реакция протекала бы с такой же скоростью, что и некаталитическая при 500 °С;

в) какие преимущества дает использование катализатора?

а) Пусть для некаталитической реакции уравнение Аррениуса имеет вид:

, (1)

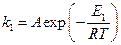
В присутствие катализатора это уравнение имеет вид:

. (2)

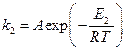
Если поделим уравнение (1) на уравнение (2), то после логарифмирования получим:

= 2,3; откуда и ;

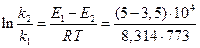
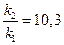
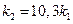
Используем уравнение Аррениуса, связывающее кинетические параметры следующим

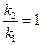
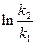
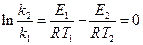
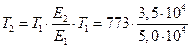
б) найдем температуру, при которой k₂будет иметь такое же значение, что и k₁при 500 °С (или 773 К). Это означает, что надо найти температуру Т₂ , для которой и = 0.

, откуда

=541,1 К(261,8) °С;

в) использование катализатора позволяет понизить температуру, не уменьшая скорости процесса, что приведет к экономии энергии (особенно это важно для промышленных процессов).

Пример 3.Экспериментально установлено, что реакция

2Се 4+ + Тl = 2Се 3+ + Т1 3+ (1)

протекает в растворе очень медленно, но ускоряется в присутствии ионов Ag + , причем скорость становится пропорциональной концентрации ионов Ag + . На основании предложенного механизма для этой реакции

Ag + + Се 4+ 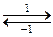Ag 2+ 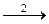+ Се 3+ , (1a)

Ag 2+ + Tl + Ag + + Tl 2+ , (2)

Tl 2+ + Се 4+ 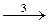Tl 3+ + Се 3+ , (3)

Необходимо вывести кинетическое уравнение для образования продукта реакции (1), ионов Т1 3+ .

Скорость образования продукта Т1 3+ можно записать как

(4)

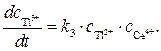
Ион Т1 2+ образуется только по стадии (2) и вступает в реакцию лишь на стадии (3), поэтому скорости этих двух стадий выравниваются, т.е.

(5)

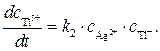
Концентрацию другого промежуточного соединения, Ag 2+ , находим, используя принцип квазистационарных концентраций:

(6)

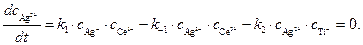
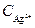
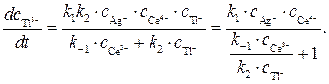
Подставляя значение из выражения (6) в уравнение (4), получим

(7)

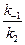
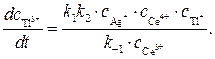
Значение отношения констант в начальный период реакции таково, что в знаменателе никакой член не является домини­рующим, это не позволяет провести аппроксимацию. Но на последних стадиях реакции первый член становится преобладающим, т.е. единицей можно пренебречь, и выражение для скорости аппроксимируется к виду

(8)

Полученное кинетическое уравнение подтверждает опытный факт прямо пропорциональной зависимости скорости образования продуктов от концентрации катализатора — ионов Ag + .

Вопросы для самоконтроля

1. Дайте классические определения терминов «катализ» и «катализатор». Являются ли теплота и свет катализаторами?

2. Оказывает ли катализатор влияние на термодинамические условия процесса? Смещает ли он положение равновесия? Может ли он изменить выход продукта реакции? Ответ объясните.

3. В чем заключается причина увеличения скорости химической реакции в присутствии катализатора?

Дата добавления: 2016-01-09 ; просмотров: 2933 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

📺 Видео

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

Решение задач на тему: "Правило Вант-Гоффа". 1 часть. 10 класс.Скачать

6 Уравнение Аррениуса, ч 2Скачать

Как температура влияет на скорость химической реакции? Уравнение АррениусаСкачать

Уравнение Аррениуса, часть 1Скачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Скорость реакции. Химия – ПростоСкачать

Порядок реакции и энергия активацииСкачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Задачи на правило Вант-Гоффа. Зависимость скорости реакции от температуры.Скачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Задачи на скорость реакции в зависимости от концентрации реагентовСкачать

Решение задач с помощью уравнений.Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Химия ПростоСкачать