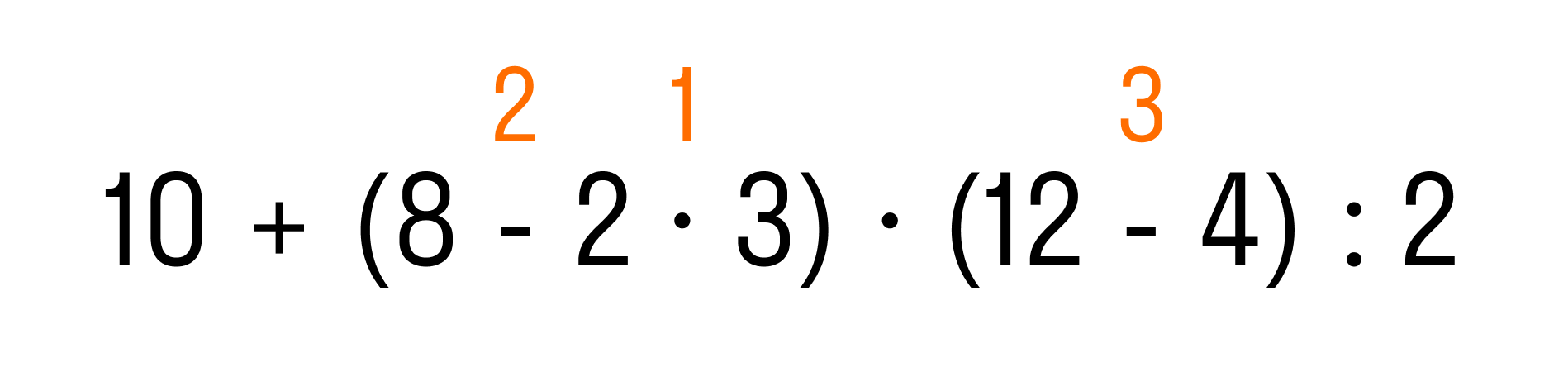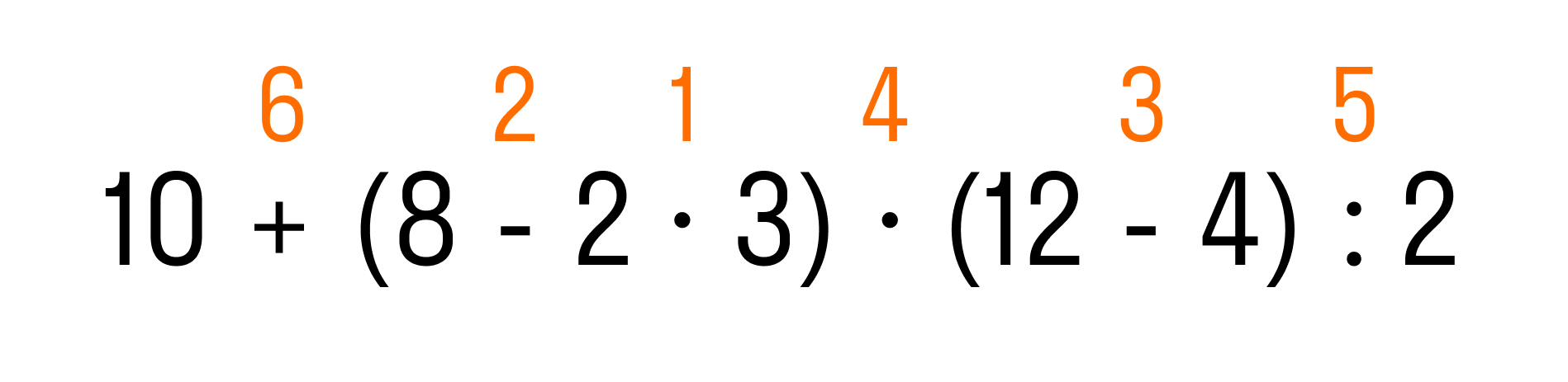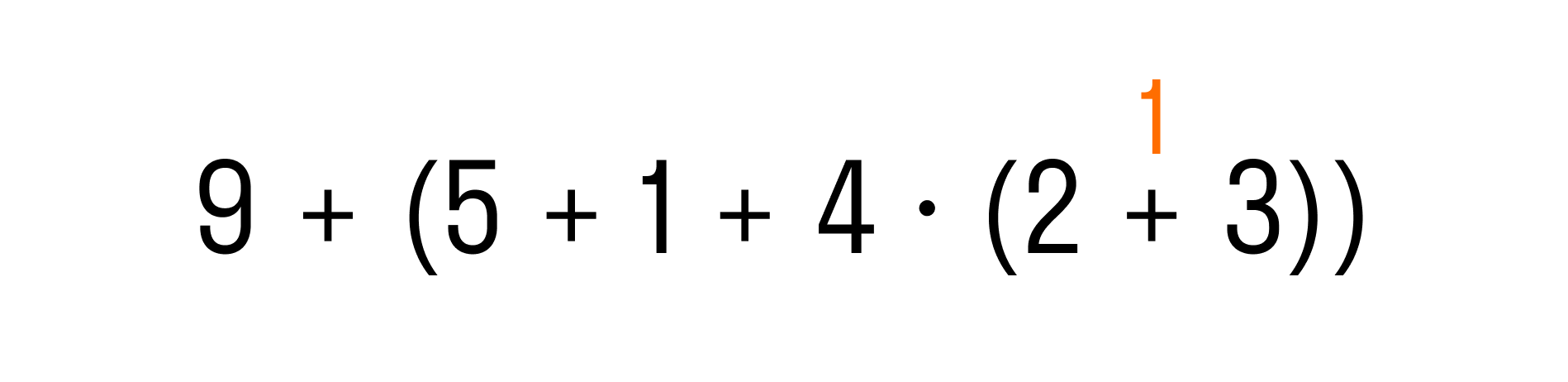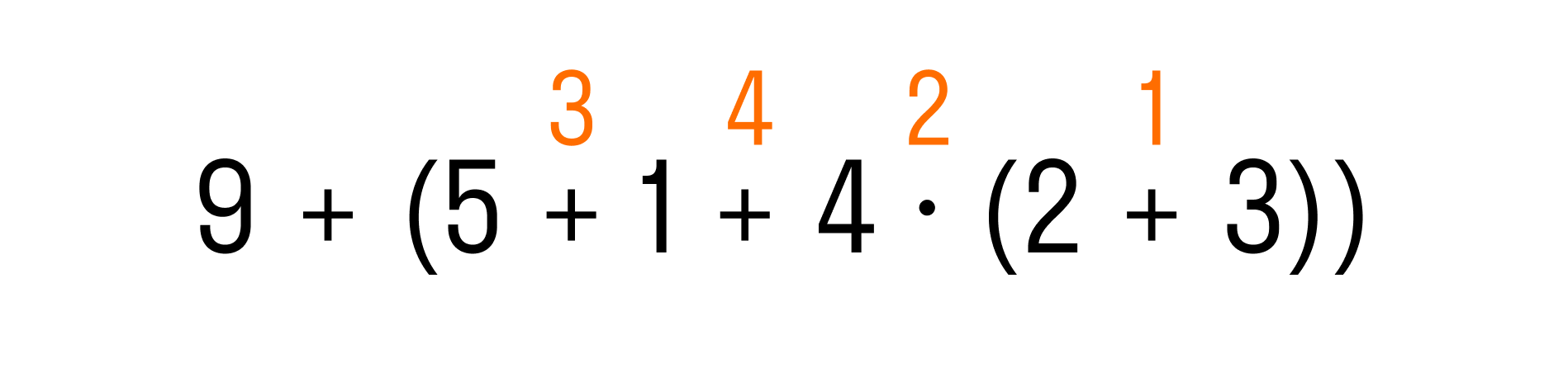Примеры уравнений на сложение и вычитание умножение и деление (2 видео)

Решение сложных уравнений. 3 класс.

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим уравнение в 2 действия:

х + 56 = 98 — 2 — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

Такое уравнение можно решить несколькими способами.

У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем — будет 30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

8 • у = 24 – это уравнение простое.

Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.

Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 59

Содержание

Примеры по действиям с многозначными числами для 4 класса
Примеры на порядок действий со скобками (сложение, вычитание, умножение, деление)
Порядок действий в математике
Основные операции в математике
Порядок вычисления простых выражений
Действия первой и второй ступени
Порядок вычислений в выражениях со скобками
🎥 Видео

Видео:Сложение и вычитание многочленов. Алгебра, 7 классСкачать

Примеры по действиям с многозначными числами для 4 класса

Подборка примеров со скобками на порядок действий для отработки вычислительных навыков.

Цель: формирование умения определять порядок выполнения действий в числовых выражениях со скобками.

Данную подборку примеров на порядок действий можно для удобства разделить на карточки по 5 штук. Чтобы достичь хороших результатов каждый день нужно решать именно такое количество. Ответы на примеры с многозначными числами даны для самоконтроля учащихся.

Ранее мы разбирали алгоритм решения примеров на порядок действий в 3-4 классе со скобками и без.

Вспомним алгоритм решения примеров на порядок действий со скобками:

Главное правило: если в примере есть скобки, то сначала выполняем действия в скобках, затем умножение и деление, и потом — сложение и вычитание начиная слева направо.

При решении примера сначала избавьтесь от скобок.
Вычислите и запишите полученный результат на месте скобок.
Выполните действия по порядку.

Разберем порядок вычисления примера со скобками пошагово:

Пример

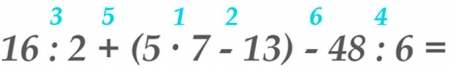
Определим порядок действий и запишем их над арифметическими знаками.
Найдём значение выражения, заключённого в скобках: сначала умножение или деление, потом сложение или вычитание слева направо.
Приступим к действиям вне скобок/можно решать одновременно.

16 : 2 + (5 ⋅ 7 – 13) – 48 : 6 = 8 + (35 – 13) – 8 = 8 + 22 – 8 = 22.

Примеры на порядок действий со скобками (сложение, вычитание, умножение, деление)

Задание: расставь порядок действий и найди значение выражения.

9464 : 91 + (926 * 50 – 9601) =
3091 – 9 * (161 + 42) + 1791 =
(349 + 636 : 6) + 9914 – 412 =
(2340 : 5 + 932) : 50 =
801 + (8049 – 818) * 4 =
3402 + (1334 : 23 + 7026) =
81 * 13 + (6043 – 5711) : 2 =
71 * 38 + (322 * 2 + 7011) =
(744 + 256) : 50 + 724 =
(1561 + 2810) – (2004 + 2330 : 5) =
550 : (610 – 555) + 292 * 31 =
(859 + 99) – 141 * 5 + 200 =
71 * 265 – (1554 : 74 + 375) =
(2011 + 9411) + 6633 : 33 =
462 : (560 – 546) * 27 + 521 =
1908 : 12 * (1093 – 809) =
(6105 : 5 — 450) + 613 – 105 =
964 + (6643 – 5963) * 155 =
112 * 49 – (1478 + 2411) – 322 =
9726 – (1430 – 86) : 42 – 2016 =
1390 : (528 – 518) + (9493 + 185) =
3012 + (3010 – 2110) * 6 + 411 =
8505 : 21 + (1585 – 914) : 61 =
351 * 0 + (1137 + 9120) : 3 =
(7196 – 1750) + (5310 : 5 + 2822) =
(4278 : 93 + 924 : 42) + 631 =
714 : 7 + (9756 – 4197) : 3 =
(5861 + 14) : 25 + (234 + 390) =
(1117 + 3250) – 132 * 13 =
(96 * 214 – 14) + (4126 + 54) : 2 =

Ответы на примеры по действиям с многозначными числами:

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Порядок действий в математике

О чем эта статья:

Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Основные операции в математике

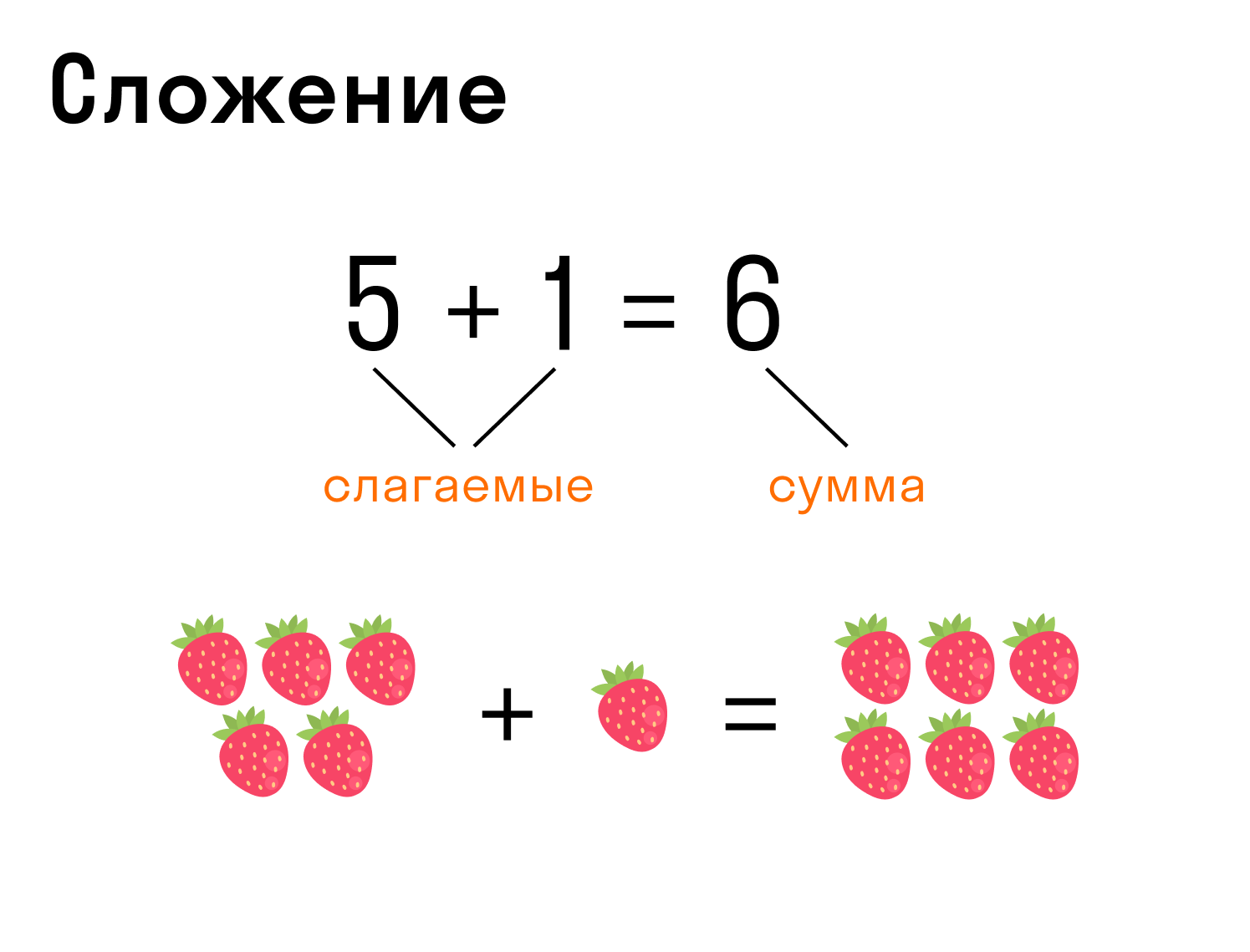
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше ( );

меньше (

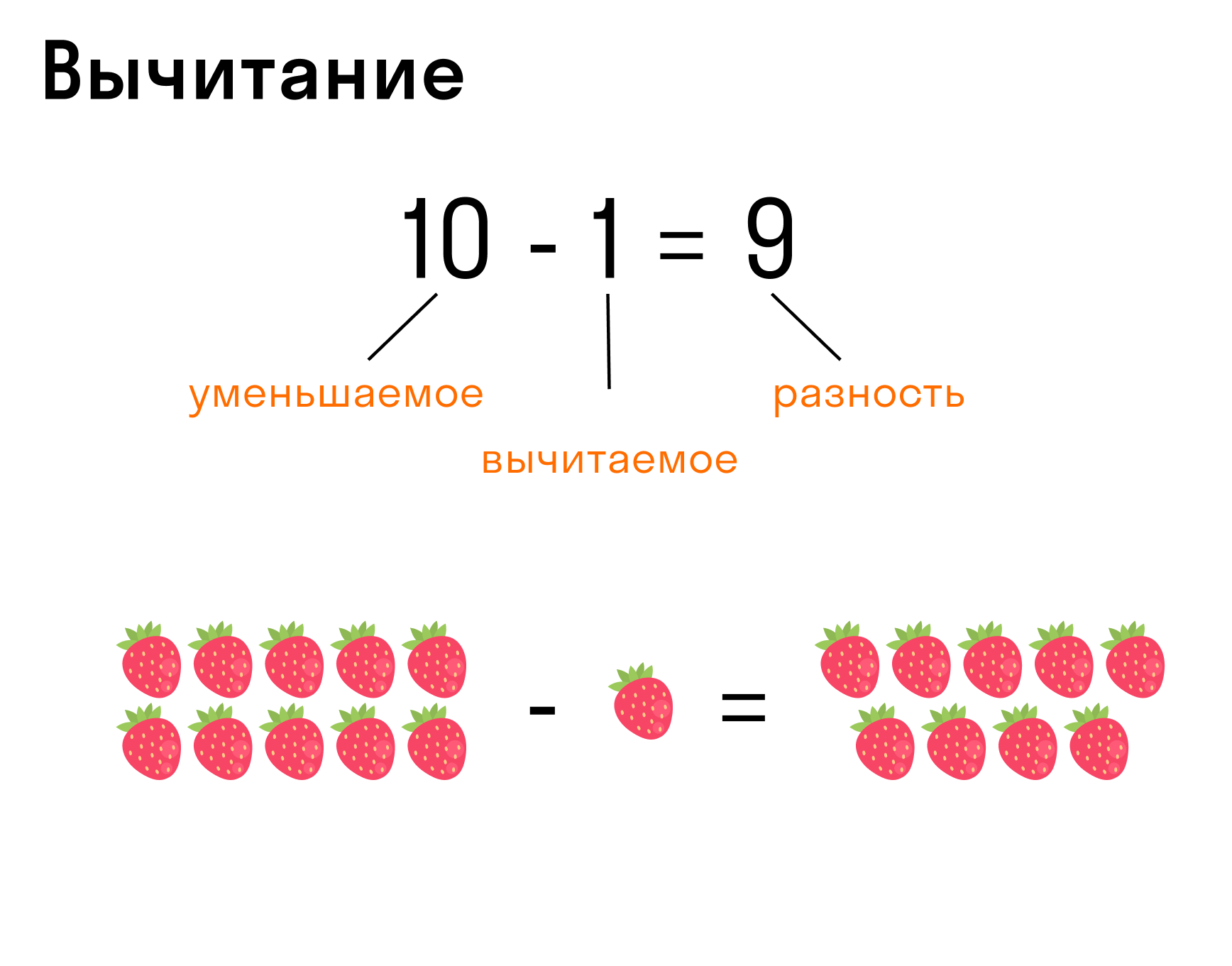
Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

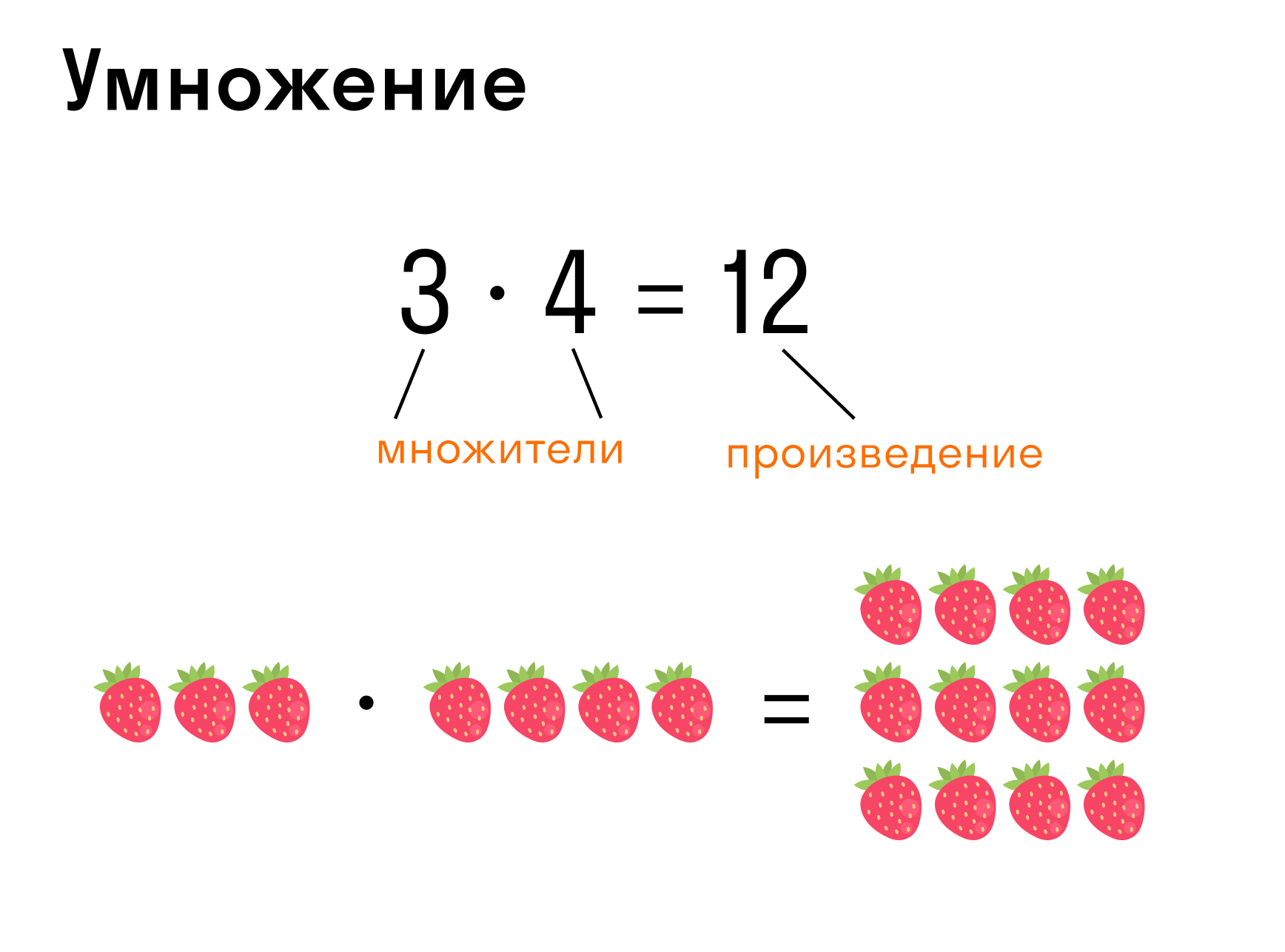
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.

3 × 4 = 3 + 3 + 3 + 3, то есть число 3 сложили 4 раза само с собой.

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 × 2 = 5 + 5 = 10 и 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10.

Поэтому и множитель, и множимое называют сомножителями.

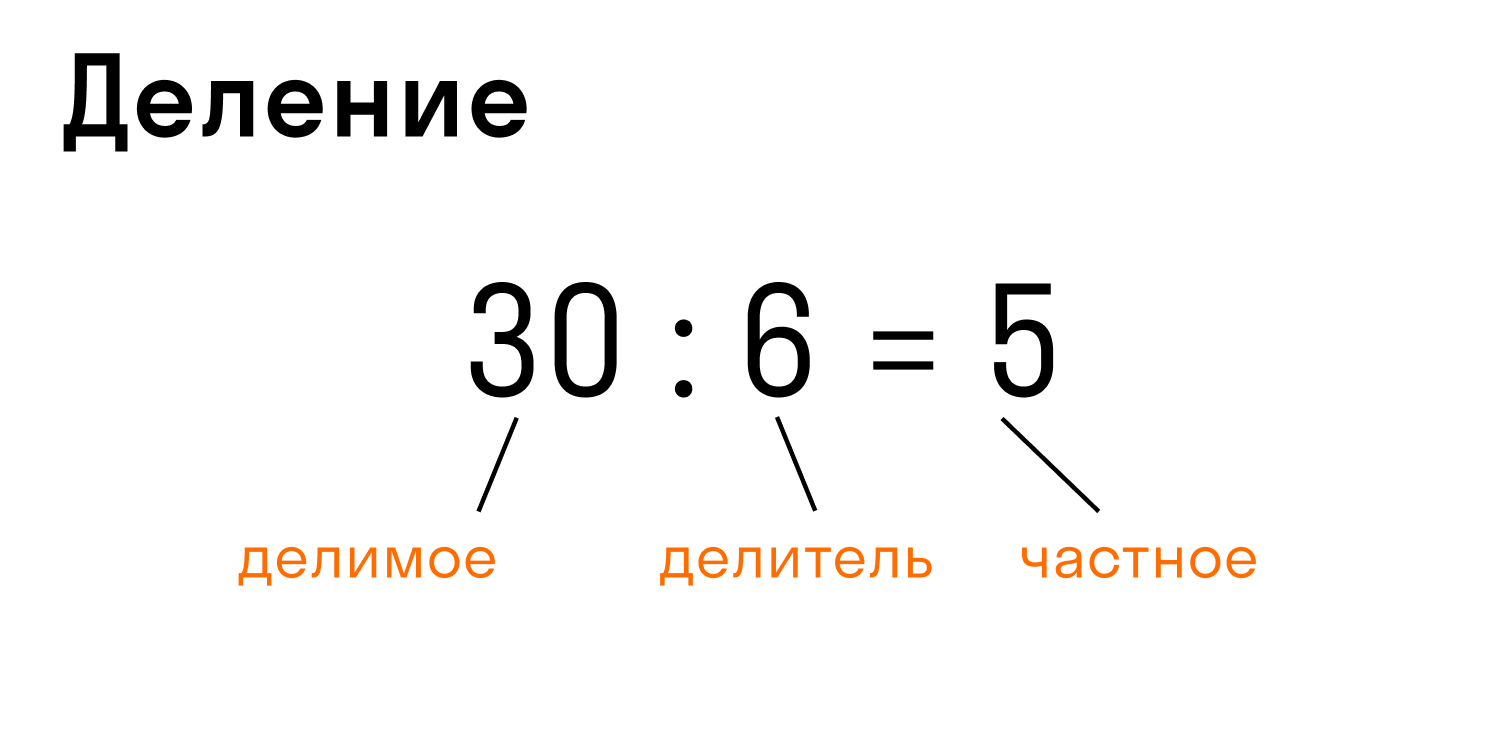
Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5 в качестве проверки дает делимое 30.

Сложение и вычитание, умножение и деление попарно представляют обратные друг другу действия. А теперь давайте узнаем порядок выполнения арифметических действий.

Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

действия выполняются по порядку слева направо

сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11 − 2 + 5.

В нашем выражении нет умножения, деления и скобок, поэтому выполняем все действия слева направо. Сначала вычтем два из одиннадцати:

Затем прибавим к результату пять и в итоге получим четырнадцать:

Вот запись всего решения: 11 − 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 × 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два:

Теперь результат умножаем на семь:

И получившееся в число делим на пять:

Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Видео:8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?Скачать

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 − 2 × 3) × (12 − 4) : 2.

Как правильно решить пример:

Сначала определим порядок действий. Выражение содержит скобки, поэтому сначала будем выполнять действия в выражениях, которые заключены в эти скобки.

Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание.

Итак, мы определили первые три действия:

Когда выполнены все действия в скобках, по правилу дальше мы должны выполнить умножение и деление, и в последнюю очередь — сложение. Теперь мы знаем, в каком порядке решать пример:

Осталось решить пример по действиям:

2 × 3 = 6
8 − 6 = 2
12 − 4 = 8
2 × 8 = 16
16 : 2 = 8
10 + 8 = 18

На этом все действия выполнены.

Ответ: 10 + (7 − 2 × 3) × (12 − 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 × (2 + 3)).

Для начала определим порядок действий

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 × (2 + 3). Но это выражение также содержит скобки, поэтому начнем сначала с действий в них: