Решение задач. 10-й класс. Базовый курс
Предлагаемые два варианта заданий можно использовать при проведении урока с элементами коллективного и индивидуального соревнований, а также для зачетов. На уроке я делю класс на две команды. Вначале каждый участник пытается решить посильное самостоятельно, затем под руководством капитанов – в группе. Разрешается совещаться и обращаться с вопросами ко мне. В конце урока за индивидуальную работу ставится оценка (зачет).
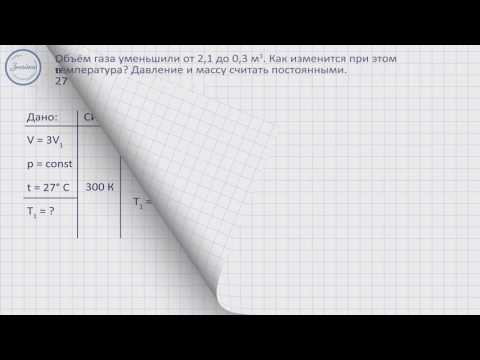
1. Баллон емкостью 0,0831 м 3 содержит 1,6 кг кислорода. При какой температуре баллон может разорваться, если он выдерживает давление 2 • 10 6 Па?
2. Баллон, наполненный газом под давлением 2,84 МПа, находился на складе при температуре 7 °С. После того как половину газа израсходовали, баллон внесли в помещение. Какова температура в помещении, если давление газа в баллоне через некоторое время стало 1,52 МПа?
4. Определите молярную массу углекислого газа.
5. Прибор для измерения давления газа
6. Почему нагретая медицинская банка «присасывается» к телу человека?
7. Найдите ошибки:
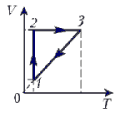
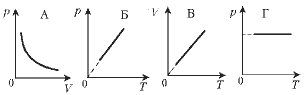
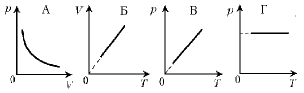
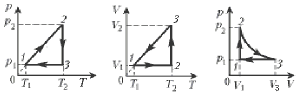
8. Какой график отражает закон Шарля?
9. Выразите величину V и проверьте правильность полученных единиц ее измерения:
V = 0,0831 м 3 ,
m = 1,6 кг,
M(O2) = 32 • 10 –3 кг/моль,
p = 2 • 10 6 Па.
_______________
T – ?
3. 1–2 – изотермический (расширение); 2–3 – изохорный (нагревание); 3–1 – изобарный (сжатие).
4. M(CO2) = (12 + 32) • 10 –3 = 44 • 10 –3 (кг/моль).
6. При нагревании воздуха в банке часть его выходит, так что при охлаждении давление в банке становится меньше атмосферного.
1. Определите массу углекислого газа, находящегося в баллоне емкостью 5 • 10 –2 м 3 при температуре 300 К. Давление газа 3 • 10 6 Па.
2. В сварочном цехе стоит 50 баллонов ацетилена (С2Н2) емкостью 40 л каждый. Все баллоны включены в общую магистраль. После 10 ч непрерывной работы давление во всех баллонах упало с 1,2 • 10 6 до 5 • 10 5 Па. Найдите средний расход ацетилена за секунду, если температура в цехе оставалась неизменной и равнялась 27 °С.
4. Определите молярную массу серной кислоты (H2SO4).
5. Прибор для измерения параметра состояния термодинамической системы.
6. Почему у глубоководных рыб плавательный пузырь выходит через рот наружу, если их извлечь из воды?
7. Найдите ошибки:
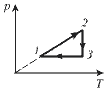
8. Какой график отражает закон Гей-Люссака?
9. Выразите величину р и проверьте правильность получаемых единиц ее измерения:
V = 5 • 10 –2 м 3 ,
T = 300 К,
p = 3 • 10 6 Па,
M(СО2) = 44 • 10 –3 кг/моль.
_________________
m – ?
M(C2H2) = 26 • 10 –3 кг/моль,
N = 50,
V1 = 40 л, СИ: 0,04 м 3
t = 10 ч, СИ: 36 • 10 3 с
p1 = 1,2 • 10 6 Па,
p2 = 5 • 10 5 Па,
t = 27 °С. СИ: T = 300 К
_____________


3. 1–2 – изохорный (нагревание); 2–3 – изотермический (расширение); 3–1 – изобарный (сжатие).
6. Давление на большой глубине намного превышает атмосферное, поэтому плавательный пузырь при подъеме рыбы значительно увеличивается в объеме.
7.
Видео:Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать
Решение задач по теме «Уравнение состояния идеального газа»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
311 лекций для учителей,
воспитателей и психологовПолучите свидетельство
о просмотре прямо сейчас!ТЕМА: Решение задач по теме «Уравнение состояния идеального газа»
Учебная: Диагностика степени усвоения знаний по теме «Уравнение состояния идеального газа» и формирование практических умений по их применению .
Развивающая: Развивать интерес к физике, развивать практические умения учащихся при решении задач.
Воспитательная : воспитывать сознательное отношение к учебе и заинтересованность в изучении физики.
Тип урока: урок комплексного применения знаний
I. Организационно — мотивационный этап
1) Организация начала урока
2) Проверка домашнего задания
II. Организационно — мотивационный этап
3) Актуализация имеющихся знаний.
4) Закрепление знаний и способов действия
6) Первоначальная проверка понимания
III. Рефлексийна — заключальны этап
7) Подведение итогов занятия. Выставление оценок
8) Домашнее задание
I. Организационно — мотивационный этап
1) Организация начала урока
Приветствие учащихся и учителя. Проверить подготовленность учащихся к уроку, правильную организацию рабочего места. Отметить отсутствующих в журнале.
2) Проверка домашнего задания
Фронтальная проверка выполнения домашнего задания. Обсуждения результатов выполнения
II. Операционно — познавательный этап.
3) Актуализация имеющихся знаний.
А) Фронтальный опрос
— Перечислите макроскопические параметры состояния идеального газа ( Р,V,Т)
— Какое уравнение называют уравнением состояния? (Уравнение, выражающее связь между макроскопическими параметрами состояния вещества)
-В чем заключается основная задача МКТ? ( Установление связи между макроскопическими параметрами, т.е. нахождение уравнения состояния того или иного тела)
-Сформулировать и доказать закон Дальтона (Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов, p=p1 +…рn )
-Записать уравнение Клапейрона. При каких условиях оно справедливо? (PVT=P0V0\T0, m=const, M=const)
— Записать уравнение Менделеева — Клапейрона.
4) Закрепление знаний и способов действия
Задачи решаются на доске:
1. Определить массу водорода, находящегося в баллоне вместимостью 20 л при давлении 830 кПа, если температура газа равна 17 °С.
Дано: V = 20 л, р = 830 кПа, t = 17 ° C , М = 2·10-3 кг/моль, R = 8,31 Дж/(моль·К).
Решение
Выведем размерность искомой физической величины:
Ответ: m = 1,38·10 -2 кг.
2 . Газ при давлении 0,2 МПа и температуре 15 0 С имеет объем 5 л. Чему будет равен объем этой массы газа при нормальных условиях?
3. В баллоне находится газ под давлением 40 Па и при температуре 27 °С. Когда из баллона выпустили 3/5 газа, содержавшегося в нем, его температура понизилась до -33 °С. Определить давление газа, оставшегося в сосуде.
Дано: V — const , р1 = 40 МПа, t 1 = 27 °С, t 2 = -33 °С, m 2 = 2/5 m 1
Решение
Ответ: р2 = 12,8 Па.
4. При уменьшении объема газа в 2 раза давление увеличилось на 120 кПа, а абсолютная температура возросла на 10 %. Каким было первоначальное давление?
6) Первоначальная проверка понимания
Задачи решаются самостоятельно учениками
1. Определите температуру кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении 5 • 10 6 Па. Молярная масса кислорода М = 0,032 кг/моль.
Р е ш е н и е. Согласно уравнению Менделеева—Клапейрона
Отсюда температура
кислорода.
2. Найти плотность водорода при температуре 15 0 С и давлении 9,8·10 4 Па. (0,085 кг/м 3 )
3. В баллоне находится газ при температуре 15 0 С. Во сколько раз уменьшится давление газа, если 40 % его выйдет из баллона, а температура при этом понизится на 8 0 С?
( Ответы : m=16 кг ; Р =249300 Па ; V=0,03 м 3; Т =150 К )
III. Рефлексийно – заключительный этап
7) Подведение итогов занятия. Выставление оценок
8) Домашнее задание упр.3(5-7). Подготовится к проверочной работе
9) Рефлексия: Ребята высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске: Сегодня я узнал… Было интересно… Было трудно… Я понял, что…
Решение задач по теме «Уравнение состояния идеального газа»
1. Определить массу водорода, находящегося в баллоне вместимостью 20 л при давлении 830 кПа, если температура газа равна 17 °С.
2 . Газ при давлении 0,2 МПа и температуре 15 0 С имеет объем 5 л. Чему будет равен объем этой массы газа при нормальных условиях?
3. В баллоне находится газ под давлением 40 Па и при температуре 27 °С. Когда из баллона выпустили 3/5 газа, содержавшегося в нем, его температура понизилась до -33 °С. Определить давление газа, оставшегося в сосуде.
4. При уменьшении объема газа в 2 раза давление увеличилось на 120 кПа, а абсолютная температура возросла на 10 %. Каким было первоначальное давление?
1. Определите температуру кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении 5 • 10 6 Па. Молярная масса кислорода М = 0,032 кг/моль.
2. Найти плотность водорода при температуре 15 0 С и давлении 9,8·10 4 Па. (0,085 кг/м 3 )
3. В баллоне находится газ при температуре 15 0 С. Во сколько раз уменьшится давление газа, если 40 % его выйдет из баллона, а температура при этом понизится на 8 0 С?
Решение задач по теме «Уравнение состояния идеального газа»
1. Определить массу водорода, находящегося в баллоне вместимостью 20 л при давлении 830 кПа, если температура газа равна 17 °С.
2 . Газ при давлении 0,2 МПа и температуре 15 0 С имеет объем 5 л. Чему будет равен объем этой массы газа при нормальных условиях?
3. В баллоне находится газ под давлением 40 Па и при температуре 27 °С. Когда из баллона выпустили 3/5 газа, содержавшегося в нем, его температура понизилась до -33 °С. Определить давление газа, оставшегося в сосуде.
4. При уменьшении объема газа в 2 раза давление увеличилось на 120 кПа, а абсолютная температура возросла на 10 %. Каким было первоначальное давление?
1. Определите температуру кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении 5 • 10 6 Па. Молярная масса кислорода М = 0,032 кг/моль.
2. Найти плотность водорода при температуре 15 0 С и давлении 9,8·10 4 Па. (0,085 кг/м 3 )
3. В баллоне находится газ при температуре 15 0 С. Во сколько раз уменьшится давление газа, если 40 % его выйдет из баллона, а температура при этом понизится на 8 0 С?
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать
Примеры решения задач по теме уравнение состояния идеального газа 10 класс
Репетитор
по физикеРепетитор
по алгебре( P ) — Давление газа (Паскали)
( nu ) — Количество вещества
( R ) — Универсальная газовая посиоянная
( T ) — Температура в Кельвинах
В баллоне находится газ под давлением (P= 8,31 cdot 10^6 ; Па ), температура газа (T=300 К ).
Количество вещества газа ( nu=100 Моль ).
Найти объем баллона
Универсальная газовая постоянная ( R=8,31 frac )
Дать ответ в литрах.
Показать ответ Показать решение ВидеорешениеЗапишем уравнение Менделеева-Клапейрона :
Видео:Уравнение состояния идеального газа. 10 класс.Скачать
Задачи на газовые законы
методическая разработка по физике (10 класс) на тему
В данной работе предлагается определенный подход к классификации и способам решения задач на газовые законы. Такой подход позволит быстро сориентироваться в большом количестве задач на свойства газов и применить к ним те или иные приемы решения.
Видео:Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать
Скачать:
Вложение Размер algoritmy_resheniya_zadach_po_mkt.docx 213.89 КБ Видео:10 класс, 4 урок, Уравнение состояния идеального газаСкачать
Предварительный просмотр:
В данной работе предлагается определенный подход к классификации и способам решения задач на газовые законы. Такой подход позволит быстро сориентироваться в большом количестве задач на свойства газов и применить к ним те или иные приемы решения.
Основные теоретические сведения
Состояние газа характеризуется совокупностью трех физических величин или термодинамических параметров: объемом газа V, давлением Р и температурой Т. Состояние газа, при котором эти параметры остаются постоянными считают равновесным состоянием. В этом состоянии параметры газа связаны между собой уравнением состояния. Самый простой вид уравнение состояния имеет для идеального газа. Идеальным газом называют газ, молекулы которого не имеют размеров (материальные точки) и взаимодействуют друг с другом лишь при абсолютно упругих соударениях (отсутствует межмолекулярное притяжение и отталкивание). Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше размеры их молекул (т.е. газ одноатомный), и чем больше он разряжен.
Уравнение состояния идеального газа или уравнение Менделеева-Клапейрона имеет вид:
— универсальная газовая постоянная
Из этого закона вытекает, что для двух произвольных состояний газа справедливо равенство, называемое уравнением Клапейрона:
Так же для идеальных газов имеют место следующие экспериментальные законы:
Закон Бойля — Мариотта :
Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд.
Р = Р 1 + Р 2 +. + Р N
Задачи, решение которых основывается на данных уравнениях, можно разделить на две группы:
- задачи на применение уравнения Менделеева-Клапейрона.
- задачи на газовые законы.
ЗАДАЧИ НА ПРИМЕНЕНИЕ УРАВНЕНИЯ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА.
Уравнение Менделеева-Клапейрона применяют тогда, когда
- дано только одно состояние газа и задана масса газа (или вместо массы используют количество вещества или плотность газа).
- масса газа не задана, но она меняется, то есть утечка газа или накачка.
При решении задач на применение равнения состояния идеального газа надо помнить:
- если дана смесь газов, то уравнение Менделеева-Клапейрона записывают для каждого компонента в отдельности. Связь между парциальными давлениями газов, входящих в смесь и результирующим давлением смеси, устанавливается законом Дальтона.
- если газ меняет свои термодинамические параметры или массу, уравнение Менделеева-Клапейрона записывают для каждого состояния газа в отдельности и полученную систему уравнений решают относительно искомой величины.
- Необходимо пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.
- В задачах, где рассматривается движение сосуда с газом (пузырька воздуха, воздушного шара) к уравнению газового состояния добавляют уравнения механики.
- если между газами происходит реакция, то надо составить уравнение реакции и определить продукты реакции
ПЕРВЫЙ ТИП ЗАДАЧ: НЕТ ИЗМЕНЕНИЯ МАССЫ
- Определить давление кислорода в баллоне объемом V = 1 м 3 при температуре t=27 °С. Масса кислорода m = 0,2 кг .
Записываем уравнение Менделеева-Клапейрона и находим из него давление, производимое газом:
- Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.
Записываем уравнение Менделеева-Клапейрона и находим массу газа
- При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м 3 . Определить молярную массу газа.
Записываем уравнение Менделеева-Клапейрона
Так как масса газа может быть определена через плотность газа и его объем имеем:
Отсюда находим молярную массу газа:
- Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.
Нормальное атмосферное давление – это давление, равное 10 5 Па. И эту информацию запишем как данные задачи. Записываем уравнение Менделеева-Клапейрона
Так как масса газа может быть определена через плотность газа и его объем имеем:
Отсюда находим плотность газа:
- До какой температуры Т 1 надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре Т 2 = 200 К?
Записываем уравнение Менделеева-Клапейрона для кислорода и для водорода через плотности газов:
Так как по условию давление у двух газов одинаковое, то можно приравнять правые части данных уравнений:
Сократим на R и на плотность ρ (по условию плотности газов равны) и найдем Т 1
- В сосуде объемом 4·10 -3 м 3 находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10 -6 кг /см 3 , если давление газа остается неизменным.
ρ 2 =6·10 -6 кг /см 3
- В баллоне объемом 25 литров находится 20 г азота и 2 г гелия при 301К. Найдите давление в баллоне.
μ 1 = 0,028кг/моль
μ 2 = 0,004кг/моль
Записываем уравнение Менделеева для каждого газа и находим из него давление газов
По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений газов:
- Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?
μ 1 = 0,002кг/моль
μ 2 = 0,032кг/моль
По закону Дальтона:
- Сосуд емкостью 2V разделен пополам полупроницаемой перегородкой. В одной половине находится водород массой m В и азот массой m А . В другой половине вакуум. Во время процесса поддерживается постоянная температура Т. Через перегородку может диффундировать только водород. Какое давление установиться в обеих частях сосуда?
m 1 = m 2 = m 3 = m
Диффундирует только водород. Следовательно, после завершения установочных процессов, в отсеке I будет водород, массой на
половину меньшей, чем была, и весь азот. А во втором отсеке только половина массы водорода. Тогда для первого отсека установившееся давление равно:
Для отсека II можно так же определить установившееся давление:
- Вакуумированный сосуд разделен перегородками на три равных отсека, каждый объемом V. В средний отсек ввели одинаковые массы кислорода, азота и водорода. В результате чего давление в этом отсеке стало равно Р. Перегородка I проницаема только для молекул водорода, перегородка II проницаема для молекул всех газов. Найти давления Р 1 Р 2 и Р 3 , установившиеся в каждом отсеке, если температура газа поддерживается постоянной и равной Т.
m 1 = m 2 = m 3 = m
После диффундирования газов через перегородки в первом отсеке окажется треть массы водорода. Во втором и в третьем отсеках будет треть водорода, половина массы кислорода и половина всей массы азота. Тогда для первого отсека установившееся давление равно:
Если до диффундирования первоначальное давление во втором отсеке было Р, то можно записать:
Отсюда можно найти
Находим выражение для давления во втором и в третьем отсеках
И тогда давление в первом отсеке равно:
С химическими реакциями
- В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно Р (диссоциацией водорода можно пренебречь). При температуре 2Т, когда оба газа полностью диссоциированы, давление в сосуде 3Р. Каково отношение масс азота и водорода в смеси?
При температуре Т параметры газов в сосуде следующие:
И результирующее давление в сосуде по закону Дальтона равно:
При температуре 2Т параметры газов в сосуде следующие:
И результирующее давление в сосуде по закону Дальтона равно:
- В герметично закрытом сосуде находится 1 моль неона и 2 моля водорода. При температуре Т 1 =300К, когда весь водород молекулярный, атмосферное давление в сосуде Р 1 =10 5 Па. При температуре Т 2 =3000К давление возросло до Р 2 =1,5∙10 5 Па. Какая часть молекул водорода диссоциировала на атомы?
При температуре Т 1 давление газа в сосуде складывается из парциальных давлений двух газов и равно:
При температуре Т 2 давление газа равно:
Из первого находим объем V:
- В закрытом баллоне находится смесь из m 1 = 0,50 г водорода и m 2 = 8,0 г кислорода при давлении Р 1 = 2,35∙10 5 Па. Между газами происходит реакция с образованием водяного пара. Какое давление Р установится в баллоне после охлаждения до первоначальной температуры? Конденсации пара не происходит.
В сосуде будет происходить реакция водорода с кислородом с образованием воды:
Из уравнения реакции видно, что если в реакцию вступит весь водород, то кислорода только половина
В результате образуется ν 3 =0,25 молей водяного пара и останется ν 4 = 0,125молей кислорода.
По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений
Так как известно, что до реакции давление в сосуде было Р 1 , то для этого момента можно так же применить закон Дальтона:
Решаем полученные уравнение в системе относительно неизвестного:
С добавлением законов механики.
- На дне сосуда, заполненного воздухом, лежит шарик радиусом r и массой m. До какого давления надо сжать воздух в сосуде, чтобы шарик поднялся вверх. Температура воздуха Т известна.
Запишем уравнение динамики и уравнение Менделеева-Клапейрона. Решаем полученную систему уравнений относительно неизвестного:
- Тонкостенный резиновый шар массой 50г наполнен азотом и погружен в озеро на глубину 100 м. Найти массу азота, если шар находится в положении равновесия. Атмосферное давление 760мм. рт. ст. Температура воды в озере на глубине 100м равна 4°С.
Запишем второй закон Ньютона в проекции на вертикальную ось.
Объем шара равен объему азота в нем. Запишем уравнение Менделеева-Клапейрона для азота и выразим из него объем азота
Давление азота на этой глубине равно давлению внешнему на шар, так как по условию оболочка шара не пульсирует. Следовательно:
- Надувной шарик, заполненный гелием, удерживают на нити. Найдите натяжение нити, если масса оболочки шарика 2г, объем 3литра, давление гелия 10 5 Па, температура 27°С. Плотность воздуха 1,3 кг/м 3
μ гел =0,004кг/моль
μ воз =0,029 кг/моль
Запишем второй закон Ньютона в проекции на вертикальную ось х.
Объем шара равен объему гелия в нем, а значит 3литра; Запишем уравнение Менделеева-Клапейрона для воздуха (среда, в которой находится шар), и введем в него плотность воздуха:
Тогда уравнение (1) принимает вид:
Теперь надо записать уравнение Менделеева-Клапейрона для гелия и выразить из него массу гелия. Надо учесть, что объем азота равен объему шара. А так же температура окружающего воздуха и температура гелия равны, как равны и давления воздуха и гелия.
С учетом определенной массы гелия, сила натяжения равна:
- В вертикально расположенном цилиндре находится кислород массой m = 64 г, отделенный от атмосферы поршнем, который соединен с дном цилиндра пружиной жесткостью k = 830 H/м. При температуре T 1 = 300 К поршень располагается на расстоянии h = 1 м от дна цилиндра. До какой температуры T 2 надо нагреть кислород, чтобы поршень расположился на высоте H = 1,5м от дна цилиндра? Универсальная газовая постоянная R= 8,31 Дж/(моль∙ К), молярная масса кислорода μ = 32 г/моль.
Поскольку в условии задачи не сказано, что поршень невесом, будем полагать, что он обладает некоторой массой, которую обозначим через m 0 . Ничего не говорится также про атмосферное давление, поэтому будем считать, что оно равно Р 0 Таким образом, на поршень действуют в общем случае четыре силы: сила тяжести, сила упругости пружины, сила атмосферного давления, направленные вниз, и сила давления газа в цилиндре, направленная вверх. Условия равновесия поршня в начальном и конечном состояниях имеют вид:
Здесь через Р 1 и через Р 2 обозначено давление газа в первом и во втором состояниях. Через х 1 и х 2 обозначена деформация пружины в двух состояниях.
Вычтем из второго уравнения первое уравнение:
Запишем уравнение Менделеева-Клапейрона для двух состояний газа:
Приравняем разности давлений газа, найденные двумя способами:
Из полученного уравнения находим Т 2 :
ВТОРОЙ ТИП ЗАДАЧ: ЕСТЬ ИЗМЕНЕНИЯ МАССЫ
- Температуру воздуха в комнате подняли с t 1 = 7 °С до t 2 = 27 °С. Какая масса воздуха должна выйти из комнаты, чтобы давление осталось неизменным, Р = 10 5 Па? Объем воздуха в комнате V = 50 м 3 .
Так как при нагревании все тела расширяются, а комната не герметична, следовательно, масса воздуха в комнате при нагревании уменьшается (есть утечка газа), но при этом, понятно, что объем газа не меняется и остается равным объему комнаты. Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в комнате при разной температуре.
- Стеклянная колба закрыта пробкой и взвешена при температуре t 1 = 15 °С. Открыв пробку, колбу нагрели до температуры t 2 = 80 °С. При следующем взвешивании масса колбы оказалась на m = 0,25 г меньше. Чему равен объем колбы?
Масса стеклянной колбы не меняется, меняется масса газа в ней, так как есть утечка: при нагревании все тела расширяются, а колба не герметична, следовательно, масса воздуха в ней при нагревании уменьшается, но при этом, понятно, что объем газа не меняется и остается равным объему колбы. Будем считать, что атмосферное давление нормальное.
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в колбе при разной температуре.
Выразим отсюда объем колбы:
- В баллоне емкостью V = 12 л находится азот массой m 1 = 1,5 кг при температуре t 1 = 37°С. Каким станет давление в баллоне при температуре t 2 =50 °С, если выпустить 35% азота? Первоначальное давление считать нормальным.
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона.
- В сосуде объемом V = 1 л находится идеальный газ. В сосуде объемом V = 1 л находится идеальный газ. Сколько молекул газа нужно выпустить из сосуда, чтобы при понижении температуры в k=2 раза его давление уменьшилось в z =4 раза?
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона.
- Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура на 20%. Какую часть газа выпустили?
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона.
- В сосуде объемом V = 0,5 л находится идеальный газ при давлении Р 1 =1 атм. и температуре t = 27 °С. Сколько молекул газа нужно выпустить из сосуда, чтобы давление в нем уменьшилось в 2 раза? Температура газа не изменяется.
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона.
- В пустой сосуд объемом V нагнетают воздух при помощи поршневого насоса, объем цилиндра которого V 0 . Каким будет давление воздуха в сосуде после N качаний?
Задачи про насосы решаются так же на основе уравнения Менделеева-Клапейрона. Надо записать уравнение для накаченной массы, то есть той, что поступила в сосуд. И так же записать уравнение Менделеева-Клапейрона для газа, поступающего в рабочий резервуар насоса. И учесть, что вся масса газа, попавшая в сосуд – это масса газа, попадавшая в резервуар насоса N раз. Будем считать, что в насос газ поступает при атмосферном давлении
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в цилиндр насоса:
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в сосуд:
Поделим второе уравнение на первое:
- Компрессор засасывает из атмосферы каждую секунду 3 литра воздуха, которые подаются в баллон емкостью 45 литров. Через сколько времени давление в баллоне будет превышать атмосферное в 9 раз? Начальное давление в баллоне равно атмосферному.
Данная задача решается так же, как предыдущая, но с одним отличием: в баллоне уже был воздух при атмосферном давлении. Поэтому, записывая уравнение Менделеева-Клапейрона для накаченного воздуха, надо учесть, что создаваемое им давление превышает атмосферное в 8 раз.
Так как по условию задачи компрессор работает так, что ежесекундно засасывает воздух, то число секунд равно числу «засасываний»
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в цилиндр компрессора:
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в баллон:
Поделим второе уравнение на первое:
Время, потребовавшееся для такого накачивания, так же составляет 120с
Задачи на применение газовых законов .
Газовые законы применяют тогда, когда даны два состояния газа и при переходе газа из одного состояния в другое масса газа не меняется.
ГРАФИЧЕСКИЕ ЗАДАЧИ НА ГАЗОВЫЕ ЗАКОНЫ
- На диаграмме РT изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме Р,V .
Проведем поэтапный анализ представленного цикла:
1–2: изохорический процесс; V – const; Р ↑ T ↑
2–3: изотермический процесс; V ↑ Р ↓ Т – const
3–1: изобарический процесс; V ↓ ; Р – const; T ↓
Теперь результаты поэтапного анализа перенесем на диаграмму РV ⇒
- Для постоянной массы идеального газа представлен цикл на диаграмме РV. Изобразить этот цикл на диаграмме VT.
- Изобразите на диаграмме РТ цикл постоянной массы идеального газа, представленный на диаграмме РV.
- Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V 2 > V 1 . Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: Р 1 V 1 = Р 2 V 2 , то Р 1 > Р 2 .
- При нагревании идеального газа постоянной массы получена зависимость Р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры. Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т 2 > Т 1 .
При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V 2 > V 1 . А так как плотность и объем связаны обратной зависимостью (при данной массе), то ρ 1 > ρ 2 , откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
- Как менялась температура постоянной идеального массы газа на протяжении цикла?
Точки 1 и 2 лежат на одной изотерме. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах ⇒
- Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Запишем уравнение Клапейрона–Менделеева:
По условию, T, M и R – постоянные, следовательно, m
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
2–3: T = const, р = const; m
3–4: T = const, V = const; m
4–1: T = const, р = const; m
Аналитические задачи на газовые законы
При решении аналитических задач на газовые законы надо:
- Убедиться, что при изменении состояния масса газа остается постоянной.
- Сделать схематический чертеж, на котором условно отметить состояния газа параметрами Р, V, Т. Записать закон Клапейрона для данных двух состояний.
- Если какой-либо параметр при переходе газа из одного состояния в другое остается неизменным (могут меняться все три параметра), то уравнение Клапейрона перевести в закон Бойля — Мариотта, Гей-Люссака или Шарля.
В случае, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба h, уравнение Клапейрона можно сразу записывать в виде:
- Используя условия задачи, определить термодинамические параметры, выразив их через заданные величины. И если газ граничит с жидкостью, то особое внимание следует обратить на определение давления. Для его определения тех случаях, когда газ производит давление на жидкость, следует использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости.
- Полученную систему уравнений решить относительно неизвестной величины.
- Если в задаче рассматривают состояния нескольких газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно.
- В задачах на газовые законы используется только абсолютная температура.
- При увеличении абсолютной температуры газа в 2 раза давление увеличилось на 25%. во сколько раз изменился объем газа?
Запишем уравнение Клапейрона, так как меняются все три параметра идеального газа:
С учетом данных, уравнение принимает вид:
- Газ изотермически сжат от объема V 1 = 8 л до объема V 2 = 6 л. Давление при этом возросло на Δ Р = 4∙10 3 Па. Определить первоначальное давление.
Запишем уравнение Клапейрона и, так как процесс изотермический, переведем его в закон Бойля-Мариотта
Поэтому можно записать:
Отсюда находим первоначальное давление:
И объемы газов можно оставить в литрах, не переводить в систему СИ.
- При нагревании газа при постоянном давлении на 1К его объем увеличился на 5% от первоначального. При какой температуре находился газ?
- Сколько ртути войдет в стеклянный баллончик объемом V 0 , нагретый до Т 0 , если плотность ртути при температуре Т равна ρ.
- Закрытый с обоих концов цилиндрический сосуд разделен на две равные части теплонепроницаемым поршнем. Длина каждой части 42см. В обеих половинках находится одинаковое количество азота при температуре 27°С и давлении 1 атмосфера. На сколько надо нагреть газ в одной части сосуда, чтобы поршень переместился на 2 см?
Для газа в отделе I:
Для газа в отделе II:
- Объем баллона, содержащего газ под давлением 1,2·10 5 Па составляет 6 литров. Каким станет давление газа, если этот баллон соединить с другим баллоном объем которого 10 литров и он практически не содержит газа.
- Два одинаковых стеклянных шара соединены трубкой. При 0° С капелька ртути находится посередине трубки. Объем воздуха в каждом шаре и части трубки У= 200 см 3 . На какое расстояние х сместится капелька, если один шар нагреть на 2° С, а другой на столько же охладить? Поперечное сечение трубки S=20 мм 2
Для газа в отделе I:
- Температура воздуха в цилиндре 7°С. На сколько переместиться поршень при нагревании воздуха на 20К, если ℓ 1 =14см?
Газ граничит с жидкостью
- Электрическая лампа наполнена азотом при давлении Р= 600 мм рт. ст. Объем лампы V = 500 см 3 . Какая масса воды войдет в лампу, если у нее отломить кончик под водой? Атмосферное давление 760 мм рт. ст.?
Объем воды, поступившей в сосуд равен изменению объема газа при изотермическом процессе. Вода будет заходить в колбу до тех пор, пока давление внутри колбы не станет равным давлению наружному, то есть атмосферному.
Запишем закон Бойля-Мариотта для газа в колбе:%
Отсюда определим изменение объема:
Масса поступившей воды равна:
- Объем пузырька воздуха по мере всплывания со дна озера на поверхность увеличивается в 3 раза. Какова глубина озера?
- Открытую стеклянную трубку длиной ℓ=1м наполовину погружают в ртуть.Затем трубку закрывают пальцем и вынимают из ртути. Какой длины столбик ртути останется в трубке? атмосферное давление нлормальное.
- Узкая вертикальная цилиндрическая трубка длиной L,закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути ρ. Трубка расположена открытым концом вверх. Какова была длина ℓ столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз, из трубки вылилось половина ртути. атмосферное давление Р 0
- В стеклянной трубке, запаянной с одного конца и расположенной горизонтально, находится столбик воздуха длиной 300мм, закрытый столбиком ртути длиной 200мм. На сколько изменится длина воздушного столбика, если трубку расположить открытым концом вверх? Атмосферное давление нормальное.
- Длинная пробирка открытым концом погружена в сосуд с ртутью. При температуре t 1 = 47 °С уровни ртути в пробирке и в сосуде совпадают. Над уровнем ртути остается часть пробирки длины L = 76см. На какую высоту ℓ поднимется ртуть в пробирке, если ее охладить до температуры t 2 = -33 °С? Атмосферное давление Р 0 = 0,1 МПа.
- Посередине откачанной и запаянной с обоих концов горизонтально расположенной трубки длины L = 1 м находится столбик ртути длины h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на расстояние ℓ = 10 см. До какого давления Р была откачана трубка? Плотность ртути ρ= 13,6∙10 3 кг/м 3 .
В обоих концах трубки воздух первоначально занимал объем
где S — площадь поперечного сечения трубки, и имел давление Р.
Когда трубку поставили вертикально, объем воздуха в верхней части трубки стал
а давление стало Р 1 ;
В нижней части трубки объем стал V 2 = S[(L — h)/2 — ℓ], а давление стало равным Р 2
Согласно закону Бойля-Мариотта для верхней части трубки PV = P 1 V 2
Откуда (L — h) P =(L-h + 2ℓ)P 1 ;
Для нижней части трубки
PV = P 2 V 2 , откуда (L-h)P = (L-h-2ℓ)Р 2 .
С другой стороны, столбик ртути находится в равновесии, когда давление воздуха в нижней части трубки равно сумме давлений воздуха в верхней части трубки и столбика ртути, т.е.
Исключив Р 1 иР 2 из уравнений, найдем = 50 кПа.
📽️ Видео
Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать
Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать
Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать
идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать
Физика 10 класс. Газовые законы. Решение задачСкачать
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
Решение графических задач на тему Газовые законыСкачать
Физика. 10 класс. Уравнение состояния идеального газаСкачать
10 класс урок №39 Уравнение состояния идеального газаСкачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Тема 5. Уравнение состояния идеального газа. Давление смеси газов. Решение задач по темеСкачать
Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

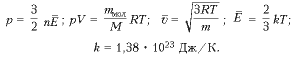
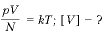
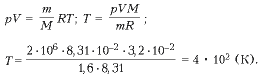
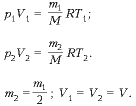
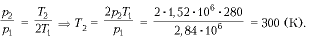
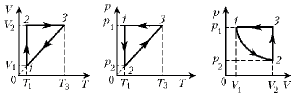
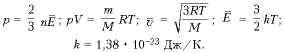
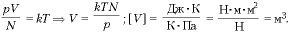

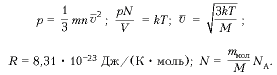
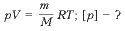
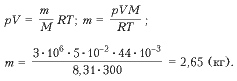
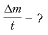
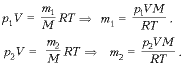
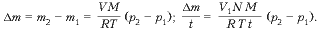
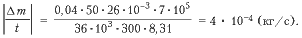
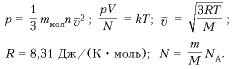

 Выведем размерность искомой физической величины:
Выведем размерность искомой физической величины:


 Отсюда температура
Отсюда температура  кислорода.
кислорода. ( Ответы : m=16 кг ; Р =249300 Па ; V=0,03 м 3; Т =150 К )
( Ответы : m=16 кг ; Р =249300 Па ; V=0,03 м 3; Т =150 К )