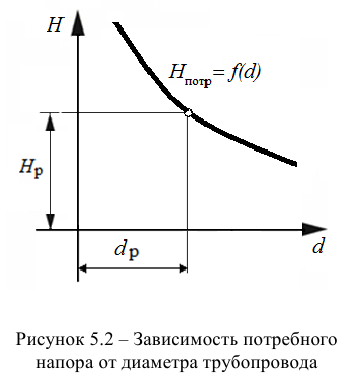
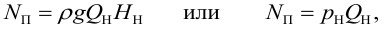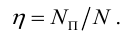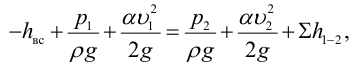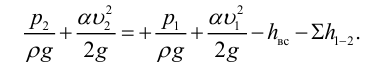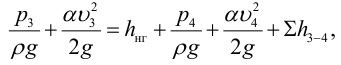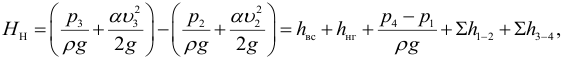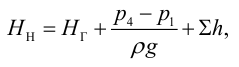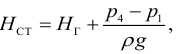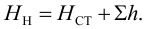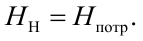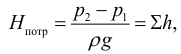Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.
Что такое идеальная жидкость?
Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.
Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
- Гидравлика задачи с решением
- Гидравлика
- Основные физические свойства жидкостей и газов
- Задача №1.2
- Гидростатика
- Указания к решению задач:
- Задача №2.1
- Применение уравнения Бернулли
- Задача №3.1
- Гидравлические сопротивления
- Задача №4.1
- Задачи на гидравлический расчет трубопроводов
- Задача на гидравлический расчет сложного напорного трубопровода
- Задача на расчет трубопровода с насосной подачей жидкости
- Гидравлика с примерами решения задач
- 📸 Видео
Видео:Уравнение Бернулли гидравликаСкачать

Гидравлика задачи с решением
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Гидравлика
Гидравлика — это наука, изучающая законы равновесия и движения жидкостей и газов, в том числе паров жидкости, то есть воды. Если строго следовать научно-техническим канонам, то гидравлика, в отличие от теоретической гидромеханики, управляет сложным и строгим математическим аппаратом («Механика жидкостей и газов»), прежде всего, является технической наукой, главной задачей которой является решение проблем на практике. По этой причине разработка практических методов расчета в гидравлике очень часто предполагает использование различных предположений и допущений, во многих случаях ограничиваясь одномерными потоками в стационарных режимах. Во многих случаях используются результаты экспериментальных данных, которые после соответствующей математической обработки используются в качестве математических уравнений для решения целого ряда аналогичных задач.
Основные физические свойства жидкостей и газов
Указания к решению задач:
Основными физическими характеристиками жидкости являются плотность, вязкость, сжимаемость, температурное расширение, испаряемость. Характеристики определяются с помощью следующих формул:
динамическая вязкость 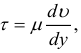
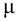
сжимаемость 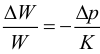
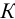
определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С;
испаряемость Жидкости испаряются при любой температуре при наличии свободного объема. Испарение происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10 раз энергию по сравнению со средней. С повышением внешнего давления температура кипения увеличивается, а с понижением (вакуум) — уменьшается. Зависимость давления насыщенного пара от температуры выражается уравнением Клаузиуса-Клапейрона
где 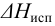
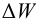
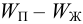
При испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой, поэтому объемом жидкости в уравнении можно пренебречь, тогда
С учетом уравнения Менделеева-Клапейрона
Интегрировав данное выражение получим формулу Клазиуса-Клапейрона
Возможно эта страница вам будет полезна:
Задача №1.2
Определить плотности воды и нефти при 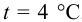
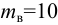
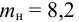
Решение:
плотность воды при заданных условиях:
а плотность нефти:
Видео:Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Гидростатика
Гидростатика — это раздел физики непрерывных сред, изучающий равновесие жидкостей, особенно в области гравитации.
Гидростатика — это теория поведения неподвижных жидкостей. Прежде всего, полезно сравнить гидростатику с теорией упругости, в которой изучается равновесие твердых тел.
Указания к решению задач:
Гидростатика — это раздел гидравлики, изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределение в ней давления. Основные величины, используемые в гидростатике -это давление 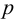
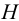
Гидростатическим давлением 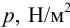
Гидростатическое давление жидкости складывается из давления на ее свободную поверхность 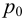
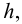
где 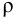
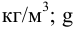
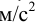
Гидростатическое давление называют абсолютным 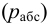
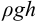
где 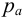
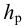
Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного, т.е. разность между атмосферным или барометрическим и абсолютным давлением:
Полная сила, действующая на плоскую стенку 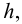
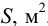
где 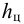
Полная сила, действующая на цилиндрическую поверхность:
где 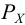
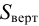
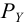
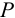
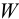
Направление полной силы давления 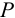
На любое тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом (закон Архимеда):
где 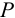
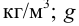
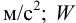
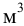
Возможно эта страница вам будет полезна:
Задача №2.1
Определить полное гидростатическое и манометрическое давление на дне сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде 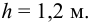
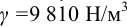
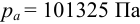
Решение:
1) Определим полное гидростатическое давление в точке:
2) Манометрическое давление на дне сосуда определяется как разность между полным гидростатическим и атмосферным давлениями:
Применение уравнения Бернулли
Основным объектом изучения гидродинамики является поток жидкости. Различают объемный расход 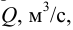
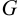
где 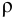
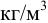
Скорость потока определяется как объемный расход вещества через единицу площади сечения потока, 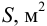
Отсюда следует, что скорости обратно пропорциональны площадям поперечного сечения потоков:
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одно и то же количество жидкости (уравнение неразрывности потока):
Основным уравнением гидравлики, определяющим связь между давлением и скоростью в движущемся потоке идеальной жидкости, является уравнение Берну или, все члены которого имеют размерность длины и измеряются высотой столба жидкости:
где 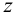
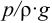
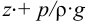
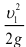
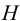
Физически уравнение Бернулли есть математическая запись закона сохранения и превращения энергии применительно к движущейся жидкости. Из уравнения следует, что если на участке потока уменьшается скорость (кинетическая энергия), то на этом участке должно возрастать давление (потенциальная энергия).
Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение примет вид, которым также часто пользуются:
Если же энергию жидкости отнести к единице массы, можно получить 3-ю формулу записи уравнения:
Для потока реальной (вязкой) жидкости уравнение Бернулли запишем в следующем виде:
где 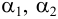
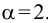
Указания к решению задач:
Часть задач раздела рассчитана на применение уравнения Бернулли для идеальной жидкости, без учета гидравлических потерь. Другая часть задач решается с помощью уравнений Бернулли для потока реальной жидкости.
При применении уравнения Бернулли важно правильно выбрать два сечения, для которых оно записывается.
В качестве сечений рекомендуется выбирать:
- свободную поверхность жидкости в резервуаре
);
- выход в атмосферу
;
- сечение, где установлен манометр, пьезометр или вакуумметр;
- неподвижный воздух на достаточном удалении от трубы всасывания из атмосферы.
Уравнение Бернулли рекомендуется вначале записывать в общем виде, а затем произвести замену его членов заданными параметрами. Члены уравнения Бернулли записываются по потоку жидкости, геометрическая высота 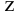
В случае подвода жидкости к резервуару, считается, что теряется вся кинетическая энергия жидкости. Коэффициент Кориолиса « учитывается в случае ламинарного режима.
Возможно эта страница вам будет полезна:
Задача №3.1
Определить расход в водопроводной трубе, если средняя скорость 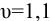
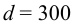
Решение:
Гидравлические сопротивления
Указания к решению задач:
Общие потери напора условно считают равными сумме потерь напора, вызываемых каждым сопротивлением:
где 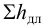
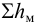
Местные потери определяются по формуле Вейсбаха:
где 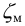
Числовое значение 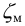
Иногда на него влияет число Рейнольдса. Которое для труб диаметром 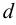
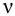
При значениях 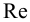
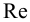
При турбулентном режиме, в случае внезапного расширения потери напора определяются формулой Борда:
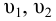
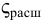
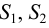
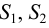
Для других местных сопротивлений коэффициенты находят в справочниках.
Для определения потерь давления на местных сопротивлениях выражение (4.2) приобретает вид:
Потери напора на трение по длине 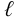
где 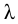
Потери давления на трение по длине находят по следующей формуле
При ламинарном течении
При турбулентном режиме, если
для переходных труб, по формуле Альштуля,
коэффициент 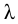
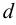

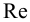
Для гладких труб, по формуле Блазиуса, если
Для гладких труб, по формуле Никурадзе, если
Для области шероховатых труб, по формуле Шифринсона, если
Местные потери в трубах при малых числах Рейнольдса зависят не только от геометрических характеристик сопротивления [1], но и от числа Рейнольдса и могут быть при ориентировочных расчетах найдены по формуле Альтшуля:
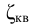
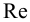
Возможно эта страница вам будет полезна:
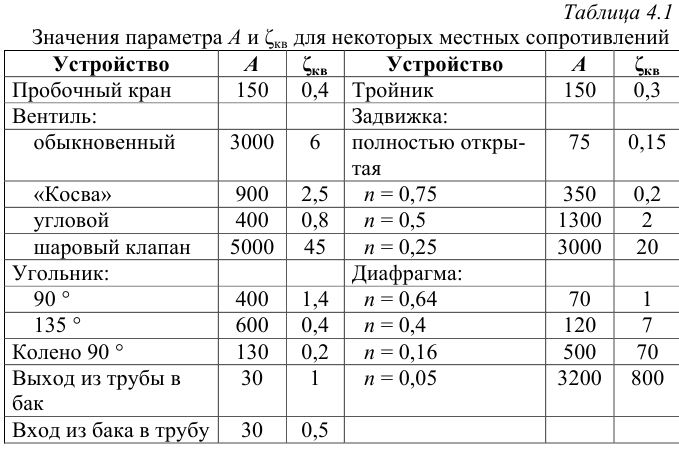
Задача №4.1
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр 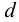
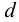
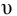
Решение:
Температура воды в системах водоснабжения и канализации изменяется в пределах от 0 °С до 30 °С, кинематические вязкости по таблицам [1] составляют
1) Определим минимальное число Рейнольдса:
2) Определим максимальное число Рейнольдса:
Задачи на гидравлический расчет трубопроводов
Трубопроводы — это система напорных труб, предназначенных для перемещения разнообразных жидкостей и газов [20].
В гидравлике при расчете трубопроводов их подразделяют на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5-10 % потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. Ко вторым относятся трубопроводы, в которых местные потери менее 5-10% потерь напора по длине. Их расчет ведется без учета местных потерь. Длинные трубопроводы можно разделить на простые и сложные.
Простыми трубопроводами называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений.
К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями, кольцевые и т.д.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Запас энергии должен быть создан работой насоса, давлением газа или за счет разности уровней жидкости.
Указания к решению задач:
Основными расчетными формулами для простого напорного трубопровода являются: уравнение Бернулли, уравнение постоянства расход, а также зависимости для определения потерь напора на трение по длине и в местных сопротивлениях [4, 21].
Если в трубопроводе необходимо обеспечить расход жидкости 
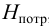
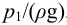
где 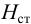
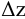
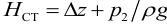
Потери напора выражают через расход 
где 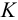
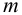
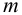
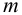
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Для турбулентного режима течения жидкости в квадратичной области, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
Формулы (5.2), дополненная выражениями (5.3) и (5.4), является основной для расчета простых трубопроводов [4, 21].
Если трубопровод лежит в горизонтальной плоскости, а противодавление 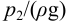
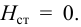
Выражение (5.5) называется гидравлической характеристикой трубопровода, которая показывает зависимость суммарной потери напора (или давления) в трубопроводе от расхода.
При ламинарном режиме течения гидравлическая характеристика представляет собой прямую линию, а при турбулентном в квадратичной области — параболу второй степени [20].
Задачи по расчету простого трубопровода можно разбить на три типа:
Тип 1. Известны: расход жидкости 
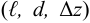
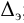
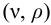
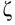
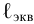
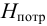
По известным значениям 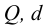
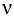
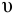
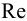
При ламинарном режиме искомый напор находится по формулам (5.2) и (5.3).
При турбулентном режиме задача решается с помощью формул (5.2) и (5.4). Определение зоны сопротивления производится с помощью формул Блазиуса или Альтшуля, в зависимости от шероховатости труб.
Тип 2. Известны: напор в начальном сечении (располагаемый напор 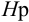

Расчет начинается с предположения о режиме течения жидкости. Так при течении маловязких жидкостей (воды, бензина, керосина и т.п.) целесообразно принимать режим течения турбулентным, при течении вязких жидкостей (масла, нефти и т.п.) — ламинарный.
При ламинарном режиме течения задача решается с помощью формул (5.2) и (5.3).
При турбулентном режиме в уравнениях (5.2) и (5.4) содержатся две неизвестные 
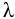
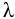
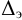
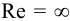
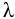
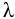
Вторым вариантом решения задачи является графоаналитический метод. Для этого необходимо построить гидравлическую характеристику трубопровода 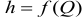
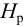

Гидравлическая характеристика трубопровода строится по данным расчета потерь напора при различных величинах расхода, т.е. решения задачи 1-го типа.
По известной величине напора 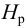
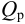
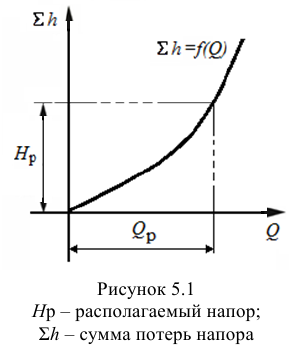
Тип 3. Известны следующие данные: расход жидкости 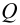
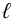
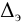
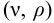
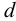
Задачу рекомендуется решать графоаналитическим способом (рис. 5.2), путем построения кривой взаимосвязи между потребным напором 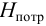
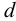
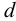
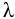
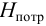
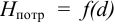
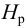
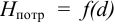
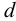
В конечном итоге принимается ближайший стандартный диаметр.
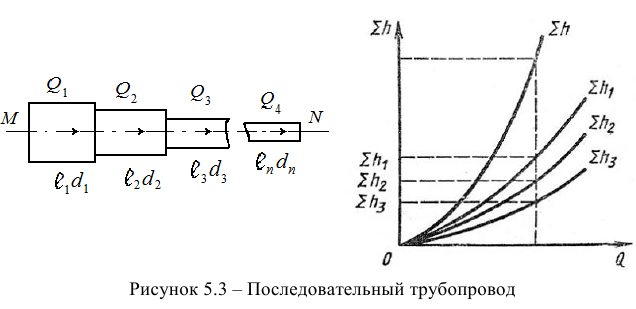
Расчет последовательно соединенного трубопровода
Последовательным называется такое соединение трубопроводов, при котором жидкость протекает по простым трубопроводам разного диаметра, последовательно соединенных в одну нитку (рис. 5.3). По всем участкам трубопровода протекает одинаковый расход жидкости 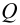
Потери напора в таком трубопроводе равны сумме всех местных потерь и потерь по длине:
где 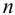
Если известны характеристики каждого участка трубопровода, то по ним можно построить характеристику всего последовательного соединения 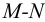
Возможно эта страница вам будет полезна:
Задача на гидравлический расчет сложного напорного трубопровода
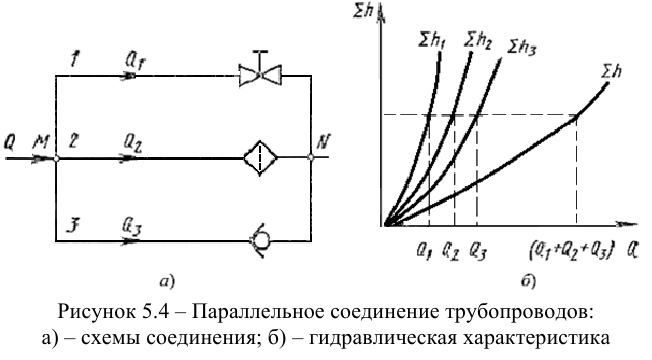
Сложный трубопровод обычно состоит из простых трубопроводов, которые соединены параллельно, либо имеет разветвления. Параллельным называется соединение трубопроводов, при котором жидкость, подходя к точке разветвления, течет по ответвлениям и далее снова сливается в один трубопровод, т.е. параллельно соединенные трубопроводы имеют общую точку разветвления и общий узел соединения (рис. 5.4).
Расход жидкости в основной магистрали равен сумме расходов в параллельных трубопроводах, а потери напора равны между собой:
где 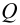
Потери напора можно выразить через соответствующие расходы:
где 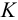
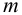
Для построения характеристики параллельного соединения нескольких трубопроводов следует сложить расходы характеристик этих трубопроводов при одинаковых ординатах (рис. 5.4, б).
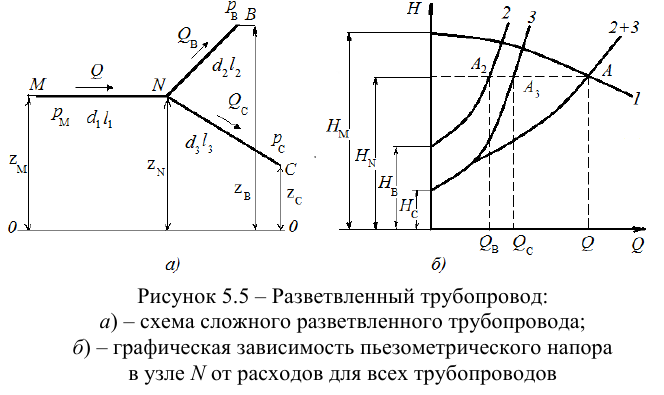
Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб (рис. 5.5).
Алгоритм расчета разветвленного трубопровода включает следующие действия:
1) разбить сложный трубопровод на ряд простых;
2) рассчитать и построить кривые потребных напоров для каждого из простых трубопроводов;
3) провести графическое сложение параллельных участков;
4) провести графическое сложение последовательных участков.
ВНИМАНИЕ: при расчете разветвленного трубопровода необходимо идти от конечных точек к его начальной точке, т.е. против течения.
Приведем расчет разветвленного трубопровода (рис. 5.5). Трубопровод 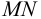
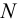
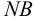
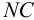
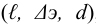
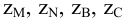
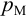
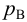
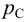
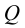
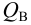
Величины пьезометрических напоров в точках 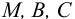
Для решения задачи составим систему уравнений, связывающих искомые расходы 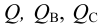
Представим три верхних уравнения системы (5.9), в виде системы уравнений пьезометрических напоров для трубопроводов 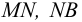
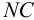
По уравнениям (5.10) строятся графические зависимости пьезометрического напора в узле 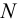
Зависимость суммарного расхода (уравнение 4 в системе (5.9)) в трубопроводах 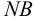
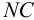
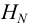
Значение напора 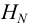
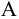
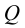
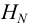
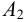
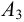
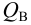
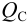
Теория из учебников и готовые задачи на продажу тут.
Задача на расчет трубопровода с насосной подачей жидкости
Основными понятиями для расчета таких трубопроводов являют-
- объемная подача насоса (подача
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
;
- напором насоса
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
- мощность насоса (потребляемая)
— это энергия, подводимая к насосу от двигателя за единицу времени, Вт;
- мощность насоса (полезная)
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
полезную мощность можно выразить:
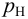
Мощность насоса 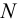
- характеристика насоса — графическое изображение зависимостей напора насоса
(или давления
), мощности
и КПД от подачи насоса
при постоянной частоте вращения;
- разомкнутый трубопровод с насосной подачей — это трубопровод, по которому жидкость перекачивается из одного места в другое;
- замкнутый (кольцевой) трубопровод с насосной подачей — это трубопровод, в котором циркулирует одно и тоже количество жидкости.
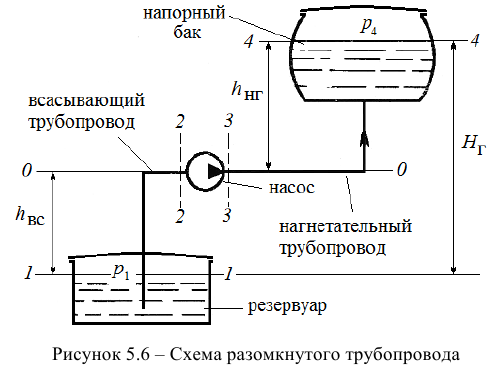
Рассмотрим решение задачи по расчету потребного напора разомкнутого трубопровода и построению на одном графике рабочей характеристики насоса и характеристики насосной установки.
Точка пересечения этих характеристик называется рабочей точкой.
1) Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса (рис. 5.6):
где 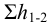
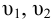
Удельная энергия перед входом в насос составит:
2) Запишем уравнение Бернулли для потока жидкости в нагнетательном трубопроводе для сечений 3-3 и 4-4 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса:
где 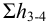
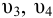
Так как скоростные напоры жидкости в баках 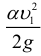
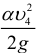
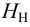
где 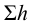
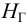
Обозначив через статический напор 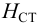
получим следующее выражение:
Таким образом, при установившемся режиме работы насоса его напор 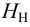
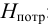
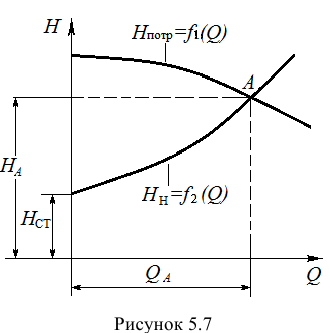
На полученном равенстве основан метод расчета трубопроводов, питаемых насосом, который заключается в построении на одном графике рабочей характеристики насоса 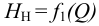
Точка пересечения этих характеристик называется рабочей точкой, в которой справедливо равенство (5.19).
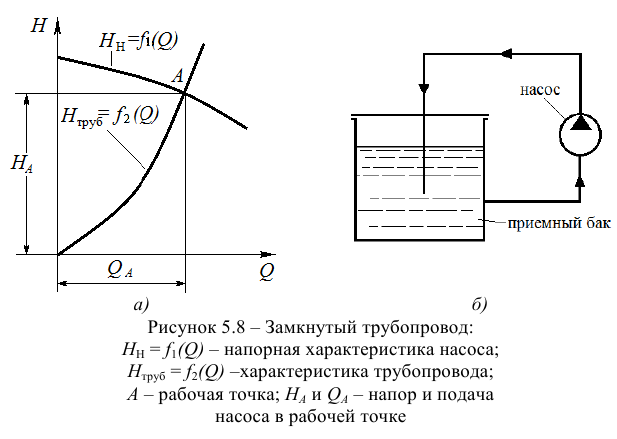
В случае замкнутого трубопровода (рис. 5.8) геометрическая высота подъема жидкости равна нулю (геометрический напор 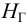
Следовательно, при значениях 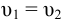
то есть, между потребным напором и напором, развиваемым насосом выполняется равенство (5.19).
Эти страницы вам могут пригодиться:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Закон БернуллиСкачать

Гидравлика с примерами решения задач
- Александра Стаханова 5 лет назад Просмотров:
1 Федеральное агентство по образованию псковский государственный политехнический институт О. В. Ворожцов Гидравлика с примерами решения задач Учебно методическое пособие для студентов специальности Эксплуатация наземного транспорта и транспортного оборудования Псков
2 Оглавление Введение 5 Раздел 1. Жидкости и их физические свойства Жидкости. Гипотеза сплошности. Силы, действующие в жидкости Плотность жидкости Физические свойства жидкостей Примеры решения задач.19 Раздел 2. Гидростатика Гидростатическое давление и его свойства Основное уравнение гидростатики Геометрическая интерпретация основного уравнения гидростатики. Избыточное, вакуумметрическое и абсолютное давление. Измерение давления Относительный покой. Равновесие жидкости в движущемся сосуде Примеры решения задач.32 Раздел 3. Кинематика жидкости Основные понятия и определения Расход. Уравнение расхода Потоки жидкости Примеры решения задач.45 Раздел 4. Динамика жидкости Уравнение Бернулли для элементарной струйки идеальной жидкости Энергетическая интерпретация уравнения Бернулли для установившегося движения Уравнение Бернулли для потока реальной жидкости Измерение расходов и скоростей жидкости Примеры решения задач.59 Раздел 5. Режимы движения жидкости. Уравнение Рейнольдса Основы гидродинамического подобия Режимы течения жидкости Ламинарный режим Течение жидкости в узких (капиллярных) щелях Турбулентный режим Примеры решения задач.78 4
3 Раздел 6. Потери напора (удельной энергии) Общие сведения о гидравлических сопротивлениях Местные сопротивления Потери напора по длине потока Примеры решения задач.87 Раздел 7. Истечение жидкости Истечение через отверстие в тонкой стенке при постоянном напоре Истечение под уровень Примеры решения задач.97 Раздел 8. Гидравлический расчет трубопроводов Классификация трубопроводов Расчет простых трубопроводов Соединения простых трубопроводов Трубопровод с насосной подачей Примеры решения задач Раздел 9. Основы гидропневмопривода Общие сведения Гидравлический привод Пневматический привод Контрольные вопросы Приложение..134 Список литературы
4 Введение Гидравлика это наука, изучающая законы равновесия и движения жидкостей, а также законы взаимодействия жидкостей с окружающими их граничными поверхностями и с твердыми или упругими телами, погруженными (частично или полностью) в жидкость. Название «гидравлика» произошло от греческих слов «хюдор» — вода и «аулос» — труба, желоб. В настоящее время почти во всех областях техники применяют различные гидравлические устройства, основанные на использовании гидравлических законов. Главнейшие области применения гидравлики гидротехника, мелиорация и водное хозяйство, гидроэнергетика, водоснабжение и канализация, водный транспорт, машиностроение, авиация и т. д. При исследовании гидравлических явлений в гидравлике применяют теоретический и экспериментальный методы. В теоретическом методе используют уравнения механики для математического описания практически всех процессов, происходящих в движущейся жидкости. Ввиду сложности строения жидкостей теоретические исследования проводят для модельных жидкостей, что облегчает применение уравнений механики. Например, применяют модель невязкой жидкости, которая в отличие от существующих в природе реальных жидкостей лишена свойства вязкости. Этот метод привел к созданию теоретической гидромеханики, имеющий строго математический характер. Однако использование этих математических моделей не всегда позволяет решать практические задачи. Это связано, с одной стороны, со сложностью используемых математических зависимостей, а с другой стороны с необходимостью учета влияния большого числа конструктивных факторов. Экспериментальные исследования в гидравлике имеют важное значение. Леонардо да Винчи ( г.г.), написавшему работу «О движении и измерении воды», которая была опубликована спустя более чем 400 лет после его смерти, принадлежат слова: «Всякий раз, когда имеешь дело с водой, прежде всего обратись к опыту, а потом уже рассуждай». Изучение гидравлических явлений на моделях, созданных на основе теории подобия с применением определенных методик моделирования, позволяет получить данные о параметрах, которыми будет характеризоваться явление в реальных условиях. Оптимальное сочетание теоретических и экспериментальных исследований позволяет получить результат, достаточно точно описывающий исследуемое явление. 6
5 Раздел 1 Жидкости и их физические свойства 1.1. Жидкости. Гипотеза сплошности. Силы, действующие в жидкости. Жидкости. Все вещества в природе имеют молекулярное строение. По характеру молекулярных движений, а также по числовым значениям межмолекулярных сил жидкости занимают промежуточное положение между газами и твердыми телами. Молекулы жидкости находятся в непрерывном хаотичном тепловом движении, осуществляющемся в виде колебаний (10 13 колебаний в секунду) относительно мгновенных центров и скачкообразных переходов от одного центра к другому. Тепловое движение молекул твердых тел колебания относительно стабильных центров, тепловое движение молекул газа непрерывные скачкообразные перемены мест. Жидкими телами или жидкостями называют физические тела, легко изменяющие свою форму под действием самой незначительной по величине силы. Можно сказать, что жидкость это физическое тело, обладающее текучестью, имеющее определенный объем и заполняющая часть пространства (сосуда), равного ее объему. Различают два вида жидкостей: -жидкости капельные (малосжимаемые); -жидкости газообразные (сжимаемые). Газообразные жидкости (газы) в отличие от жидкостей капельных заполняют все предоставленное им пространство и изменяют свой объем в зависимости от изменения температуры и давления. Газообразные жидкости, их свойства и применение рассматриваются в специальных дисциплинах термодинамике и аэромеханике. В гидравлике рассматривается равновесие и движение капельной жидкости, в дальнейшем называемое просто жидкостью. Капельные жидкости представляют собой жидкости в обычном, общепринятом понимании этого слова (вода, нефть, керосин и т. д.) Гипотеза сплошности. В гидравлике жидкость рассматривают как деформируемую систему материальных точек (частиц), непрерывно заполняющих пространство, в котором она движется. Предполагают, что частица жидкости представляет собой бесконечно малый объем, в котором находится достаточно много молекул жидкости. Например, в кубике воды со сторонами размером 0,01 мм будет находиться 3, молекул. 7
6 При таком предположении жидкость в целом рассматривают как сплошную среду (континуум), непрерывно заполняющую пространство, т. е. принимают, что в жидкости нет пустот или разрывов. Ввиду большого количества молекул, составляющих частицу жидкости, влияние отдельных молекул не учитывается. Сплошная среда представляет собой модель, которую успешно используют при исследовании закономерностей покоя и движения жидкости. Силы, действующие в жидкости. Вследствие текучести жидкости она не воспринимает сосредоточенные силы, поэтому в жидкости действуют только распределенные по объему или по поверхности силы. Поэтому силы, действующие на жидкость, принято делить на массовые (объемные) и поверхностные. Массовые (объемные) силы это силы, действующие на каждую частицу жидкости с массой m, то есть это силы, распределенные по массе. К ним относятся: сила тяжести, сила инерции (кариолисова сила инерции, переносная сила инерции), гравитационные силы. Поверхностные силы это силы, действующие на каждый элемент поверхностей S, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости. Пусть на плоскую поверхность площадью S действует сила R (рис. 1.1). Силу R можно разложить на нормальную р и тангенциальную Т составляющие. Рис Схема действия поверхностных сил Тангенциальная составляющая Т называется силой трения и вызывает в жидкости касательные напряжения. Среднее напряжение трения τ, действующее касательно к площади S, будет равно: τ ср = Т S. 8
7 Среднее касательное напряжение не дает точного значения касательного напряжения в любой точке площади S. Поэтому касательное напряжение в данной точке равно пределу, к которому стремится отношение силы трения Т к площади S, касательно к которой она действует, при уменьшении S до нуля, т. е. при стягивании ее к размерам точки: τ = lim S. (1.1) Выражение (1.1) можно назвать плотностью распределения касательных сил (сил трения) по площади S. Единицей измерения касательных напряжений в системе СИ является паскаль (Па) ньютон, отнесенный к квадратному метру (1 Па = 1 Н/м 2 ). Нормальная сила р называется силой давления и вызывает в жидкости нормальные напряжения сжатия. Если сила давления р равномерно распределена по площадке S, то среднее (единичное) давление будет равно: р ср = S. Плотность распределения нормальных сил: р = lim S. (1.2) За единицу давления в системе СИ принят паскаль (1 Па = 1 Н/м 2 ). Раньше давление измерялось в кгс/см 2 (1 кгс/см 2 = 1 атмосфера). Поскольку при применении единицы «паскаль» получаются большие цифровые значения, ее заменяют на бары: 1 бар = Па. Итак, соотношения между различными единицами измерения давления следующие: 1 кгс/см 2 = 1 ат = 1 бар = 0.1 МПа Плотность жидкости. Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют «весомость» жидкости. Плотность ρ характеризует распределение массы m жидкости по объему W. В произвольной т.а жидкости плотность распределения массы равна: р а = lim m W, где m масса, заключенная в объеме W, стягиваемом в точку а. 9
8 Плотность однородной жидкости равна отношению массы m жидкости к ее объему: ρ = m W. (1.3) Плотность ρ во всех точках однородной жидкости одинакова. В общем случае плотность может изменяться в объеме жидкости от точки к точке и в каждой точке объема с течением времени. За единицу плотности в системе СИ принят 1 кг/м 3. Вместо плотности в формулах может быть использован также удельный вес γ (Н/м 3 ), то есть вес жидкости G, приходящийся на единицу объема W: γ = G W = mg W = ρg. (1.4) Плотность жидкостей и газов зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с увеличением температуры. Плотность воды максимальна при t =4 ºС и уменьшается как с уменьшением, так и с увеличением температуры от этого значения. В этом проявляется одно из аномальных свойств воды. Плотность воды при t =4º С составляет 1000 кг/м 3 ; морской воды кг/м 3 ; нефти и нефтепродуктов кг/м 3 ; чистой ртути кг/м 3 ; воздуха при t =0º С и атмосферном давлении 1,29 кг/м 3. При изменении давления плотность жидкости изменяется незначительно Физические свойства жидкостей. Сжимаемость. Это свойство жидкостей изменять объем при изменении давления; характеризуется коэффициентом объемного сжатия (коэффициентом сжимаемости) β р (Па -1 ); представляющим собой относительное изменение объема жидкости W при изменении давления на единицу: β р =, (1.5) где W первоначальный объем жидкости; dw относительное изменение объема жидкости при изменении давления на величину dр. Знак » » в формуле (1.5) указывает на то, что при увеличении давления объем жидкости уменьшается. На рис. (1.2) можно видеть зависимость сжимаемости жидкости от ее химической природы. 10
9 Рис.1.2. Зависимость сжимаемости различных жидкостей от давления: 1 глицерин; 2 вода; 3 масло; 4 силиконовая рабочая жидкость Изменение плотности при изменении давления учитывается формулой (1.6): ρ ρ 1 β р d, (1.6) где ρ и ρ 1 плотность жидкости при давлении р и р 1 соответственно; dр перепад давлений (dр = р р 1 ). Величина, обратная коэффициенту объемного сжатия модуль объемной упругости жидкости Е о, (Па): Е о = 1 β р. (1.7) Физический смысл объемного модуля упругости можно представить, если считать, что W = 1 м 3, а dр = 1 Па. Тогда Е о = 1 dw, то есть модуль упругости можно представить как величину, обратную изменению объема одного кубического метра жидкости при изменении давления на одну единицу. Объемный модуль упругости жидкости зависит от типа жидкости, давления и температуры. Однако в большинстве случаев Е о считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур и давлений. Различают изотермический и адиабатический модуль упругости. Причем для расчетов обычно используют изотермический модуль упругости Е то, применяемый для анализа медленных процессов, при которых успевает завершиться теплообмен с окружающей средой. Для быстротечных процессов, при которых теплообмен не успевает завершиться, используют адиабатический модуль упругости Е ао. 11
10 Сжимаемость жидкостей очень незначительна, и в большинстве случаев ее можно считать несжимаемой. Однако, если бы вода в Мировом океане (средняя глубина 3704 м) была несжимаемой, ее уровень повысился бы на 27 м. Объем легкого минерального масла, применяемого в жидкостных амортизаторах шасси самолетов при нормальной температуре, уменьшается при повышении давления от 0 до 35 МПа на 1,7 %, а керосина на 0,8 %. Сжимаемость рабочих жидкостей приводит к понижению жесткости гидравлической системы, а следовательно, к потере передаваемой мощности. Температурное расширение. Это свойство жидкостей изменять объем при изменении температуры; характеризуется температурным коэффициентом объемного расширения β t (1/ С), представляющим собой относительное изменение объема жидкости при изменении температуры на единицу (1 ºС) и при постоянном давлении: β t =, (1.8) где W первоначальный объем жидкости; dw относительное изменение объема жидкости при повышении температуры на dt. Для большинства жидкостей коэффициент β t с увеличением давления уменьшается (рис. 1.3). Рис Зависимость коэффициента объемного расширения β t от давления р Для воды с увеличением давления при температуре до 50 ºС коэффициент β t растет, а при температуре выше 50 ºС уменьшается. В общем случае для капельных жидкостей значение β t невелико, и обычно при расчетах не учитывается. Однако в ряде случаев при больших перепадах температуры изменение плотности жидкости приходиться учитывать: 12
11 ρ ρ 1+ β t, (1.9) где ρ и ρ 1 плотности при температурах t и t 1 ( t = t t 1 ). Вязкость. Это свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения или силами вязкости. Благодаря этим силам слой жидкости, движущийся медленнее, «тормозит» соседний слой, движущийся быстрее. Силы внутреннего трения проявляются вследствие наличия межмолекулярных связей между движущимися слоями. Силы внутреннего трения в жидкости впервые были обнаружены Ньютоном в 1686 г., а затем экспериментально обоснованы проф. Н. П. Петровым в 1883 г. Для выяснения физической сущности понятия вязкости рассмотрим следующую схему (рис. 1.4). Рис Схема течения жидкости между двумя пластинами Пусть имеются две параллельные пластины А и В, в пространстве между которыми заключена жидкость; нижняя пластина А неподвижна, верхняя пластина В движется поступательно с некоторой постоянной скоростью υ. Слои жидкости, непосредственно прилегающие к пластинам («прилипшие» слои), будут иметь одинаковые с ними скорости, т. е. слой, прилегающий к верхней пластине В, будет двигаться со скоростью υ, а слой, прилегающий к нижней пластине А, будет находиться в покое. Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластины. 13
12 Если расстояние между пластинами обозначить через n, то скорость υ y слоя жидкости, находящегося на расстоянии y от этой пластины, будет равна: υ y = υ. Ньютоном было высказано предположение, впоследствии подтвержденное опытом, что силы сопротивления, возникающие при таком скольжении, пропорциональны площади соприкосновения слоев и скорости скольжения. Принимая площадь соприкосновения равной единице, получим: τ = μ, (1.10) где τ сила сопротивления, отнесенная к единице площади (касательное напряжение), μ коэффициент пропорциональности, учитывающий особенности конкретных жидкостей и называемый коэффициентом динамической вязкости жидкости, dυ/dy градиент скорости (скорость деформации сдвига), то есть величина изменения скорости в направлении, нормальном к направлению вектора самой скорости. В данном случае dυ/dy = υ/n. При слоистом прямолинейном течении жидкости в цилиндрической трубе круглого поперечного сечения жидкость движется кольцевыми цилиндрическими слоями толщиной dy, скорость слоев уменьшается от оси к стенкам трубы и максимальна в центре по оси трубы (рис. 1.5.). Рис. 1.5 Схема движения жидкости в цилиндрической трубе Разность скоростей в соседних слоях равна dυ (рис. 1.6). Касательное напряжение в данном случае согласно формуле (1.10) равно: τ = ±μ. (1.11) Знак «+» или «-» указывает направление отсчета расстояний (от стенки рассматриваемой трубы или от ее оси). Градиент скорости мо- 14
13 жет быть положительным, если расстояние отсчитывается от стенки трубы, или отрицательным (от ее оси). Рис Профиль скоростей при течении вязкой жидкости вдоль стенки Напряжения трения возможны лишь в движущейся жидкости, т.е. вязкость жидкости проявляется лишь при ее течении. Жидкости, для которых справедлив закон внутреннего трения Ньютона, называются ньютоновскими. Существуют жидкости (коллоидные суспензии, растворы полимеров, гидросмеси из глины, цемента, строительные растворы и т.п.), для которых связь между касательным напряжением τ и скоростью сдвиговой деформации dυ/dy будет выражаться соотношением: τ = τ о + μ. (1.12) Рис Зависимость между касательным напряжением для обычных (1) жидкостей и вязкопластичных (2) Такие жидкости относятся к неньютоновским и называются вязкопластичными или аномальными. Опытами установлено, что в подобных жидкостях движение наступает только после того, как касательные напряжения достигнут некоторого предельного минимального значения, обычно называемого начальным напряжением сдвига. 15
14 Таким образом, вязкопластичные жидкости отличаются от ньютоновских наличием касательного напряжения в состоянии покоя τ о. В память французского ученого Пуазейля единица вязкости была названа «пуаз» с). В системе СИ единицей динамической вязкости является Па с = с = 10 П. В гидравлических расчетах кроме динамической вязкости используют понятие кинематической вязкости, равное отношению динамической вязкости μ к плотности жидкости ρ: ν =. (1.13) Единицей кинематической вязкости в системе СИ принята единица см 2 /с, названная в честь английского ученого Стокса «стокс»; 1 м 2 /с = 10 4 Ст. Сотая доля стокса называется сантистоксом (сст). Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 1.8). Рис Зависимость кинематической вязкости от температуры Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает. Исключением является вода, для которой при температуре до 32 ºС с увеличением давления вязкость уменьшается. С целью облегчить и упростить ряд теоретических выводов и исследований в гидравлике существует понятие «идеальная» жидкость. Ее считают абсолютно несжимаемой, она обладает полным отсутствием температурного расширения и не оказывает сопротивления сдвигающим и растягивающим усилиям. Идеальная жидкость жидкость фиктивная. Но сжимаемость, температурное расширение и сопротивление растяжению для реальных жидкостей ничтожно малы и обычно не учитываются. Таким образом, основной и единственной особенностью, отличающую реальную жидкость от идеальной, является наличие у реальной жидкости сил сопротивления сдвигу, опреде- 16
15 ляемых особым свойством жидкости вязкостью. Поэтому идеальную жидкость иногда называют невязкой, а реальную — вязкой жидкостью. Вязкость жидкостей измеряют при помощи вискозиметров. В различных странах для определения вязкости используют вискозиметры Энглера (в Европе), Сейболта (в США), Редвуда (в Великобритании). Существуют автоматические системы измерения кинематической и динамической вязкости. Растворение газов. Все жидкости в той или иной мере поглощают и растворяют газы. Относительное количество газа, которое может раствориться в жидкости до ее насыщения, прямо пропорционально давлению на поверхности раздела. Объем растворенного газа вычисляется по формуле: W г = k г W ж, (1.14) где W г объем растворенного газа, отнесенный к нормальным условиям (p o, t o ); W ж — объем жидкости; p — давление жидкости; p o — эталонное давление (например, атмосферное); k г — коэффициент растворимости газа в жидкости (объем газа, растворяющегося при атмосферном давлении в единице объема жидкости). Растворимость воздуха в реальной жидкости до ее насыщения зависит от ее вида и плотности. Предельное значение коэффициента растворимости k г могут достигать 0,12-0,2.При температуре 20 ºС и атмосферном давлении в воде содержится 1,6% растворенного воздуха по объему. При повышении температуры коэффициент растворимости уменьшается. При понижении давления растворенный газ выделяется, ухудшая характеристики работы гидравлических систем. Это может произойти, например, в результате внезапного расширения потока жидкости или вследствие больших местных скоростей. Нарушение сплошности движущейся жидкости вследствие местного понижения давления ниже критического называется кавитацией (от латинского «кавитас» — полость). В гидроприводе пузырьки, перемещаясь с потоком жидкости, попадают в область с высоким давлением или низкой температурой и мгновенно смыкаются. В этот момент пар конденсируется и газы снова растворяются в жидкости. В образовавшиеся пустоты с большими скоростями устремляются частицы жидкости, что приводит к местным гидравлическим ударам (резкому и значительному повышению давления в этих местах) и звуковым импульсам. Кавитация в обычных случаях является нежелательным явлением и приводит к: — уменьшению КПД гидромашины; — кавитационной коррозии металла; 17
16 — уменьшению пропускной способности трубопровода; — повышению температуры жидкости; — термоокислению жидкости (воспламенение паров и сгорание частиц жидкости в среде воздушного пузырька эффект Дизеля, что приводит к образованию в жидкости нерастворимых коксообразующих продуктов). Испарение. Это свойство капельной жидкости изменять свое агрегатное состояние, в частности превращаться в пар. Интенсивность испарения (парообразования), происходящего на свободной поверхности жидкости, зависит от рода самой жидкости и условий, в которых она находится. Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении чем выше температура кипения, тем меньше испаряемость. Кипение это процесс перехода жидкости в газообразное состояние, происходящий внутри жидкости. Температура кипения с повышением давления на ее поверхности увеличивается. Если испарение происходит в свободном пространстве, то почти все молекулы, перешедшие при испарении в паровую фазу, удаляются с поверхности жидкости и обратно не возвращаются. Если жидкость находится в замкнутом пространстве, то после достижения в нем определенной концентрации паров устанавливается равновесие между процессами испарения и конденсации, и давление пара становится постоянным. Такой пар, находящийся в замкнутом пространстве в термодинамическом равновесии с жидкостью (число молекул, вырывающихся в единицу времени из жидкости и переходящих в паровую фазу, равно числу молекул, возвращающихся в жидкость за то же время), называют насыщенным. А его давление давлением насыщенного пара при данной температуре. Рис Зависимость давления насыщенных паров от температуры 18
17 На рис приведена зависимость давления насыщенных паров р н.п. воды от температуры. Точка А соответствует температуре 100 ºС и нормальному атмосферному давлению. При повышении давления на свободной поверхности жидкости до значения р 1 температура кипения воды повысится до некоторого значения t. При понижении давления температура кипения понизится. Обычно при понижении давления до давления насыщенных паров жидкости (при данной температуре) в жидкости образуются пузырьки газа, выделившегося из жидкости, т.е. происходит так называемое «холодное кипение». Если парообразование происходит в закрытом сосуде, то оно сопровождается повышением давления. Процесс идет по линии от точки С к точке А, затем В и далее (рис.1.9.), что может привести к разрушению сосуда. Поверхностное натяжение. Является специфическим свойством жидкостей и связано с ее молекулярной структурой. В результате притяжения между молекулами жидкости возникают силы сцепления. Внутри жидкости эти силы уравновешиваются, однако находящиеся на границе раздела поверхности жидкости с газом, твердым телом или двумя несмешиваемыми жидкостями молекулы жидкости испытывают неуравновешенное извне воздействие (отсутствие притяжения со стороны молекул газа). Поэтому появляется сила, направленная внутрь объема жидкости, называемая силой молекулярного давления. Эта сила стремится придать объему жидкости форму с наименьшей поверхностью. Чтобы увеличить поверхность жидкости, необходимо часть внутренних молекул вывести на поверхность, для чего придется совершить работу. Это можно представить как наличие сопротивления граничной поверхности жидкости растяжению и считать, что по поверхности распределены силы, препятствующие растяжению. Эти силы действуют по касательным к поверхности жидкости направлениям и называются силами поверхностного натяжения. Поверхностное натяжение σ (Н/м) представляет собой удельную, отнесенную к единице площади, свободную поверхностную энергию, которой обладают молекулы поверхностного слоя. У большинства жидкостей при 20 ºС σ = 0,01 0,1 Н/м. В трубках малого диаметра (капиллярах) наблюдается искривление свободной поверхности жидкости, граничащей с газом. Если поверхность трубки смачивается, то свободная поверхность жидкости в трубке вогнутая. Если нет смачивания, то свободная поверхность выпуклая. В этих случаях силы поверхностного натяжения обуславливают дополнительное напряжение в жидкости. 19
18 Под действием этих напряжений в трубках малого диаметра происходит капиллярное поднятие (при смачивании) или опускание (если смачивания нет) жидкости на некоторую высоту. Чем меньше диаметр, тем выше или ниже уровень жидкости. Силы поверхностного натяжения приходится учитывать при движении жидкости в трубках малого диаметра (капиллярных трубках) некоторых измерительных приборов. При обычных гидравлических расчетах влиянием этих сил ввиду их малости пренебрегают. Поднятие воды в капиллярах почвы и грунта — важный фактор распространения воды. Высота капиллярного поднятия воды в грунтах изменяется от нуля почти до 5 м (в глинистых почвах) Примеры решения задач Сосуд заполнен водой, занимающей объем W 1 = 2 м 3. На сколько уменьшится и чему будет равен этот объем при увеличении давления на величину на величину 200 бар при температуре 20 ºС? Модуль объемной упругости для воды при данной температуре Е о = 2110 МПа. Изменение объема жидкости определим из уравнения (1.5): W = β p W p. Коэффициент объемного сжатия определим из уравнения (1.7): β p = 1 Е = = 4, /Па. Увеличение давления р = 200 бар = Па. Тогда: W = 4, = 0,019 м 3. Искомый объем будет равен: W 2 = W 1 W = 1,981 м Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 ºС. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 ºС. Модуль объемной упругости бензина принять равным Е о =1300 МПа, коэффициент температурного расширения β t = /град. Из уравнения (1.8) находим относительное изменение объема бензина при увеличении температуры t на 30 ºС ( t = t 2 t 1 = 30 ºС): W W = β t t = = 0,024. Из уравнения (1.5) находим изменение давления р при увеличении температуры t на 30 ºС: 20
19 р = р = Е о = 0, = 31,2 МПа Плотность масла АМГ-10 при температуре 20 ºС составляет 850 кг/м 3. Определить плотность масла при повышении температуры до 60 ºС и увеличении давления с атмосферного (р 1 =0,1 МПа) до р 2 =8,7 МПа. Модуль объемной упругости масла Е о =1305 МПа, температурный коэффициент β t = 0,0008 1/град. Плотность масла при повышении температуры до значения t 2 = 60 ºС вычислим по формуле (1.9): ρ I = ρ 1+ β t = ,0008 (60 20) = 823,6 кг/м3. Плотность масла при повышении давления до значения p 2 = 8,7 МПа вычисляем по формулам (1.6) и (1.7): ρ II = ρ 1 β р d = I, ( ) = = 829 кг/м 3., Е Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние h = 5 мм. Начальная высота положения поршня (без груза) H = 1,5 м; диаметр поршня d = 80 мм и резервуара D = 300 мм; высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким. — Сила тяжести, создаваема грузом А, будет равна: F = mg = 2450 Н. Давление, создаваемое этой силой (т.е. приращение давления dр), определим как: 21
20 dр = F S = 4F = п πd = 490 кпа. 3,14 0,08 Первоначальный объем W жидкости равен: W = S 1 h + S 2 (H h) = h + (H h) = 0,093 м 3. Изменение объема равно: dw = S 2 h = h = 2,5 10 м 3. (1.7): Модуль объемной упругости определим по формулам (1.5) и Е о =W = 0,1 = 0, Па =1814 МПа., Контрольные вопросы. 1. В чем заключается гипотеза сплошности жидкости? 2. Что такое плотность жидкости, от чего она зависит? 3. Какие силы относятся к массовым и поверхностным? Какие виды напряжений действуют в жидкости? 4. В чем состоит физический смысл объемного модуля упругости? 5. Что такое вязкость жидкости? 6. Какова связь кинематической и динамической вязкости? 7. Поясните природу неньютоновских жидкостей. 8. Какие причины вызывают кавитацию? 9. Что такое «холодное» кипение? 10. Какова природа явления поверхностного натяжения? 22
21 Раздел 2 Гидростатика 2.1. Гидростатическое давление и его свойства. Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматриваются практические приложения этих законов. Рассмотрим некоторый объем жидкости массой М, находящийся в состоянии относительного покоя (рис. 2.1). Рассечем объем, занимаемый жидкостью, произвольной плоскостью АВ на две части, содержащие соответственно массы М 1 и М 2, и отбросим одну из них (например, правую). Чтобы сохранить равновесие оставшейся в левой части массы жидкости М 1, необходимо приложить силу, эквивалентную действию отброшенной массы М 2. Эта сила р будет равномерно распределена по площади сечения S. Тогда отношение р ср =, (2.1) представляющее собой среднюю силу, действующую на единицу площади S, будет называться средним гидростатическим давлением. Рис.2.1. Схема для определения гидростатического давления В общем случае величина среднего давления р ср будет тем меньше отличаться от истинного значения давления, например в точке а, чем меньше будет площадь сечения S, т.е. истинное гидростатическое давление равно: р а = lim S. (2.2) Сила, действующая на единицу площади S при стремлении (стягивании) этой площади к размерам точки А, называется силой гидростатического давления. Рассмотрим основные свойства гидростатического давления: 23
22 1.Сила гидростатического давления всегда направлена по нормали к площадке действия. Действительно, если бы сила р (рис.2.1) была направлена не по нормали к площадке S, то эту силу можно было бы разложить на составляющие: нормальную и касательную к площадке S. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, то есть в этом случае равновесие жидкости было бы невозможно. Поскольку жидкость не сопротивляется растягивающим усилиям (сопротивление растяжению может происходить только в дегазированных жидкостях), то сила р может быть только сжимающей. Таким образом, по любой поверхности, проведенной внутри покоящейся жидкости, всегда действует только распределенная сжимающая сила. 2.В покоящейся жидкости величина давления не зависит от ориентации в пространстве площадки, на которую она действует. Доказательство этого свойства сводится к определению равенства сил, действующих на боковые грани тетраэдра (рис.2.2), то есть: р х = р y = р z = р n. Доказательство этого равенства можно найти в любой учебной литературе по гидравлике. Рис.2.2 Схема для доказательства свойства гидростатического давления 3. Гидростатическое давление может быть неодинаковым в различных точках покоящейся жидкости, т.е. зависит от координаты точки в пространстве: р = f(x, y, z) Основное уравнение гидростатики. Рассмотрим случай равновесия жидкости, когда на нее действует лишь одна массовая сила сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Пусть на свободную поверхность жидкости, находящуюся в сосуде, действует давление р о (рис.2.3). 24
23 Рис 2.3 Схема для вывода основного уравнения гидростатики Определим давление р в произвольно выбранной точке М, которая находится на глубине h. Выделим около точки М элементарную (бесконечно малую) площадку ds, и построим на ней до свободной поверхности вертикальный цилиндрический объем высотой h. Вес жидкости в указанном объеме равен: G = Mg = ρ g h ds. (2.3) Давление жидкости р на нижнее основание цилиндра будет направлено по нормали вверх. Запишем сумму сил, действующих на выделенный объем в проекции на вертикальную ось: рds — р о ds ρghds = 0 После сокращения выражения на ds и перегруппировки членов получим: р = р о + ρgh = р о + γh. (2.4) Полученное уравнение называют основным уравнением гидростатики, оно позволяет подсчитать давление в любой точке внутри покоящейся жидкости. Из уравнения (2.4) видно, что давление р о, действующее на свободной поверхности жидкости, будет передаваться в любую точку внутри жидкости по всем направлениям одинаково (последнее утверждение вытекает из свойства гидростатического давления). Это позволяет сформулировать закон Паскаля: давление, приложенное к жидкости, передается по всем направлениям без изменения. Величину ρhg называют весовым давлением, т.к. она равна весу столба жидкости при единичной площади и высоте h. Основное уравнение гидростатики можно записать иначе. Пусть необходимо определить давление р в точке М на уровне z (рис. 2.3). Подставив в уравнение (2.4) значение высоты h = z о z, получим: р = р о + ρg (z о z). 25
24 После несложных преобразований получим основное уравнение гидростатики для двух точек одного и того же объема покоящейся жидкости: z 0 + = z +. (2.5) Поскольку точка М взята произвольно, то можно утверждать, что для всего рассматриваемого неподвижного объема жидкости: z + = const. (2.6) Таким образом, по формуле (2.4) в покоящейся жидкости в точке, находящейся на глубине h под свободной поверхностью, давление равно сумме внешнего давления р о и весового давления ρhg Геометрическая интерпретация основного уравнения гидростатики. Избыточное, вакуумметрическое и абсолютное давление. Измерение давления. Координата z рассматриваемой точки М жидкости (рис.2.3) отсчитывается от произвольной горизонтальной плоскости ОО, принятой в качестве координатной. В гидравлике эту плоскость называют плоскостью сравнения, а отсчитываемую от нее координату z точки геометрической высотой. Величина имеет линейную размерность и называется пьезометрической высотой. Сумма z + называется гидростатическим напором. Если давление на свободной поверхности жидкости равно атмосферному, то плоскость пьезометрического напора совпадает со свободной поверхностью жидкости. При р о р ат положения плоскости пьезометрического напора могут быть различными в зависимости от соотношения р о > р ат или р о р ат. Простейшим прибором жидкостного типа для измерения величины гидростатического давления является пьезометр, который представляет собой стеклянную трубку небольшого диаметра, открытую с одного конца и вторым концом присоединенную к сосуду, в котором необходимо измерить давление (рис.2.4). Согласно основному уравнению гидростатики (2.4), давление в точке М будет равно: р м = р о + ρgh = р ат + ρgh, откуда р о = р ат + ρg(h-h). (2.7) 26
25 Рис Схема измерения избыточного давления пьезометром Давление р о, определенное с учетом атмосферного давления, называется абсолютным давлением (2.7). Давление р о, действующее на свободной поверхности жидкости в сосуде, превышает атмосферное давление на величину ρg (H-h).Это давление называется избыточным давлением (2.8): р изб = р о — р ат = ρg (H-h). (2.8) Недостаток до атмосферного давления называется вакуумметрическим давлением (2.9). Взаимосвязь между абсолютным, избыточным и вакуумметрическим давлением изображена на рис.2.5 (а и б). Рис Взаимосвязь между давлением: а) абсолютным и избыточным; б) абсолютным и вакуумметрическим Рассмотрим случай, когда давление внутри сосуда меньше атмосферного (рис.2.6). Гидростатическое давление в точке М равно: р м = р о + ρgh = р ат + ρgh. Принимая во внимание, что h>h, получаем: р о = р ат — ρg (h-h). Обозначим h вак = h — H, тогда: 27
26 р о = р ат — ρgh вак = р ат — р вак. р вак = — ρg h вак 27 При нормальном атмосферном давлении (0,1053 МПа) высота h мах равна: для воды 10,33 м; для бензина (ρ = 750 кг/м 3 ) 13,8 м; для ртути 760 мм. Итак, атмосферное давление, равное 760 мм. рт. ст., соответствует высоте ртутного столба, равном 760 мм. Подставив это значение в уравнение (2.7) при ρ рт = кг/м 3, получим атмосферное давление, равное 1, Па. Эта величина называется физической атмосферой. Она отличается от технической атмосферы, которая составляет 736 мм. рт. ст. (техническая атмосфера равна давлению, возникающему при действии силы в 1кгс на площадь размером 1см 3 : 1 ат =1 кгс/см 2 ). Ртутные манометры. Пьезометр является очень чувствительным и точным прибором, однако он удобен для измерения небольших давлений; при больших давлениях трубка пьезометра получается чрезмерно длинной. В этих случаях применяют жидкостные манометры, в которых давление уравновешивается жидкостью большего удельного веса. Обычно такой жидкостью является ртуть (рис.2.8). Рис Схема ртутного манометра. По основному уравнению гидростатики (2.4): р а = р о + γ 1 h 1 = р ат + γ рт h рт, откуда р о = р ат — γ 1 h 1 + γ рт h рт. В тех случаях, когда необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или же в двух точках жидкости в одном и том же сосуде, применяют дифференциальные манометры (рис.2.9). 29
28 Рис Дифференциальный манометр По основному закону гидростатики для точки А: р а = р 1 + γh 1 = р 2 + γh 2 + γ рт h рт. Разность давлений р 1 — р 2 = γ (h 1 — h 2 ) + γ рт h рт. Для измерения давления вакуума ртутные манометры (вакуумметры) принципиально ничем не отличаются от обычных (рис.2.10). Рис Схема вакуумметра В этом случае р а = р вак + γ рт h рт = р ат, р вак = γ рт h рт р ат — γ рт h рт. Для измерения давлений более 0,2 0,3 МПа применяют механические манометры — пружинные или мембранные. Наряду с механическими применяют и электрические манометры. 30
29 2.4. Относительный покой (равновесие жидкости в движущемся сосуде). При равновесии в движущемся сосуде жидкость движется вместе с сосудом как единое целое, т.е. находится в состоянии относительного покоя. В этом случае на жидкость кроме массовой силы (силы тяжести) действует вторая массовая сила сила инерции переносного движения. Возможны два случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно; и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью. В обоих случаях поверхности уровня, т.е. поверхности равного давления (в том числе и свободная поверхность жидкости) принимают такой вид, при котором равнодействующая массовая сила нормальна к этим поверхностям во всех их точках. Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости с единичной массой. Таким образом, на каждую частицу жидкости с массой m =1 действуют сила тяжести G = g и сила инерции F ин = a. Прямолинейное движение. Рассмотрим сосуд, движущийся прямолинейно и горизонтально с постоянным ускорением (или замедлением) а (рис.2.11). Равнодействующая единичных силы тяжести g и силы инерции а нормальна по отношению к свободной поверхности и будет равна: = +. Рис Схема действия сил при прямолинейном движении сосуда Уравнение, позволяющее находить давление в лютой точке рассматриваемого объема жидкости (например, в точке М), можно получить аналогично тому, как это сделано в п.2.2. Давление в произвольной точке М на расстоянии l от свободной поверхности будет равно: р м = р o + l g j. 31
30 Это уравнение является частным случаем основного уравнения гидростатики. Действительно, при а = 0 следует, что j = g. Тогда с учетом l = h получаем формулу (2.4), то есть основной закон гидростатики. Цилиндрический сосуд, вращающийся относительно вертикальной оси. Рассмотрим цилиндрический сосуд радиусом R, вращающийся с постоянной угловой скоростью ω (рис.2.12). Рис Схема действия сил при вращении сосуда (общий случай) Уравнение поверхности уровня (в частности, свободной поверхности жидкости в сосуде) в цилиндрических координатах (r o,z 0 ) имеет вид: z = z o + ² ², (2.11) где z o вертикальная координата вершины параболы (высота жидкости на оси вращения), r, z координаты любой точки поверхности уровня. Формула для определения давления (например в точке М) в любой точке жидкости, находящейся в относительном покое, будет выглядеть так: р = р о + [(z o z) + ² ² ]ρg. (2.12) Если принять ω = 0 и обозначить h = z o z, то можно получить основной закон гидростатики (2.4). На практике часто встречается другой случай вращение сосуда с очень высокой скоростью (например, центрифуга). В этом случае центробежные силы гораздо больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда, а ее свободная поверхность располагается на радиусе r o (рис.2.13). 32
31 Рис Схема положения жидкости при вращении сосуда Тогда формула для определения давления примет вид: р = р о + ²( ₀²) ρ. (2.13) Повышение давления в жидкости, возникающее вследствие ее вращения, равно: р = р о + ² ρ. (2.14) 2.5. Примеры. При решении задач по гидростатике необходимо различать такие понятия, как давление р и сила F. Применяя основное уравнение гидростатики нужно помнить, что второй член в правой части уравнения может быть как положительным, так и отрицательным. Необходимо также твердо различать давления абсолютное, избыточное и вакуумметрическое, а также весовое давление жидкости. При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, то есть равенство нулю суммы всех сил, действующих на поршень или систему поршней. В задачах на относительный покой жидкости следует учитывать повышение давления за счет силы инерции переносного движения В цилиндрический бак диаметром 2 м до уровня Н = 1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить вес находящегося в баке бензина, если ρ б = 700 кг/м 3. 33
32 Весовое (избыточное) давление воды и бензина в баке будет равно весовому давлению воды в пьезометре: ρ в gh в + ρ б gh б = ρ в g(h h). Поскольку в этом уравнении есть два неизвестных, выразим h в = H h б, и подставим: ρ в g (H h б ) + ρ б gh б = ρ в g (H h). После сокращения получим: h б (ρ в ρ б ) = ρ в h. Высота бензина в баке: в, h б = = 1м. в б = Вес находящегося в баке бензина: G = Mg = ρ б g S h б = ρ б g π R 2 h б = 700 9,8 3, = 21,54 кн Определить давление р o воздуха в напорном баке по показанию ртутного манометра. Какой высоты Н должен быть пьезометр для измерения того же давления р o? Высоты h=2,6 м; h 1 =1,8 м; h 2 =0,6 м. Плотность ртути ρ= кг/м 3, воды ρ= 1000 кг/м 3. Абсолютное давление в баке на уровне высоты h 2 будет равно абсолютному давлению в ртутном манометре на том же уровне: р а = р о +ρ в g (h h 2 ) = р ат +ρ рт g(h 1 h 2 ). 34
33 р o = р ат +ρ рт g(h 1 h 2 ) — ρ в g (h — h 2 ) = ,8 1, ,8 2= = 240,3 кпа. Для нахождения высоты Н рассуждения аналогичны: р ат +ρ в g Н = р о +ρ в g h, в ат,, откуда Н = = = 16,92 м., в Определить силу F, действующую на шток гибкой диафрагмы, если ее диаметр D = 200 мм, показания вакуумметра р вак = 0,05 МПа, высота h = 1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если h a = 740 мм. рт. ст. Действующее на шток диафрагмы давление вакуума определяется по показанию вакуумметра с учетом высоты столба воды h: р вак.д. = ρgh р вак =1000 9, = Па. Знак » » указывает на то, что давление в левой полости гидроцилиндра по оси штока ниже атмосферного (давление вакуума). Атмосферное давление составляет: р ат = ,3 = Па. Абсолютное давление в левой полости (давление с учетом атмосферного давления): р аб = р ат р вак.д. = = Па. Сила, действующая на шток диафрагмы, равна: F = р вак ² = 40200,, ² = 1,26 H Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке масло с плотностью ρ = 870 кг/м 3. Диаметры D =80 мм; d = 30 мм; высота Н = 1000 мм; избыточное давление р 0 = 10 кпа. 35
34 Избыточное давление, действующее на кольцевую поверхность поршней, будет равно: р изб = р 0 + ρgн = ,8 1 = 18,5 кпа. Силы, действующие на кольцевые площади поршней с диаметрами D =80 мм и d = 30 мм, будут равны: F 1 = р изб (D d ш ). F 1 = р изб (d d ш ). Сила, сжимающая пружину, будет равна: F = F 1 F 2 = р изб (D d ) = , (0,08 2 0,03 2 ) = 79,87 Н Определить силу F, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой, а размеры трубы: D =100 мм; Н = 0,5 м; h = 4м. Длины рычага: а = 0,2 м и b =1 м. Собственным весом поршня пренебречь. Логично предположить, что сила F, необходимая для удержания поршня в равновесии, должна соответствовать давлению под ним, то есть весовому давлению столба жидкости: 36
35 р = ρg(н + h) = ,8 (0,5 + 4) = 44,1 кпа. Сила F в соответствии с длинами плеч рычага равна: F = р ² =, ,, ² = 69,2 Н Топливный бак автомобиля длиной L = 0,6 м, шириной b = 0,5 м и высотой Н = 0,2 м движется с ускорением а = 3,27 м/с 2. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака, высота h = 10 мм. Изобразим положение бензина в баке с минимальным объемом. Обозначим стороны прямоугольного треугольника как l и у. То-, tg α = =, = 0,33367., х = = = 0,03 м., гда: l = х + = 0,03 +, = 0,33 м у = l tg α = 0,33 0,33367 = 0,11 м. 37
36 Объем минимального количества бензина в баке, обеспечивающего его подачу без подсоса, будет равно: W =Sb = lу b =,, 0,5 = 9,1 л На рисунке показан элемент одной из возможных схем гидроусилителя сцепления автомобиля (трактора). Масло под давлением р 0 = 0,5 МПа подводится внутри вала и затем через отверстие в полость между двумя совместно вращающимися цилиндром А и поршнем Б, который может скользить вдоль вала. Давление масла, увеличенное благодаря действию центробежных сил, заставляет поршень перемещаться вправо и обеспечивает этим силу нажатия, необходимую для включения сцепления. Определить силу давления масла на поршень Б, если его диаметр D =120 мм; диаметр вала d = 20 мм; частота вращения n = об/мин; плотность жидкости ρ = 920 кг/м 3. Определим угловую частоту вращения:, ω = = = 628 рад/с. Увеличение давления за счет центробежной силы (уравнение 2.14) будет увеличиваться пропорционально увеличению расстояния от центральной оси элемента. В этом случае за увеличение давления примем его среднее значение: р = ω 2 ρ(r 2 +r 2 ) 2 2 = (,, ) =335,62 кпа. Давление в полости элемента с учетом увеличения давления за счет действия центробежной силы будет равно: р = р 0 + р = = 835, 62 кпа. Тогда сила, с которой действует давление р на поршень, будет равна: 38
37 F = р (D 2 + d 2 ) = , (0,12 2 0,02 2 ) = 9,2 кн В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2м. Определить, до какой угловой скорости можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если диаметр сосуда D = 100 мм. Уравнение свободной поверхности жидкости имеет вид (2.11): Н = z 0 +, где z 0 вертикальная координата вершины параболоида. Объем параболоида вращения W п равен: W п = πr 2 (Н z 0 ). Выразим объем жидкости W ж, находящейся в сосуде объемом W с, учитывая объем параболоида W п : W ж = W с W п = Н πr 2 (Н z 0 ) = (Н + z 0 ). Поскольку можно вычислить объем жидкости W ж в сосуде, находящегося в состоянии покоя, то можно записать: h = (Н + z 0 ). h = (Н + z 0 ). z 0 = 2h Н. Угловую скорость ω можно выразить из уравнения свободной поверхности жидкости в сосуде (2.11): ω = (Н ) = (,, ),, = 39,6 рад/с. 39
38 Контрольные вопросы. 1. Дайте определение гидростатического давления. 2. Почему гидростатическое давление является функцией координат р = f(x,y,z)? 3. Что такое весовое давление жидкости? 4. Может ли давление в жидкости быть меньше нуля, равно нулю? 5. В каких случаях плоскость пъезометрического напора располагается выше или ниже свободной поверхности покоящейся жидкости? 6. Что такое абсолютное, избыточное и вакуумметрическое давление? 7. Как можно измерить атмосферное давление? В чем разница между физической и технической атмосферой? 8. Может ли движущаяся жидкость находиться в состоянии покоя? Если может, то при каких условиях? 40
📸 Видео
Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

Закон БернуллиСкачать

10. Уравнения БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Формула БернуллиСкачать

Уравнение Бернулли Метод БернуллиСкачать

ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Урок 15. Схема Бернулли. Решение задачСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Уравнение Бернулли для потока жидкостиСкачать

Формула БернуллиСкачать

Закон Бернулли. Примеры задачСкачать

Гидродинамика. Уравнение Бернулли. Физика 10 классСкачать

Урок гидравлики - 01 - Основные положенияСкачать






















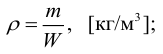
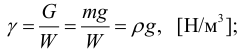
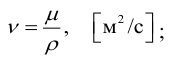
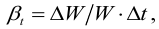
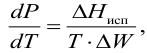
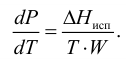
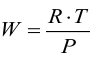
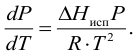
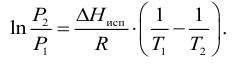
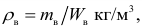
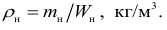
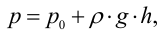
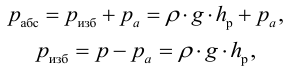
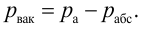
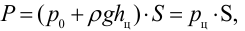
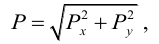
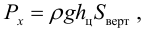
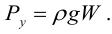
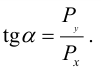
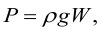
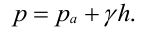
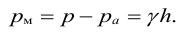
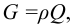
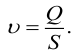
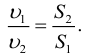
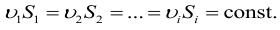
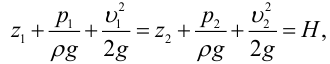
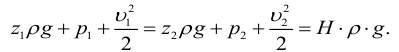
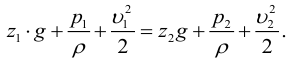
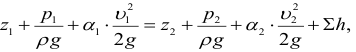
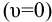 );
);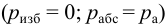 ;
;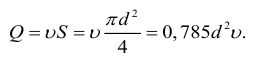
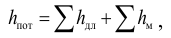
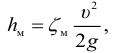
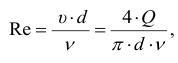
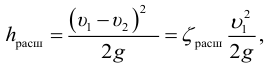
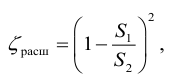
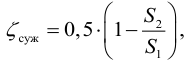
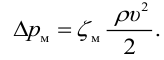
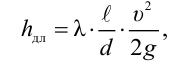
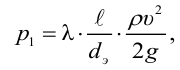
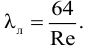
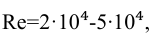
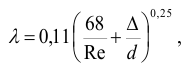
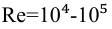
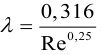
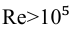
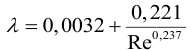
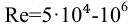
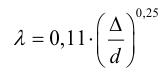
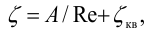
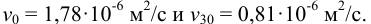
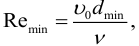
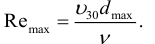
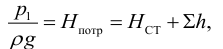
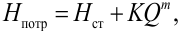
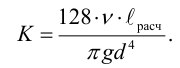
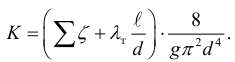
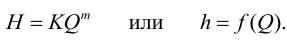
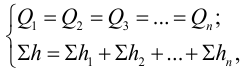
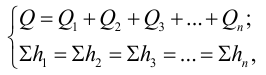
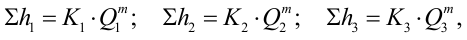
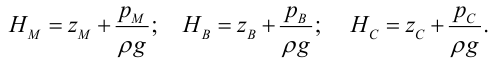
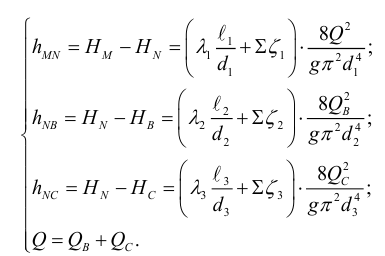
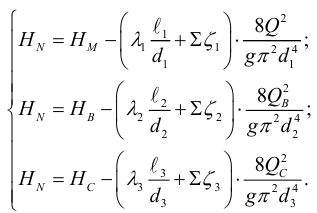
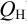 ) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса, 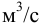 ;
;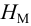 называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;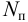 — это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом 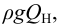 полезную мощность можно выразить:
полезную мощность можно выразить: