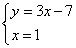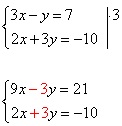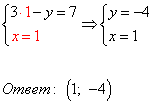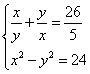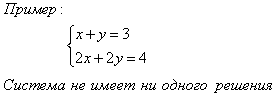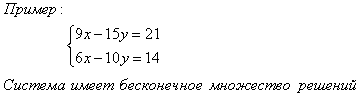Примеры решения системы уравнений методом введения новой переменной

Видео:Решение уравнения методом замены переменнойСкачать

Тестирование онлайн

Видео:Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Видео:Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Видео:Решение системы нелинейных уравнений методом введения новой переменной. 9 класс алгебра.Скачать

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Видео:§101 Метод введения новой переменнойСкачать

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену 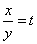, тогда

Переходим к первоначальным переменным

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если 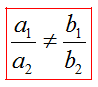, то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Видео:Решение рациональных уравнений методом введения новой переменной | Алгебра 8 класс #37 | ИнфоурокСкачать

Метод Гаусса*

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Метод введения новых переменных

Метод введения новых переменных

учитель школы «Логос ЛВ», ст. преп. фак-та довузовской подготовки МИТХТ, г. Москва

Тема: Системы уравнений

Урок: Метод введения новых переменных

1. Тема урока, введение

На предыдущих уроках для решения систем уравнений применялись графический метод, метод подстановки и метод алгебраического сложения. Сейчас будет рассмотрен метод введения новых переменных.

2. Пример на введение новых переменных

Введение новых переменных позволяет упростить исходную систему. Рассмотрим в качестве примера систему, которая предлагалась на вступительном экзамене в 1979 г. в МГУ на механико-математический факультет.

Пример 1. Решить систему

Полезно ввести новые переменные

Довольно сложная исходная система свелась к более простой. Это система двух линейных уравнений относительно a и b. Решим ее методом алгебраического сложения, вычтем из первого уравнения второе.

Мы ввели новые переменные и решили систему относительно этих переменных. Возвращаемся к старым переменным.

Мы получили вторую систему двух линейных уравнений относительно x и y.

Решим систему методом подстановки.

Ответ:

3. Основные сведения о квадратных уравнениях

Часто при замене переменных мы получаем квадратное уравнение. Напомним основные сведения о них:

Квадратное уравнение в общем виде:

Формула корней квадратного уравнения через дискриминант:

Если b – четное число, имеем формулу:

Напомним теорему Виета: Если корни квадратного уравнения , то

Верно и обратное: Если числа удовлетворяют системе , то они являются корнями квадратного уравнения .

Напомним прием, который позволяет упростить нахождение корней квадратного уравнения. Умножим квадратное уравнение на Получим

Получили новое уравнение относительно новой переменной

Мы получили приведенное квадратное уравнение с целыми коэффициентами (если они были целыми в исходном уравнении).

4. Примеры приведенных квадратных уравнений с заменой переменных

Пример 2. Решить уравнение

;

Это приведенное уравнение, коэффициенты – целые числа.

По теореме Виета

Ответ:

Пример 3. Решить уравнение

Получили приведенное квадратное уравнение относительно z.

По теореме Виета

Ответ:

Мы рассмотрели еще один прием, который позволяет упростить нахождение корней квадратного уравнения.

5. Решение систем уравнений

После сделанных напоминаний для квадратных уравнений решим систему:

Пример 4. Решить систему

Решение: Произведем замену:

Вернемся к исходной системе:

Ответ:

Пример 5. Решить систему:

Введем новую переменную: Получаем квадратное уравнение относительно новой переменной.

Исходная система свелась к совокупности двух систем:

Каждую систему решаем методом подстановки.

1.

2.

Находим y при известных x.

Ответ:

6. Пример симметрической системы

Следующая система – симметрическая. Симметрической называется такая система, которая не изменится, если переменные поменять местами.

Решение: Произведем замену

Мы ввели новые переменные, и нашли их.

Вернемся к старым переменным. Получаем две системы:

1.

2.

нет решений.

Ответ:

Заметим, что решением симметрической системы являются симметричные пары чисел.

Мы рассмотрели метод введения новых переменных. На следующем уроке рассмотрим системы повышенной сложности.

Список рекомендованной литературы

1. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / , и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев . 9 класс : учеб. для учащихся общеобразоват. учреждений / , , . — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. , , Сидоров . 9 класс. 16-е изд. — М., 20с.

5. Мордкович . 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / , . — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / , , и др.; Под ред. . — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы

1. Раздел ***** по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

Рекомендованное домашнее задание

1. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / , и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 000, 129.

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Методы решения систем уравнений с двумя переменными

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) ( left< begin mathrm & \ mathrm & endright. )
Решаем методом подстановки: ( left< begin mathrm & \ mathrm & endright. )
Для нижнего уравнения: ( mathrm )
Подставляем в верхнее уравнение: ( mathrm )

б) ( left< begin mathrm & \ mathrm & endright. )
Замена переменных: ( left< begin mathrm & \ mathrm & endright. )
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: ( left< begin mathrm & \ mathrm & endright.Rightarrow left< begin mathrm & \ mathrm & endright. )
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ mathrm< D=9^2-4cdot 2cdot 10=1, b=frac> = left[begin mathrm & \ mathrm & endright. $$ Возвращаемся к исходным переменным: ( left[begin left<begin mathrm & \ mathrm & endright.& \ left<begin mathrm & \ mathrm & endright. endright. )

🔥 Видео

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем уравнений методом подстановкиСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Решение уравнений методом введения новой переменнойСкачать

Пример 47. Решить систему методом замены переменнойСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение систем уравнений методом сложенияСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать