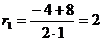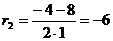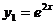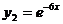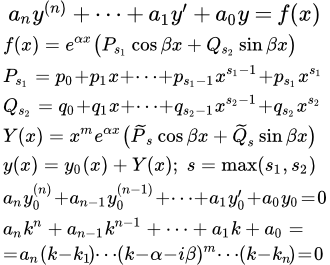Примеры решения дифференциальных уравнений с косинусом

y» +4y’ — 12y = 8sin(2x)

Решение уравнения будем искать в виде y = e rx находим с помощью калькулятора. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +4 r — 12 = 0
D = 4 2 — 4 • 1 • (-12) = 64


Корни характеристического уравнения:
r₁ = 2
r₂ = -6
Следовательно, фундаментальную систему решений составляют функции:


Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = 8•sin(2•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 8, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2•B•cos(2x)-2•A•sin(2x)
y» = -4(A•cos(2x)+B•sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y» + 4y’ -12y = (-4(A•cos(2x)+B•sin(2x))) + 4(2•B•cos(2x)-2•A•sin(2x)) -12(Acos(2x) + Bsin(2x)) = 8•sin(2•x)
или
-8•A•sin(2x)-16•A•cos(2x)-16•B•sin(2x)+8•B•cos(2x) = 8•sin(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-8A -16B = 8
-16A + 8B = 0
Решая ее, методом Гаусса находим:
A = -1 /₅;B = -2 /₅;
Частное решение имеет вид:
y * = — 1 /₅cos(2x) — 2 /₅sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 2.
4y’’ -8y’ + 5y = 5cos(x)
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
4 r 2 -8 r + 5 = 0
D = (-8) 2 — 4 • 4 • 5 = -16


Корни характеристического уравнения:
(комплексные корни):
r₁ = 1 + 1 /₂i
r₁ = 1 — 1 /₂i
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x cos( 1 /₂x)
y₂ = e x sin( 1 /₂x)
Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = 5cos(x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 5, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Acos(x) + Bsin(x)
Вычисляем производные:
y’ = Bcos(x)-Asin(x)
y» = -Acos(x)-Bsin(x)
которые подставляем в исходное дифференциальное уравнение:
4y» -8y’ + 5y = 4(-Acos(x)-Bsin(x)) -8(Bcos(x)-Asin(x)) + 5(Acos(x) + Bsin(x)) = 5cos(x)
или
8Asin(x)+Acos(x)+Bsin(x)-8Bcos(x) = 5cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A + B = 0
A -8B = 5
Решая ее методом Гаусса, находим:
A = 1 /₁₃;B = -8 /₁₃;
Частное решение имеет вид:
y * = 1 /₁₃cos(x) + -8 /₁₃sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 3.
y»+3y’+2y=-24e -4x -20sin(2x)
Решаем в два этапа:
а) y»+3y’+2y=-24e -4x
б) y»+3y’+2y=-20sin(2x)
Затем объединяем полученные решения.

Видео:Дифференциальные уравнения: пример 1Скачать

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Определение общего решения по известному частному решению

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Вначале ищем общее решение однородного уравнения:
(3) .

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Установление вида частного решения

Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .

Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .

Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .

Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).

Если среди корней характеристического уравнения (4) есть корень кратности p со значением

то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.

Видео:Пример 65. Решить задачу Коши (диффуры)Скачать

Частные случаи

Неоднородность в виде многочлена

Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.

Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020

Видео:Дифференциальные уравнения. 11 класс.Скачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

🔥 Видео

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

6. Особые решения ДУ первого порядкаСкачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Задача Коши, примеры, решение дифференциального уравненияСкачать