Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
Что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
Xi=φ(xi-1) , i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула — формулой итерационного процесса метода.
Если 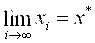
Условие сходимости 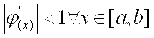
Точное решение x* получить невозможно, так как требуется Бесконечный Итерационный процесс.
Можно получить Приближенное Решение, прервав итерационный (3.8) при достижении условия
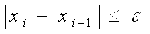
Где ε — заданная точность; i — номер последней итерации.
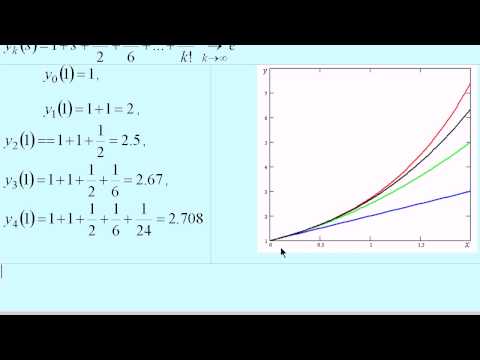
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Рис. 3.7 Итерационный процесс для случая 0 1 
 |
Рис. 3.10 Итерационный процесс для случая 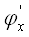
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
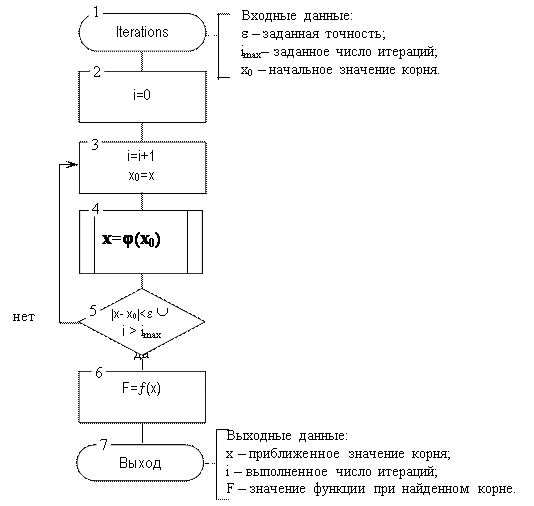 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .
Простейшие эквивалентные преобразования, например:
F(x) = 0 => x+f(x) = x, т. е. φ(x) = x + f(x)
Или выразить явно x из (3.1)
F(x) = 0 => x — φ(x) = 0 => x = φ(x)
Не гарантируют сходимость.
Рекомендуется следующий способ получения формулы Сходящегося итерационного процесса.
Пусть 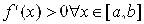
Если это не так, переписать уравнение (3.1) в виде
Умножить обе части уравнения на 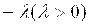
Константу l вычислить по формуле:
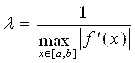
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
Xi = xi+1− λ f(x) (3.12)
Где i=1,2,… — номер итерации, x0Î[a, b] – начальное приближение.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
Проверим условия сходимости для полученной формулы:
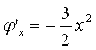
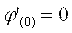
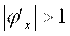
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
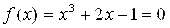
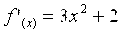
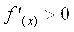
Наибольшее значение 
Следовательно 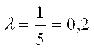
Формула Сходящегося итерационного процесса
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение
Проверим условие завершения итерационного процесса
Расчет следует продолжить.
X6 = 0,453917 − ответ, т. к.
Проверим полученное значение, подставив в исходное уравнение:
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
Видео:Метод итераций (последовательных приближений)Скачать

Метод итераций
Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Видео:5. Метод последовательных приближенийСкачать
Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Видео:Решаем диффуры методом последовательных приближенийСкачать

Метод последовательных приближений решения дифференциального уравнения
Пусть требуется найти решение дифференциального уравнения
Будем предполагать, что в некотором прямоугольнике для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).
Решение задачи (1)-(2) может быть найдено методом последовательных приближений , который состоит в следующем.
Строим последовательность функций, определяемых рекуррентными соотношениями
В качестве нулевого приближения можно взять любую функцию, непрерывную в окрестности точки , в частности — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале , где
Оценка погрешности, получаемой при замене точного решения n-м приближением , даётся неравенством
где . Применяя метод последовательных приближений, следует остановиться на таком , для которого не превосходит допустимой погрешности.
Пример 1. Методом последовательных приближений найти решение уравнения , удовлетворяющее начальному условию .
Решение. Очевидно, что для данного уравнения на всей плоскости выполнены условия теоремы существования и единственности решения задачи Коши. Строим последовательность функций, определяемых соотношениями (3), приняв за нулевое приближение :
Ясно, что при . Непосредственной проверкой убеждаемся, что функция решает поставленную задачу Коши.
Пример 2. Методом последовательных приближений найти приближенное решение уравнения , удовлетворяющее начальному условию в прямоугольнике
Решение. Имеем , т. е. . За берем меньшее из чисел , т. е. . Последовательные приближения согласно (4) будут сходится в интервале . Составляем их
Абсолютная погрешность третьего приближения не превосходит величины
Замечание. Функция должна удовлетворять всем условиям теоремы существования и единственности решения задачи Коши.
Следующий пример показывает, что одной непрерывности функции недостаточно для сходимости последовательных приближений.
Пусть функция определена следующим образом:
На множестве , функция непрерывна и ограничена постоянной . Для начальной точки последовательные приближения при имеют вид:
Поэтому последовательность для каждого не имеет, предела, т. е. последовательные приближения не сходятся. Заметим также, что ни одна из сходящихся подпоследовательностей и не сходится к решению, поскольку
Если же последовательные приближения сходятся, то полученное решение может оказаться неединственным , как показывает следующий пример: .
Возьмем начальное условие ; тогда
Беря в качестве нулевого приближения функцию , будем иметь
так что все последовательные приближения равны нулю и поэтому они сходятся к функции, тождественно равной нулю. С другой стороны, функция представляет собой также решение этой задачи, существующее на полупрямой .
🌟 Видео
Метод Пикара последовательных приближений для решения дифференциальных уравненийСкачать

Интегральные уравнения Вольтерра второго рода Метод последовательных приближенийСкачать

Метод простой итерации Пример РешенияСкачать

Острые диффуры, или как научиться решать методом последовательных приближенийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Метод последовательного приближения или от простого к сложномуСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Решение биквадратных уравнений. 8 класс.Скачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Решение уравнения методом замены переменнойСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

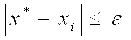
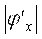
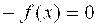
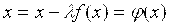
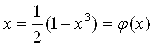
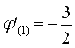

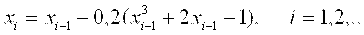
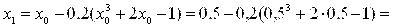
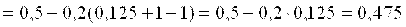
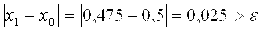
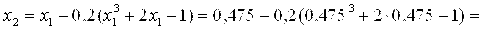
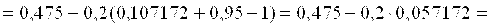
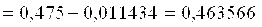
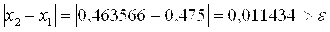
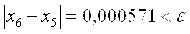
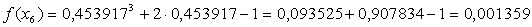
 ≡ x^2/(1+x)
≡ x^2/(1+x)