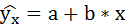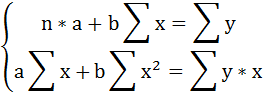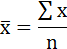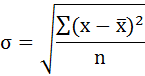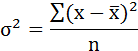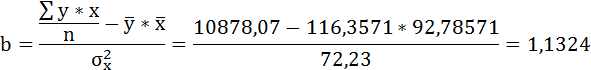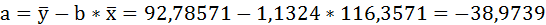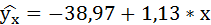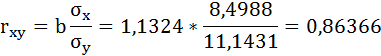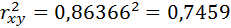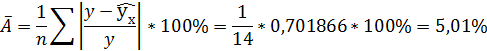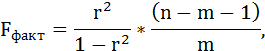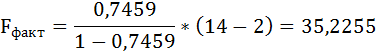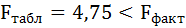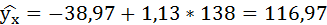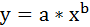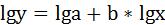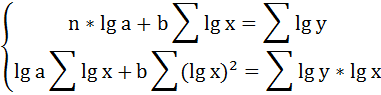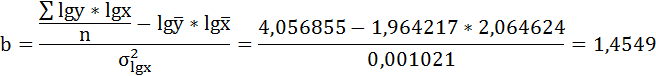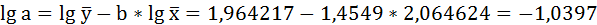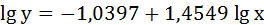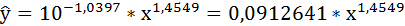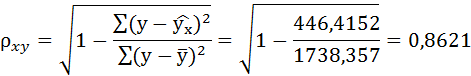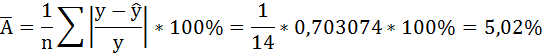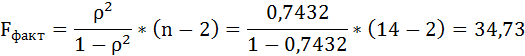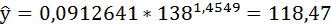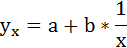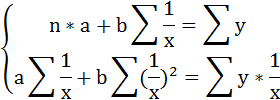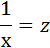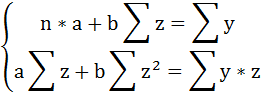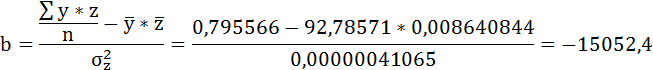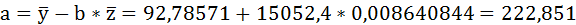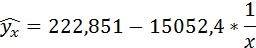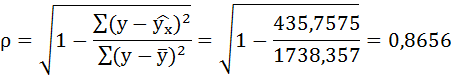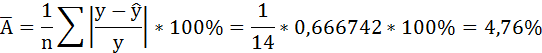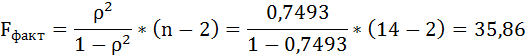- Что такое регрессия?
- Линия регрессии
- Метод наименьших квадратов
- Предположения линейной регрессии
- Аномальные значения (выбросы) и точки влияния
- Гипотеза линейной регрессии
- Оценка качества линейной регрессии: коэффициент детерминации R 2
- Применение линии регрессии для прогноза
- Простые регрессионные планы
- Пример: простой регрессионный анализ
- Задача исследования
- Просмотр результатов
- Коэффициенты регрессии
- Распределение переменных
- Диаграмма рассеяния
- Критерии значимости
- Уравнение регрессии
- Задача №1 Построение уравнения регрессии
- Требуется:
- Решение:
- 🔍 Видео
Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Видео:Парная регрессия: линейная зависимостьСкачать

Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Между
и
существует линейное соотношение: для любых пар
данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.
- Остатки нормально распределены с нулевым средним значением;
- Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин
Если нанести остатки против предсказанных величин
от
мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением
то это допущение не выполняется;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Видео:РегрессияСкачать

Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Видео:Регрессия. ПримерСкачать

Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Видео:Множественная регрессия в ExcelСкачать

Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Видео:Линейная регрессияСкачать

Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
Видео:Математика #1 | Корреляция и регрессияСкачать

Уравнение регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 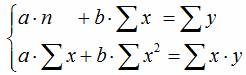
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:
Видео:Практика Многофакторная регрессияСкачать

Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 |  |  |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 | 8,4988 | 11,1431 | х | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 
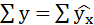
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 | 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 | 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 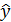
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 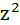 | 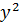 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 | 8,4988 | 11,1431 | 0,000640820 | х | х | х |
 | 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
🔍 Видео
Пример проверки гипотезы о незначимости регрессииСкачать

Множественная регрессияСкачать

Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Лекция 8. Линейная регрессияСкачать

Эконометрика. Линейная парная регрессияСкачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать