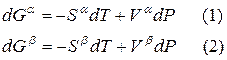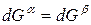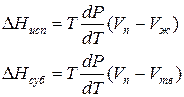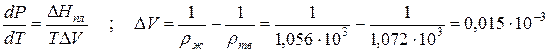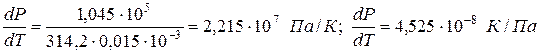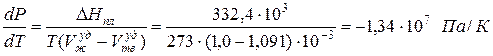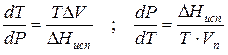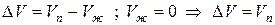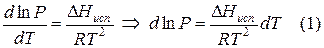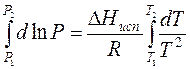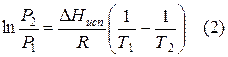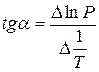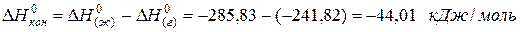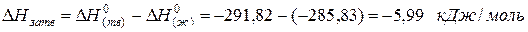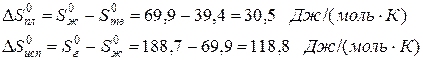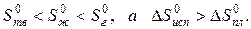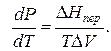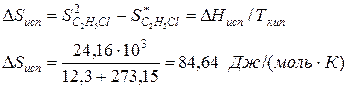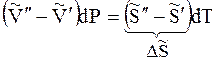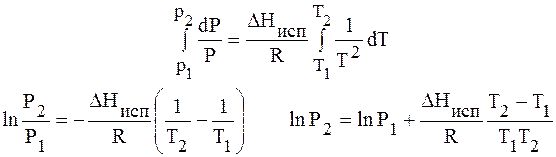ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.
УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.
Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:
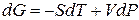
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать
Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.
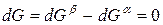
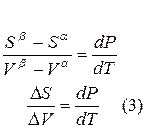
Для равновесного обратимого процесса согласно уравнениям 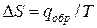
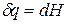
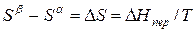
а уравнение (3) примет вид
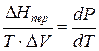
где ∆Hпер – теплота фазового перехода.
Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:
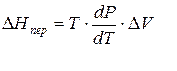
Клапейрона–Клаузиуса
где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.
Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.
Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:
где ∆Hисп , ∆Hсуб – теплоты испарения и сублимации; Vп, Vж, Vтв – мольные объемы пара, жидкости и твердого тела соответственно.
В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.
Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Тпл. Плотность твердого фенола ρтв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆Hпл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:
Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Тпл = 314,2+2,29 = 316,49 К.
Следует иметь в виду, что в процессе плавления у большинства веществ Vж > Vтв , тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.
Однако, такие вещества как вода (Н2О), висмут (Bi), имеют объем твердой фазы Vтв больше, чем объем жидкой фазы Vж уд = 10 -3 м 3 /кг и Vтв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆Hпл = 332,4 кДж/кг:
Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.
Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.
Уравнение для процесса испарения 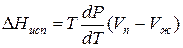
Пар подчиняется законам идеального газа: PV=RT 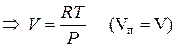
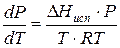
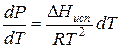
Проведем интегрирование уравнения (1) в пределах от Т1 до Т2 и соответственно от Р1 до Р2 при условии, что в области невысоких давлений пара ∆Нисп ≈ const; в результате интегрирования получим:
∆Нисп / R = const, выносим за знак интеграла
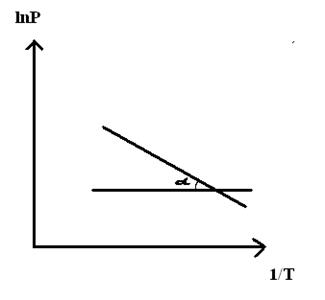
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р1 и Р2 и соответствующие им температуры испарения Т1 и Т2 . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен 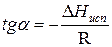
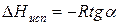
Расчетные значения ∆Нисп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Нисп определяют изменение давления при изменении температуры в процессе испарения.
Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.
Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет
для водяного пара ∆Н(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н(ж) 0 = -285,83 кДж/моль; для льда ∆Н(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:
а теплота превращения воды в лед:
Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.
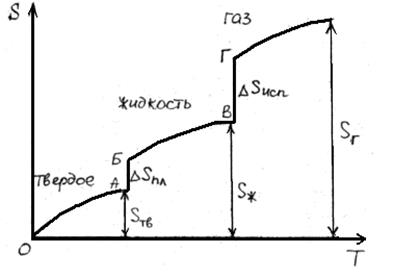
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.
Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.
Пример. Оценим скачок энтропии на примере фазовых переходов воды:
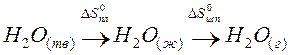
когда известны стандартные абсолютные значения энтропии Sтв 0 =39,4; Sж 0 =69,9; Sг 0 =188,7 Дж/(моль·К).
В соответствии с рисунком для воды
По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой
Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Нисп =24,16 кДж/моль.
Молекулярная масса 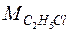
В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Нпер в соответствии с уравнением Клапейрона–Клаузиуса.
Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.
В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β 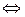
| | | следующая лекция ==> | |
| ДИАГРАММА СОСТОЯНИЯ СЕРЫ. | | | ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ. |
Дата добавления: 2016-02-02 ; просмотров: 3219 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Уравнение Клапейрона – Клаузиуса, применение его к однокомпонентным системам
Простейшим типом гетерогенного равновесия является равновесие чистого вещества со своим насыщенным паром, т.е. равновесие
Такое равновесие можно изобразить графически:
давление насыщенного пара — температура
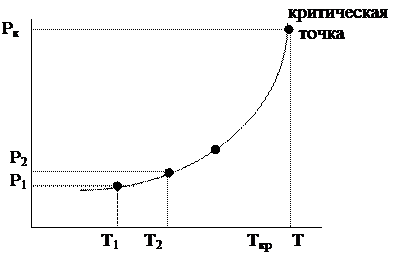 |
Рис. 6.20. Зависимость давления от температуры
Давление насыщенного пара – это равновесное давление, которое создается при Т = const некоторым количеством вещества в закрытом сосуде, не содержащем посторонних газов.
Давления насыщенного пара при разных температурах дают кривую испарения.
Давления насыщенного пара над твердым веществом при разных температурах дают кривую возгонки (сублимации).
Верхняя точка кривой испарения – критическая точка.
Верхняя граница кривой возгонки – точка плавления.
Направление кривых испарения и возгонки определяется уравнением Клаузиуса – Клапейрона. Получим его.
Когда две фазы чистого вещества находятся в равновесии, их изобарные потенциалы
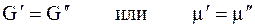
т.к. химический потенциал — это изобарный потенциал 1 моль вещества
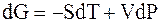
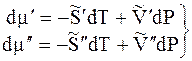
величины 
При равновесии 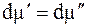
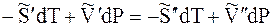
Отсюда 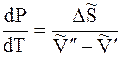
где DS – изменение энтропии при переходе 1 моль вещества из фазы 1 в фазу 2.
Из второго закона термодинамики известно, что для обратимых изотермических процессов
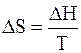
Подставим 6.244 в 6.243, получим уравнение Клапейрона –Клаузиуса (1850 г.)
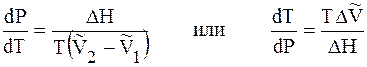
которое характеризует зависимость температуры фазового перехода от внешнего давления.
Уравнение Клапейрона – Клаузиуса описывает фазовые переходы I рода, к которым относятся переходы вещества из одного агрегатного состояния в другое, переходы из одной кристаллической модификации в другую. Среди них плавление, испарение, конденсация, возгонка,
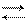
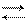
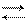
DH – теплота фазового перехода 1 моль вещества.
При фазовых переходах скачком изменяются молярная энтропия 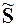
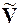
Рассмотрим некоторые конкретные случаи применения уравнения Клапейрона – Клаузиуса:
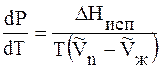
DH > 0, т.к. рассматривается переход жидкости в пар, энергия
T > 0 и 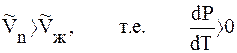
Это значит, что давление насыщенного пара растет с увеличением температуры.
Предположим, что пар подчиняется уравнению состояния идеального газа, т.е. 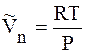
И если система далека от критической температуры, то 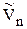
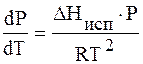
Разделим переменные и интегрируем, предполагая, что DHисп не зависит от Т.
или 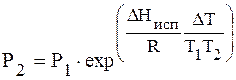
По этому уравнению можно рассчитать давление насыщенного пара Р2, зная Р1 и DHисп. Можно также рассчитать DHисп.
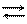
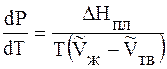
Разность DV мала, поэтому кривая плавления идет круто вверх.
Когда плотность твердого вещества больше плотности жидкого
DV > 0 и 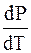
Когда плотность твердого вещества меньше плотности жидко-
У льда с повышением давления Тплав понижается, что объясняет скользкость льда (под давлением конька образуется вода, играющая роль смазки).
К = 1 S = 1 – ф + 2 ® S = 3 – ф
При равновесии в системе не может быть больше трех фаз, иначе число степеней свободы будет отрицательным числом, что не имеет физического смысла.
Т.е. в однокомпонентной системе одновременно могут существовать максимально три фазы: например, паровая, жидкая, твердая.
Диаграмму однокомпонентной системы (H2O) можно изобразить следующим образом.
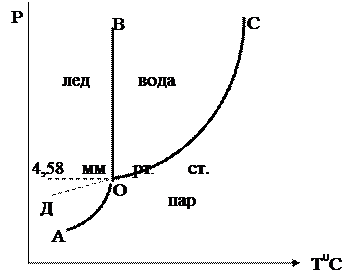 |
Рис. 6.21. Диаграмма состояния воды
В большинстве случаев за независимые переменные выбирают Р и Т.
Фазовой точкой называется точка на диаграмме, изображающая состояние одной фазы.
Совокупность фазовых точек, изображающих состояние одной фазы, называется фазовым полем
I – фазовое поле пара,
II – фазовое поле жидкости, III – твердая фаза.
Фазовые поля разделены фазовыми линиями:
ОС – соответствует равновесию двух фаз пар – жидкость,
ОА – пар – твердая фаза, ОВ – жидкость – твердая фаза.
В точке О в равновесии находятся все три фазы.
Число степеней свободы:
на фаз. поле S = 3 – 1 = 2 (два параметра можем менять),
на фаз. линии S = 3 – 2 = 1 ( один параметр можем менять),
в точке О S = 3 – 3 = 0 (параметры менять нельзя).
Если продлить ОС до Д, то ОД соответствует равновесию пар – переохлажденная жидкость.
Давление насыщенного пара над переохлажденной жидкостью больше, чем надо льдом, т.е. переохлажденная жидкость является неустойчивой (метастабильной) фазой относительно льда.
Диаграмма состояния с несколькими твердыми фазами. В однокомпонентной системе может быть только 1 паровая и 1 жидкая фаза, а твердых фаз может быть несколько. Например, сера в твердом состоянии существует в двух модификациях S(ромб) и S(монокл) с различной кристаллической решеткой, для Fe известны 4 модификации a-, b-, g- и d-, для воды известны более 5 твердых форм и т.д.
Каждая из этих модификаций выступает как отдельная самостоятельная фаза и на диаграмме ей соответствует отдельное фазовое поле.
Рассмотрим диаграмму состояния серы.
Рис. 6.22. Диаграмма состояния серы
В данном случае 4 фазовых поля, 6 фазовых линий и три тройных точки А, В и С.


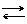
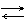
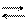
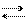
Равновесие всех четырех фаз не может быть осуществлено, т.к. число степеней свободы в этом случае S = 1 – 4 + 2 = –1, что противоречит действительности.
Энантиотропные и монотропные превращения.Многие вещества способны существовать в различных кристаллических модификациях, каждая из которых обладает определенными границами устойчивости. При этом существует некоторая температура перехода, выше которой устойчивой является одна из модификаций, а ниже – вторая.
Если превращение в точке перехода может самопроизвольно протекать как в прямом, так и в обратном направлениях, то такой переход называется энантиотропным (рис. 6.23). В этом случае между модификациями существует равновесие
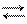
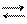
Примером энантиотропного фазового перехода может служить процесс взаимного перехода серы ромбической и серы моноклинической. Энантиотропные превращения наблюдаются только в таких системах, в которых температура взаимного перехода (точка О) обеих полиморфных модификаций ниже температуры плавления этих модификаций (точки О3, О4 на рис. 6.23).
 |
Рис. 6.23. Диаграмма состояния однокомпонентной системы
с энантиотропными фазовыми превращениями
Кривая равновесия жидкость – пар СС / расположена выше точки О пересечения кривых АА / и ВВ / равновесия соответственно a- и b-полиморфных модификаций с паром. В интервале температур, соответствующих точкам А и О, более устойчива a-модификация, т.к. давление пара на участке АО ниже, чем на участке ВО. В интервале температур между точками О и О4 более устойчивой является b-модификация, которой соответствует кривая ВВ / . Между точками О4 и С / устойчивой является жидкая фаза (кривая СС / ). Участки кривых, расположенные выше кривой АОО4С / , соответствуют неустойчивым метастабильным равновесным состоянием (отрезки ВО, ОА / , СО4, О4В / ). При повышении температуры выше Т0 более устойчивой будет b-модификация и a-модификация переходит в b-модификацию. При понижении температуры ниже Т0 происходит обратный переход.
Если при любых условиях одна из модификаций более устойчива, чем вторая, то возможен переход только второй модификации в первую, но не обратно.

т.е. вторая модификация образуется из жидкости, но не из первой модификации.
Превращение модификаций, которые могут протекать только в одном направлении, называются монотропными.
В таких системах переход от модификации, устойчивой при более высоких температурах, к модификации, устойчивой при более низких температурах, невозможен. Обратный переход осуществляется и протекает тем быстрее, чем выше температура. Примерами монотропных фазовых переходов являются: превращения a-бензофенона в b-бензофенон, белого фосфора в красный, неустойчивых модификаций мышьяка и сурьмы в устойчивые модификации и др.
 |
Рис. 6.24. Диаграмма состояния бензофенона
Рассмотрим диаграмму состояния бензофенона (С6Н5)2СО с монотропными превращения твердых фаз (рис. 6.24).
На этой диаграмме кривые аО, вО и КО изображают устойчивые двухфазные равновесия b — бензофенона. a — бензофенон является неустойчивой модификацией и может самопроизвольно превращаться в b-(C6Н5)2CО, тогда как обратный переход невозможен.
Линии аО и а¢О¢ отображают равновесия кристаллических b- и a-(C6Н5)2CО с паром, они должны пересечься в точке с, т.е. при температуре более высокой, чем температуры плавления этих модификаций (точки О и О¢). Так как перегреть кристаллическое вещество выше его температуры плавления невозможно, то линии сО и сО¢ продолжающие линии аО и аО¢, отражают физически нереальные состояния.
Рассмотренные закономерности фазовых равновесий и фазовых переходов имеют большое значение для химиков-технологов, т.к. позволяют установить оптимальный режим протекания химических и физико-химических процессов.
Видео:Коробов М. В. - Физическая химия. Часть 1 - Фазовые диаграммы. Фазовые переходыСкачать

Фазовые равновесия и фазовые переходы. Уравнение Клапейрона-Клаузиуса
Сначала рассмотрим условия равновесия изолированной двухфазной однокомпонентной системы вода-пар, на которую действует только всестороннее давление. Общее условие равновесия этой системы есть:
где г|’ и Г|» — энтропии соответственно воды и пара. С помощью уравнения (2.38) перепишем соотношение (6.9) в виде:
Учитывая, что экстенсивные параметры системы подчинены следующим уравнениям связей:
предыдущее выражение можно записать в виде:
Из этого уравнения находятся следующие частные условия фазового равновесия однокомпонентной системы:

Если T=const и p=const, то эти три условия можно записать в виде одного равенства химических потенциалов вещества в фазах:
При равенстве же двух фаз разных веществ должны выполняться условия
где верхний индекс означает фазу, а нижний — компонент, т. е. равенство температур и давлений в фазах. На химические потенциалы никаких условий в этом случае не накладывается, так как обмена частицами между такими фазами быть не может.
Из формул (6.10) и (6.12) можно сделать общий вывод, что при равновесии гетерогенной системы из п фаз с к компонентами температура, давление и химические потенциалы каждого компонента во всех фазах одинаковы.
Это позволяет определить количество фаз (состоящих из нескольких компонентов), способных одновременно находится в равновесии (число независимых переменных гетерогенной системы), которые можно изменять, не нарушая ее равновесия. Эта задача была решена Дж. Гиббсом, который установил, что в системе из к компонент одновременно в равновесии может находиться не больше, чем к+2 Лазы:
Выражение (6.13) называется правилом фаз Гиббса. Это правило получено для гетерогенной системы, на которую действует только одна сила давления. Соотношение (6.13) можно записать в виде:
где / — число термодинамических степеней свободы системы (число независимых переменных, которые могут быть произвольно изменены без нарушения равновесия гетерогенной системы).
При равновесии двух фаз (я=2) системы с одним компонентом (Л=1) число степеней свободы f=. Этот вывод можно получить и из равенства (6.11), которое связывает температуру и давление в фазах. Одну из них можно взять за независимую переменную, тогда получим зависимость давления от температуры при равновесии:
На Тр-плоскости это будет соответствовать кривой равновесия фаз. При этом точки, лежащие по обеим сторонам этой кривой, представляют собой различные однородные состояния тела.
При равновесии трех фаз одного и того же вещества, например лед-вода-пар, число степеней свободы j= 0, т. е. равновесие в этом случае достигается только в одной точке на 7р-плоскости (рис. 6.1). Температуру и давление в этой точке можно получить из следующих уравнений:
Состояние, определяемое этими значениями переменных Т и р, называется тройной точкой. Тройная точка для пресной воды имеет следующие значения: 7H),0100 o С при р=509 Па. Для морской воды температура тройной точки выше температуры замерзания примерно на такую же величину.
При равновесном переходе вещества из одной фазы в другую, как и при фазовом равновесии, температура, давление и химический потенциал вещества в фазах одинаковы. В то же время имеются такие термические и калорические величины, которые при одних фазовых переходах терпят разрыв, при других — непрерывны. Поэтому различают прерывные и непрерывные фазовые переходы. Прерывные превращения называются фазовыми переходами первого рода. При этих переходах скачком изменяется удельный объем (плотность) вещества (см. например рис. 1.4) и поглощается (или выделяется) теплота. К фазовым переходам первого рода относятся плавление, кристаллизация, кипение и т. д.
Рис. 6.1. Диаграмма фазовых состояний. Сплошные линии — пресная вода, пунктирные — морская вода с соленостью 35 епс
Непрерывные фазовые переходы называются фазовыми переходами второго рода. При этих переходах скачком изменяются теплоемкость при постоянном давлении, сжимаемость, коэффициент теплового расширения и т. д.
Найдем уравнение, характеризующее фазовые переходы первого рода. Для этого воспользуемся условием равенства химических потенциалов при равновесии двух фаз (6.11). Дифференцируя (6.11), получим:
Производные, входящие в это выражение найдем, используя уравнения Гиббса-Дюгема (2.48) для одной частицы, которое выглядит таким образом:

где г) и V — энтропия и объем одной частицы. Уравнение (6.15) является дифференциальным уравнением кривой равновесия и называется уравнением Клапейрона-Клаузиуса. При изобарических процессах уравнение (6.15) можно выразить через разность энтальпий, если воспользоваться выражением (2.33):
Чаще уравнение (6.15) записывают в виде:
где Х = 7’ (г)»-г|’) — скрытая теплота перехода (теплота испарения, сублимации, плавления) на грамм (моль) вещества. При изобарических процессах — Х = Н» — Н’. Отсюда видно, что при переходе вещества, например, воды из фазового состояния с большей энтальпией в фазовое состояние с меньшей происходит отдача излишков энтальпии, а при обратном переходе необходимое количество энтальпии поступает из-за пределов термодинамической системы. Величина А. называется «скрытой» теплотой потому, что при переходе, например, жидкости в пар это тепло от жидкости «отнимается», но не происходит одновременного непосредственного нагрева окружающей воздушной среды. Нагрев может происходить только при обратном фазовом переходе — конденсации водяного пара, и этот процесс может происходить в другое время и в другом месте.
Как видно из (6.16), уравнение Клапейрона-Клаузиуса связывает между собой теплоту перехода, изменение (скачок) объема и наклон кривой равновесия в точке перехода. Основное применение уравнения (6.16) состоит в вычислении удельных теплот испарения, плавления, сублимации.
Уравнение Клапейрона-Клаузиуса вида
используется для вычисления изменения температуры фазового перехода (например, температуры замерзания).
Ранее условия равновесия описывались нами без учета поверхностных явлений. Теперь включим в рассмотрение эти процессы.
🔍 Видео
Фазовые равновесия | ФизхимияСкачать
Лекция №5 "Фазовые переходы" (Попов П.В.)Скачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Румянцева М.Н.- Общая и неорганическая химия. Лекции - 4.Фазовые равновесияСкачать

Уравнение КЛАПЕЙРОНА-КЛАЗИУСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать

Физический кружок: реальные газы, фазовое равновесие | Шестое занятиеСкачать

ФАЗОВЫЕ переходы II рода. Газ ВАН-ДЕР-ВААЛЬСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Уравнения состояния. Фазовое равновесиеСкачать

Термодинамика Л4.1. Фазовые переходыСкачать

Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Караваев В. А. - Молекулярная физика - Термодинамический потенциал. Фазовые переходыСкачать
Фазовые переходы IIого родаСкачать