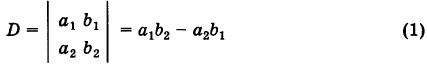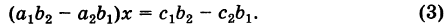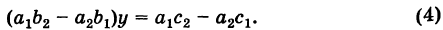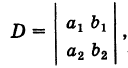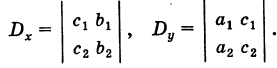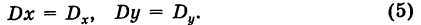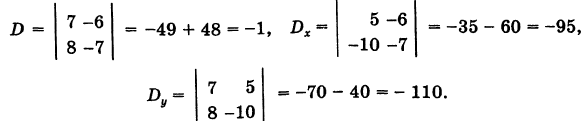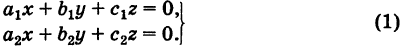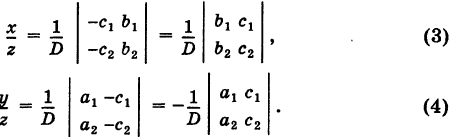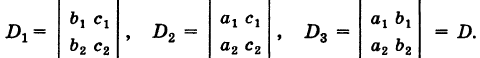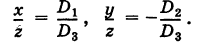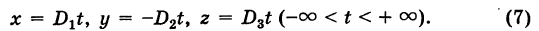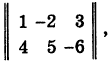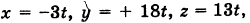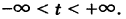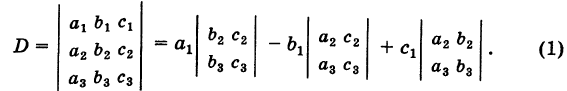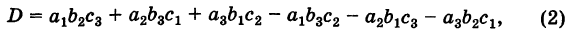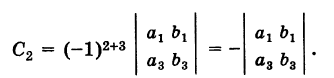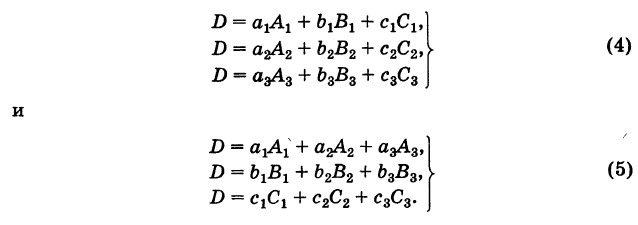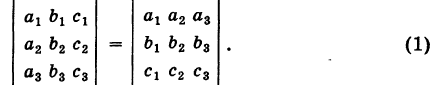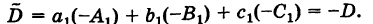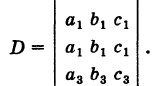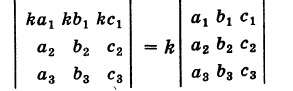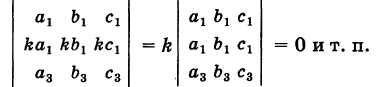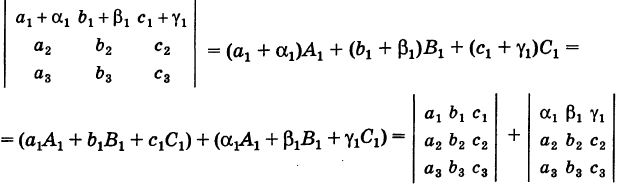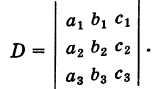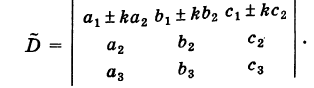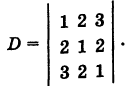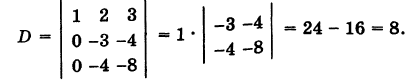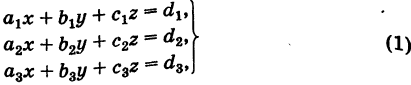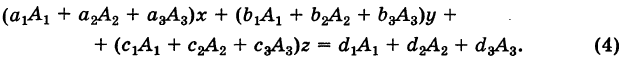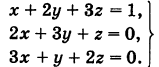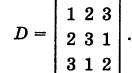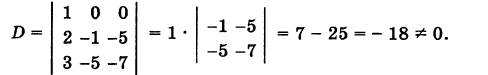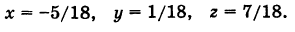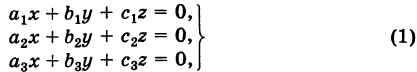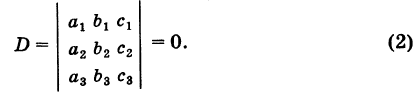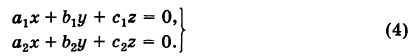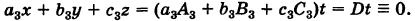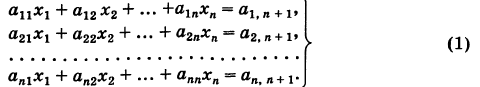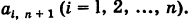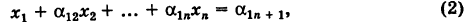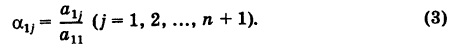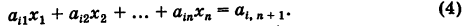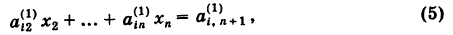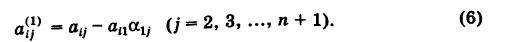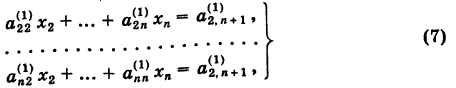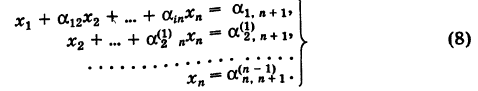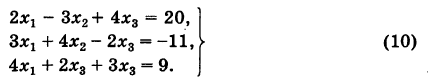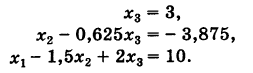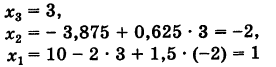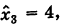| Название: Определители Решение систем линейных уравнений Раздел: Рефераты по математике Тип: реферат Добавлен 16:12:19 19 мая 2010 Похожие работы Просмотров: 219 Комментариев: 21 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Формулы ( 6 ) – это формулы Крамера.
ЗАМЕЧАНИЕ. Г. Крамер (1704 – 1752) – швейцарский математик.
Заметим, что теорема Крамера применима, когда число уравнений равно числу неизвестных и когда определитель системы D отличен от нуля.
Если определитель системы равен нулю, то в этом случае система может либо не иметь решений, либо иметь бесчисленное множество решений. Эти случаи исследуются особо, с ними можно подробно познакомиться в рекомендуемой литературе.
Отметим только один случай:
Если определитель системы равен нулю (D = 0), а хотя бы один из дополнительных определителей отличен от нуля, то система решений не имеет (т.е. является несовместной).
Теорему Крамера можно обобщать для системы n линейных уравнений с n неизвестными.
Если 
формулам Крамера:
Дополнительный определитель 
xi заменить столбцом свободных членов.
Заметим, что определители D, D1 , … , Dn имеют порядок n .
На лекции рассмотрена новое понятие – определитель, подробно рассмотрены определители второго и третьего порядков, часто встречающиеся на практике. Для определителя третьего порядка приводятся два способа вычисления. Рассмотрена теорема Крамера, которая дает практический способ решения систем линейных уравнений, для случая, когда решение единственное. Более подробно с этой темой можно познакомиться в рекомендуемой литературе.
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Применение определителей к исследованию и решению системы линейных уравнений.
Рассмотрим систему n линейных уравнений с n неизвестными:
1) Если определитель системы
 |  |
то система имеет единственное решение, определяемое формулами Крамера:
хi = 
где Δ хi – определитель, полученный из Δ заменой элементов i столбца на столбец свободных членов.
2) Если Δ = 0, а среди определителей Δ хi есть не равные нулю, то система не имеет решения.
3) Если Δ = Δ х1=Δ х2=. . .=Δ хk = 0 , причем один из миноров (п – 1) –го порядка определителя Δ не равен нулю. Тогда система сводится к п – 1 уравнениям; в этом случае одно из уравнений есть следствие остальных. Одному из неизвестных можно дать произвольное значение. Остальные неизвестные определяются единственным образом из системы п – 1 уравнений.
Пример 1: Решить систему уравнений:
Здесь Δ = 7; Δх = 14; Δу = — 7.
Δ ≠ 0, следовательно система имеет единственное решение, определяемое формулами Крамера:
хi = 
Тогда х = 

Пример 2: Решить систему уравнений:
Здесь Δ = 11, Δх = 11,Δу = 55 ,Δz = -22.
Δ ≠ 0, следовательно система имеет единственное решение, определяемое формулами Крамера:
хi = 
Тогда х = 


Пример 3: Решить систему уравнений:
Здесь Δ = Δ х1=Δ х2=. . .=Δ хk = 0.
Вычеркнув четвертую строку и четвертый столбец, получим минор


Система сводится к трем уравнениям:

Четвертое уравнение есть их следствие. Неизвестному х4 можно дать любое значение. Из последней системы находим:
х1 = 

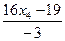
Ответ: <(х1, х2, х3, х4)| х4 


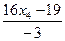
127. Решить систему уравнений методом последовательного исключения неизвестных:
| a) -3х1 + 2х2 – 4х3 + х4 = -7, -5х1 – 3х3 + 2х4 = -6, х1 – 3х2 – х3 + 4х4 = 7, 2х1 + 5х2 + 3х4 = 0; | b) 5х1 — 3х2 + 7х3 + х4 = 5, х1 + х2 – 5х3 + 3х4 = -7, 3х1 — х2 + х3 + 2х4 = 1, 2х1 – 3х3 + х4 = 2. |
128. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1– 5х2 + х3 – 3х4 = -4, -4х1 + 2х2 + 3х3 + х4 = 5, 2х1 + х2 – 4х4 = 8, —х1 + 6х2 – 2х3 + х4 = 6; | b) 2х1– х2 + х3 – 2х4 = -3, 3х1 + 2х2 – х3 – 4х4 = -7, х1 – 3х2 + 2х4 = -2, -2х1 + 3х3 – х4 = 7. |
129. Решить систему уравнений методом последовательного исключения неизвестных:
| а) -2х1– х2 + 3х3 – х4 = 0, 3х1 – 4х3 + 2х4 = 4, х1 + 3х2+2х3 – х4 = 5, -4х1 – 5х2 + х3 +3х4 = -2; | b) 2х1– х2 – 3х3 + х4 = 0, —х1 + 5х2 + х3 + 2х4 = 12, х1 + 4х2 – 2х3 + 3х4 = 3, 3х1 + х3 – 5х4 = 0. |
130. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1– 2х2 + 3х3 – 4х4 = 6, 2х1 + х2 – 4х3 – 3х4 = 2, 3х1 + 4х2 – х3 + 2х4 = 8, -4х1 – 3х2 + 2х3 +х4 = 2; | b) х1+ 5х2 – 2х3 + 3х4 = -1, —х1 + 4х2 + 3х3 + 2х4 = -8, х1 – 7х3 – 3х4 = 2, 3х1 – 2х2 + х3 – х4 = 4. |
131. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1+ 3х2 – 5х3 – 2х4 = -10, 2х1 – х2 + 3х3 + х4 = -2, х1 + 2х2 – 2х3 – х4 = -6, х2 – 2х3 + 3х4 = 1; | b) 2х1– 3х2 + х3 – 4х4 = 9, —х1 – 2х2 + 3х3 + х4 = 8, 3х1 – х2 + 2х3 – 2х4 = 11, х1 + 4х2 – х3 + 3х4 = -6. |
132. Решить систему уравнений методом последовательного исключения неизвестных:
| а) 3х1– х2 + 2х3 + х4 = 1, 2х1 + 3х2 + 4х3 – 2х4 = 3, х1 + 5х2 + 3х3 – х4 = 4, — х1 – 2х3 + 3х4 = 2; | b) -2х1+ 4х2 – 3х3 + 5х4 = -5, 3х1 – 2х2 + х3 – 4х4 = 8, 4х1 + х2 – 2х3 + 3х4 = 6, -5х1 – 3х2 – х4 = 6. |
133. Решить систему уравнений:
 а) -3х + 2у = -1, а) -3х + 2у = -1, | b 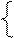 ) — 7х – 12 у = -2, ) — 7х – 12 у = -2, |
| -5х + 4у = -5; | 5х + 3 у = 7. |
134. Решить систему уравнений:
 а) х + 2 у = 3, а) х + 2 у = 3, |  b) 9х + 2 у = 6, b) 9х + 2 у = 6, |
| -3х — 13 у = 5; | -5х + у = 3. |
135. Решить систему уравнений:
 а) — 7х + 2 у = 5, а) — 7х + 2 у = 5, |  b) 13х – 3 у = 1, b) 13х – 3 у = 1, |
| 8х – у = 2; | -7х + 5 у = -13. |
136. Решить систему уравнений:
| а) х + 2у – 4z = 7, | b) -3х +у – 5z = 1, |
| 2х + у – 3z = -5, | х + 7у – 3z = -5, |
| 3х – 3у – z = -6; | 4х – 2у – z = -9. |
137. Решить систему уравнений:
| а) -3х + 2у – 4z = 15, | b) — х – 2у + 4z = 3, |
| -5х + у – 3z = 4, | 6х + 5у – 3z = -18, |
| х – 3у – z = 16; | х + 3у – 7z = 3. |
138. Решить систему уравнений:
| а) 8х + у – 4 z = -3, | b) х + 6у – 7z = 4, |
| 5х + 4у – z = 0, | 11х + у – 6z = -9, |
| х + 3у – 2z = 4; | —2х – 5у + z = -13. |
139. Решить систему уравнений:
| а) х1– х2 + 3х3 – х4 = 6, 3х1 – 2х3 + 2х4 = 4, х1 + 3х2+2х3 – х4 = 1, — х1 – 5х2 + х3 +3х4 = 4; | b) 2х1– х2 – 3х3 + х4 = -13, —х1 + 5х2 + х3 – 8х4 = 5, х1 + 4х2 – 2х3 + 5х4 = -8, 3х1 + х3 – 5х4 = -3. |
140. Решить систему уравнений:
| а) 5х1+ х2 – 2х3 – 9х4 = 9, 3х1 – х3 + 7х4 = 5, -2х1 + 3х2 + х3 + 2х4 = -4, -4х1 + х2 – 2х3 + 5х4 = 0; | b) х1– 2х2 – х3 + 5х4 = 12, -2х1 + 3х2 + 6х3 + х4 = -6, х1 – 7х2 + 2х3 + х4 = 1, 3х1 + х2 – 2х4 = -1. |
Глава 3. Теория пределов
§1.Предел функции
Определение предела функции
Число b называется пределом функции у = f(x) при х → + 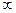
│f(x) – b│ 
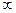


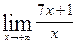
Число b называется пределом функции у = f(x) при х →х0, если, каково бы ни было положительное число ε, можно найти такие числа M и N (N 4 = 81;


Замечая, что 

Пример 2. Найти 
Нахождение предела этой дроби сводится к раскрытию неопределенности 


Разделим числитель и знаменатель дроби на х – 4. Это сокращение допустимо, так как при разыскании предела рассматриваются значения х ≠ 4. Итак, для всех значений х ≠ 4 имеет место тождество 





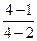
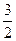
Пример 3. Найти 
В этом случае имеет место неопределенность вида 


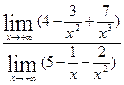
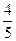
Видео:Решение системы уравнений методом Крамера.Скачать

Определители второго и третьего порядков и их свойства с примерами решения
Содержание:
Определители второго порядка:
Под определителем (детерминантом) второго порядка понимается выражение
Числа
Формула (1) дает правило «развертывания» определителя второго порядка, а именно: определитель второго порядка равен разности произведений его элементов первой и второй диагоналей.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Определители второго порядка
С помощью определителей второго порядка удобно решать линейные системы двух уравнений с двумя неизвестными:
Такую линейную систему, в которой свободные члены находятся в правых частях, для определенности мы будем называть стандартной.
Под решением системы (2) понимается всякая пара чисел (х, у), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным. Аналогично вводится понятие решения для системы, содержащей п неизвестных 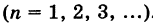
Для нахождения решений системы (2) применим метод исключения. Умножая первое уравнение системы (2) на 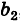
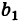
Аналогично, умножая первое уравнение системы (2) на а2 второе — на 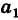
Введем определитель системы
а также дополнительные определители
Заметим, что дополнительные определители Dx и Dy получаются из определителя системы D путем замены коэффициентов при указанном неизвестном на соответствующие свободные члены.
Уравнения (3) и (4) принимают вид
Если 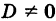
Замечание. Если определитель D = 0, то система (2) или не имеет решений (т. е. несовместна), или имеет бесконечно много решений (т. е. система неопределенная).
Пример:
Решение:
Имеем
Отсюда на основании формул Крамера (6) получаем
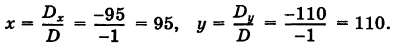
Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Система двух однородных уравнений с тремя неизвестными
Рассмотрим однородную систему
Эта система всегда совместна, так как, очевидно, имеет нулевое решение х = 0, у = 0, z = 0. Однако интересно найти не н у л е в ы е решения (х, у, z) системы (1). Пусть, например, 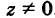
Тогда систему (1) можно переписать в виде
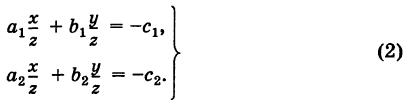
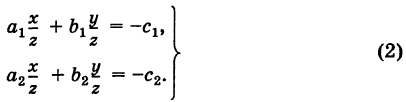
Введем в рассмотрение матрицу коэффициентов системы (1)
Определители второго порядка 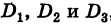
Используя эти обозначения, уравнения (3) и (4) можно переписать в следующем виде:
Равенства (6), очевидно, справедливы также и для нулевого решения.
Таким образом, имеем следующее правило: неизвестные однородной системы (1) пропорциональны соответствующим минорам ее матрицы коэффициентов, взятым с надлежащими знаками.
Обозначая через t коэффициент пропорциональности для отношений (6), получим полную систему решений системы (1):
При выводе формул (7) мы предполагали, что 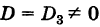
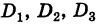
Замечание. Если все миноры 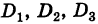
Пример:
Решение:
Составляя матрицу коэффициентов
находим ее миноры: 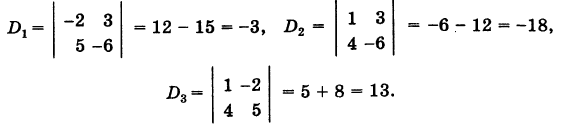
где
Простейшее ненулевое решение системы (1), получающееся при t — 1, есть х = -3, у = 18, z = 13.
Видео:Матричный метод решения систем уравненийСкачать

Определители третьего порядка
Числа 
Раскрывая определители второго порядка (миноры) в формуле (1) и собирая члены с одинаковыми знаками, получаем, что определитель третьего порядка представляет собой знакопеременную сумму шести слагаемых:
из которых три берутся со знаком плюс, а три — со знаком минус.
Пример:
Решение:
Используя формулу (1), имеем 
Определение: Под минором элемента определителя третьего порядка понимается определитель младшего (второго) порядка, получающийся из данного определителя в результате вычеркивания строки и столбца, содержащих данный элемент.
Например, для определителя (3) минором его элемента 2, стоящего во второй строке и в первом столбце, является определитель 
Определение: Алгебраическим дополнением (минором со знаком) элемента определителя третьего порядка называется минор этого элемента, взятый со знаком плюс, если элемент занимает четное место у и со знаком минус, если его место нечетное.
Таким образом, если М есть минор элемента определителя, a i и j — соответственно номер строки и номер столбца, на пересечении которых находится данный элемент, то его алгебраическое дополнение есть
Например, для элемента с2 определителя (1), находящегося во второй строке и в третьем столбце, его алгебраическое дополнение есть
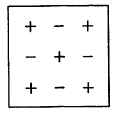
Соответствующие знаки, приписываемые при этом минорам элементов определителя, можно задать таблицей
В дальнейшем алгебраические дополнения элементов определителя с буквенными элементами условимся обозначать соответствующими прописными (большими) буквами.
Теорема Разложения: Определитель третьего порядка равен сумме парных произведений элементов какого-либо ряда его на их алгебраические дополнения (под рядом понимается строка или столбец).
Таким образом, для определителя (1) справедливы шесть разложений:
Легко проверить, что формулы (4) и (5) дают одно и то же выражение (2), принятое за определение.
Замечание. С помощью формул типа (4) или (5), по индукции, можно ввести определители высших порядков.
Видео:10. Метод Крамера решения систем линейных уравнений.Скачать

Основные свойства определителей
При формулировках мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка.
I. (Равноправность строк и столбцов.) Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, т. е.
Действительно, разлагая первый определитель по элементам первой строки, а второй — по элементам первого столбца, в силу теоремы разложения мы получим один и тот же результат.
II. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на обратный.
Пусть, например, в определителе 
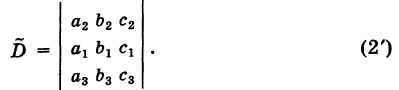
Аналогичное положение получается и в других случаях.
Следствие 1. Определитель, у которого два параллельных ряда одинаковы, равен нулю.
В самом деле, пусть, например,
Переставляя первую и вторую строки определителя, в силу теоремы получим определитель -D. Но очевидно, эта операция не изменяет определитель D, поэтому -D = D и, следовательно, D = 0.
Следствие 2. Сумма парных произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю, т. е. для определителя (2) имеем 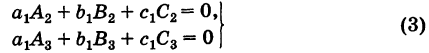
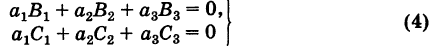
Левые части всех соотношений (3) и (4) представляют собой разложения соответствующих определителей третьего порядка, содержащих два одинаковых параллельных ряда и, следовательно, равны нулю. Например, 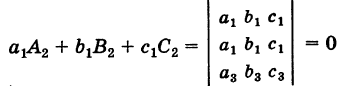
III. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя, т. е.
Это свойство непосредственно вытекает из разложения определителя по элементам соответствующего ряда.
Следствие 1. Если все элементы какого-либо ряда определителя равны нулю, то определитель равен нулю.
Следствие 2. Если элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда его, то определитель равен нулю.
Например, имеем
IV. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Следствие. Величина определителя не изменится, если /с элементам какого-либо ряда его прибавить (или отнять) числа, пропорциональные соответствующим элементам параллельного ряда с одним и тем же коэффициентом пропорциональности (так называемые «элементарные преобразования определителя»).
Рассмотрим, например, определители
Используя свойства IV и III, будем иметь 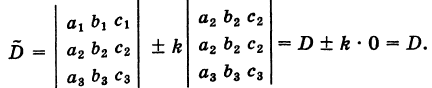
Пример:
Вычислить симметричный определитель
Решение:
Вычитая из второй строки удвоенную первую строку, а из третьей строки утроенную первую строку, получим
Система трех линейных уравнений
Рассмотрим стандартную линейную систему трех уравнений
свободные члены которых находятся в правых частях. Под решением системы понимается всякая тройка чисел (х, у, г), удовлетворяющая этой системе. Введем определитель системы
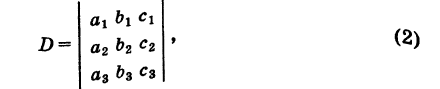
Последовательно умножая уравнения системы (1) на алгебраические дополнения 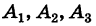
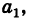
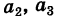
Отсюда, применяя теорему разложения и следствие 2 к свойству II, будем иметь 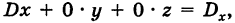

Если определитель системы 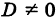
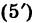
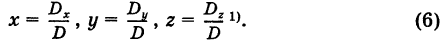
Замечание. Если определитель системы D = 0, то система (1) или несовместна, или имеет бесконечно много решений.
Пример:
Решение:
Вычитая из второго столбца удвоенный первый столбец, а из третьего столбца утроенный первый столбец, получим
Для дополнительных определителей находим следующие значения: 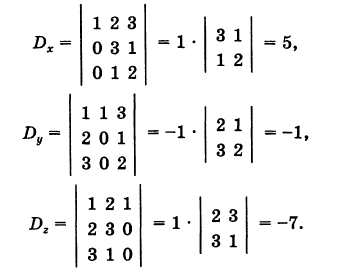
Однородная система трех линейных уравнений
Рассмотрим линейную систему
свободные члены которой равны нулю. Такая линейная система называется однородной.
Однородная линейная система (1), очевидно, допускает нулевое решение х = 0, у = 0, z = 0 и, следовательно, всегда совместна.
Интересно выяснить случаи, когда однородная система имеет ненулевые решения.
Теорема: Линейная однородная система трех линейных уравнений с тремя неизвестными имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т. е.
Доказательство: Пусть система (1) имеет ненулевое решение 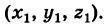
Пусть D = 0. Тогда линейная система (1) либо несовместна, либо имеет бесконечно много решений. Но наша система совместна, так как имеется нулевое решение. Следовательно, система (1) допускает бесконечно много решений, в том числе и ненулевые.
Замечание. Укажем способ нахождения ненулевых решений однородной системы (1) в типичном случае.
Пусть определитель системы D = 0, но не все его миноры второго порядка равны нулю.
Мы будем предполагать, что
(этого всегда можно добиться с помощью перестановки уравнений и изменения нумерации неизвестных).
Рассмотрим подсистему, состоящую из двух первых уравнений системы (1):
В силу решения этой системы имеют вид
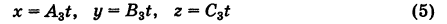
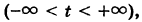
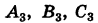
Следовательно, формулы (5), где t произвольно, дают все решения полной системы (1).
Геометрически уравнения системы (1) представляют собой уравнения трех плоскостей в пространстве Oxyz. Если определитель 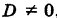
Система линейных уравнений с многими неизвестными. Метод Гаусса
Рассмотрим систему 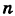
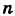
Здесь для коэффициентов системы введена двойная индексация, а именно: у коэффициента 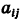
Наиболее простой метод решения системы (1) — это метод исключения. Мы изложим его в форме схемы Гаусса (обычно называемой методом Гаусса).
Пусть для определенности 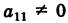
Рассмотрим i-e уравнение системы (1):
Для исключения xx из этого уравнения умножим приведенное уравнение (2) на ап и полученное уравнение вычтем из уравнения (4). Тогда будем иметь
Таким образом, получаем укороченную систему
коэффициенты которой определяются по формулам (6).
Если ее ведущий коэффициент 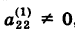
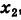
Для определения неизвестных 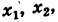
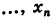
Отсюда последовательно находим неизвестные (обратный ход) 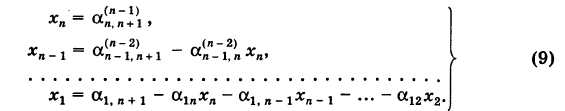
Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.
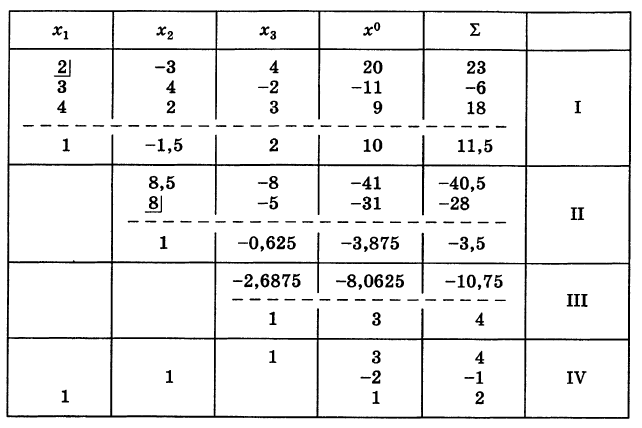
Пример:
Методом Гаусса решить систему
Решение:
Составляем таблицу коэффициентов системы (10), рассматривая свободные члены ее как коэффициенты при 
Последний столбец 
Считая отмеченный коэффициент 2 ведущим и деля на этот коэффициент все элементы первой строки таблицы (включая и входящий в столбец 
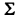
Далее, используя формулу (6), подсчитываем коэффициенты укороченной системы, не содержащей неизвестного xv Для наглядности будем называть строку, содержащую коэффициенты приведенного уравнения, приведенной, а столбец, содержащий ведущий элемент раздела, — ведущим. Тогда на основании формулы (6) справедливо правило: преобразованные коэффициенты схемы Гаусса, равны ее прежним коэффициентам минус произведение «проекций» их на соответствующие приведенную строку и ведущий столбец таблицы. Пользуясь этим, заполняем раздел II таблицы, включая контрольный столбец. Для удобства вычислении в качестве ведущего коэффициента раздела П берем элемент 8 (см. табл.).
Аналогично производится заполнение раздела III таблицы. Этим заканчивается прямой ход схемы Гаусса.
Неизвестные 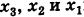
(обратный ход). Результаты обратного хода помещены в разделе IV таблицы.
Заметим, что если в качестве свободных членов взять элементы столбца 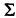
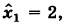
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Свойства определителя - bezbotvyСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

5 способов вычисления определителя ★ Какой способ лучше?Скачать

Решение системы уравнений методом ГауссаСкачать

Решение системы трех уравнений по формулам КрамераСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать
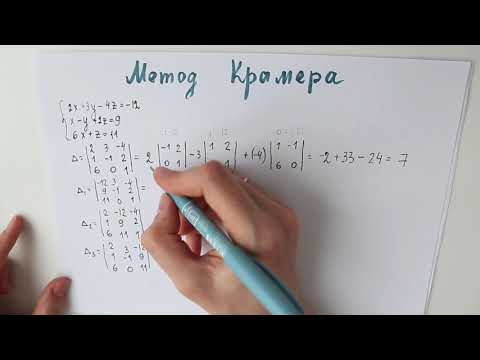
Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение системы уравнений методом Крамера 4x4Скачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Решение систем линейных уравнений с помощью матрицСкачать



 (1)
(1)


 » + » » – «
» + » » – « 

 .
. .
. .
.
 .
. .
.
 .
. .
. .
.


 .
.
 .
.

 (3)
(3) .
. D2 =
D2 =  .
. (4)
(4)

 .
. (5)
(5)
 .
.