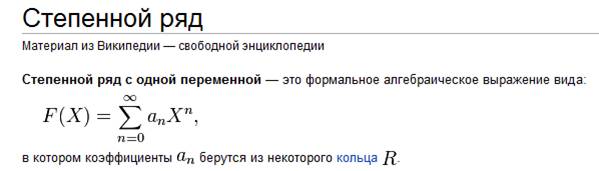
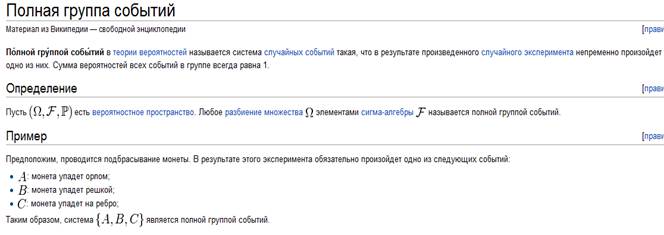
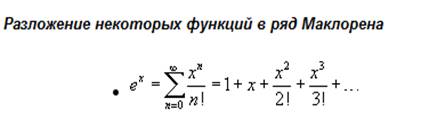Применение степенных рядов к решению дифференциальных уравнений к вычислению интегралов (3 видео)

52. Решение дифференциальных уравнений с помощью сТепенных рядов

С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

Рассмотрим линейное дифференциальное уравнение вида:

Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

Это решение можно представить степенным рядом:

Для нахождения решения остается определить неизвестные постоянные Ci.

Эта задача решается Методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

Затем приравниваем коэффициенты при одинаковых степенях Х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты Ci.

Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.

Пример. Найти решение уравнения C начальными условиями Y(0)=1, Y’(0)=0.

Решение уравнения будем искать в виде

Подставляем полученные выражения в исходное уравнение:

Отсюда получаем:

Получаем, подставив начальные условия в выражения для искомой функции и ее первой производной:

Окончательно получим:

Итого:

Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название Метод последовательного дифференцирования.

Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

Если заданные начальные условия Y(0)=1, Y’(0)=0 подставить в исходное дифференциальное уравнение, получим, что

Далее запишем дифференциальное уравнение в виде и будем последовательно дифференцировать его по Х.

После подстановки полученных значений получаем:

Видео:Применение степенных рядов к решению дифференциальных уравнений.Скачать

Применение степенных рядов к решению дифференциальных уравнений к вычислению интегралов

Сходящиеся степенные ряды имеют разнообразные приложения. С их помощью вычисляют приближенные значения функций, пределы некоторых функций и «неберущиеся» или сложные для вычисления интегралы с заданной точностью, а также интегрируют дифференциальные уравнения.

1. Приближенное вычисление значений функций

Пусть требуется вычислить значение функции f ( x ) при x = x ₀ с заданной точностью ε>0. Предположим, что для функции в окрестности точки x ₀ имеет место теорема 3.27, то есть применима формула Тейлора (3.52) главы III с остаточным членом (3.54) в форме Лагранжа. При x ₀ = 0 получим ряд Маклорена, обозначенный ранее формулой (3.55):

Примечание. Может оказаться, что ряд Маклорена, составленный для функции f ( x ), либо расходится, либо сходится не к функции f ( x ). Говорят, что такая функция в ряд Маклорена не раскладывается

Вспомним разложения по формуле Маклорена некоторых элементарных функций, обозначенных в главе III (3.57) – (3.61), на основе которых приведём соответствующие разложения в степенной ряд:

областью сходимости рядов (9.15), (9.16), (9.17) является вся числовая прямая (–∞;+∞) ;

После выяснения сходимости на концах интервала областью сходимости ряда (9.18) является полуинтервал (–1;1].

с интервалом сходимости (–1;1) ; на концах интервала при x =± 1 сходимость ряда зависит от конкретных значений m .

Пример 9.9. Найти sin 28 0 с точностью до 0,0001.

Решение . Переведем 28 0 в действительное число. Составим пропорцию . Отсюда получим . Согласно формуле (9.15)

Полученный знакочередующийся ряд удовлетворяет условиям теоремы 9.8 Лейбница. Так как четвертый член ряда меньше заданной точности 0,0000013 sin 28 0 с точностью до 0,0001 достаточно первых трех членов ряда. Окончательно получаем .

Значение sin 28 0 , вычисленное с помощью калькулятора равно 0,46923, найденное по таблице Брадиса равно 0,4695

Примечание . В случаях знакопеременных или знакоположительных рядов составляют ряд из абсолютных величин членов и стараются подобрать положительный ряд с большими членами (часто таким рядом является сходящийся ряд геометрической прогрессии), который легко бы суммировался. В качестве оценки погрешности берут величину остатка этого нового ряда

2. Приближенное вычисление пределов функций

Применение степенных рядов к приближенному вычислению пределов различных функций является либо альтернативным методом решения, либо позволяет найти пределы, другими способами не вычисляемые. Чтобы проиллюстрировать последний случай, рассмотрим пример.

Пример 9.10. Найти предел функции .

Решение. В главе III нами были рассмотрены различные способы вычисления пределов функций с помощью замечательных пределов (пункт III.2) и теоремы 3.21 Лопиталя (пункт III.5). Однако для нахождения заданного предела данные методы решения не применимы, так как функция под пределом содержит одновременно экспоненциальную и тригонометрические функции, а в процессе дифференцирования по правилу Лопиталя числитель и знаменатель дроби усложняются.

Вычислим заданный предел путем разложения в степенные ряды все функции, содержащиеся под пределом. При этом возьмем столько членов разложений, чтобы наибольшая степень переменной равнялась четырем, так как x → 0 и x 4 дает точность вычислений не менее 0,0001.

После применения формул (9.15)-(9.17) получим:

3. Приближенное вычисление определенных интегралов

Пусть требуется вычислить с точностью до ε>0. Для приближенного вычисления неопределенных и определенных интегралов в тех случаях, когда первообразная не выражается в конечном виде через элементарные функции либо нахождение первообразной сложно или трудеёмко, также применяются сходящиеся бесконечные ряды.

Если подынтегральную функцию f ( x ) можно разложить в ряд по степеням x и интервал сходимости (– R ; R ) включает в себя отрезок [ a ; b ], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяются так же, как и при вычислении значений функций.

Пример 9.11. Вычислить , с точностью до 0,001.

Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив в разложении (9.15) функции sin x аргумент x на , имеем:

Полученный ряд сходится абсолютно по теореме 9.8 (проверить самостоятельно). Так как четвертый его член по абсолютной величине 0,00011

Пример 9.12. Вычислить интеграл при с точностью до 0,0001.

Решение . Разложим по (9.17) подынтегральную функцию в ряд Маклорена, заменяя x на (– x 3 ):

На отрезке проинтегрируем данное равенство:

Получили знакочередующийся ряд, сходящийся по признаку Лейбница (теорема 9.8). Так как требуемая точность вычислений составляет 0,0001 и четвертый член ряда по модулю 0,000016 меньше 0,0001, то достаточно сложить первые три слагаемые:

4. Приближенное решение дифференциальных уравнений

В главе III.5 (схема 32) был рассмотрен механический смысл производной функции одной переменной. Если уравнение траектории движения материальной точки описывается уравнением y = f ( x ), то скорость движения − это , а ускорение − . Ряд задач, встречающихся на практике, описывают движение некой механической системы уравнениями, которые одновременно содержат все эти три характеристики − , то есть приводят к обыкновенным дифференциальным уравнениям.

Если способ решения дифференциального уравнения слишком сложен или искомое решение не выражается через элементарные функции в конечном виде, то для приближенного решения уравнения можно воспользоваться рядом (3.52) Тейлора. Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.

Пусть, необходимо решить уравнение второго порядка

4.1. Метод последовательного дифференцирования ДУ. Будем искать решение y=y(x) уравнения (9.20) в виде ряда Тейлора по степеням x – x ₀ :

Алгоритм решения следующий:

1) первые два коэффициента ряда берем из начальных условий (9.21);

2) третий коэффициент находим из самого уравнения (9.20), подставляя в него начальные условия ;

3) значения последующих коэффициентов , … вычисляем последовательным дифференциро-ванием заданного уравнения (9.20) по x и подстановкой в найденную производную всех полученных до этого значений при x = x ₀ ;

4) процесс дифференцирования продолжаем вплоть до определения членов ряда, количество которых обычно задается условием задачи;

5) найденные значения производных подставляем в разложение (9.22).

Ряд (9.22) представляет собой искомое частное решение уравнения (9.20) для всех значений переменной x, принадлежащих его области сходимости. Частичная сумма этого ряда будет приближенным решением заданного ДУ.

Примечание . Способ последовательного дифференцирования применим для решения дифференциальных уравнений произвольного n -го порядка. В этом случае коэффициенты первых n членов разложения берут из n заданных начальных условий; следующий ( n + 1)-ый коэффициент − из самого уравнения при подстановке в него начальных условий; с ( n + 2)-го члена ряда начинают процесс дифференцирования

Пример 9.13. Методом последовательного дифференцирования найти шесть первых членов (отличных от нуля) разложения в ряд решения уравнения .

Решение . Будем искать решение уравнения в виде степенного рада по степеням x + 1:

По условию y ( – 1)=2 , . Находим , подставив x = –1 в исходное уравнение . Для нахождения последующих коэффициентов дифференцируем заданное по условию уравнение:

Подставляя найденные значения производных в искомый ряд, получаем:

4.2. Метод неопределенных коэффициентов применяется для интегрирования линейных дифференциальных уравнений с переменными коэффициентами вида

Приближенное решение уравнения (9.23) возможно лишь в предположении, что коэффициенты и свободный член f ( x ) разлагаются в ряды по степеням x – x ₀ , сходящиеся в некотором интервале ( x ₀ – R ; x ₀ + R ). Тогда искомое решение y = y ( x ) ищется в виде степенного ряда

с неопределенными коэффициентами, количество членов которого обычно задано по условию.

Приведем краткий алгоритм решения:

1) первый коэффициент находят из уравнения при первом начальном условии y ( x ₀ )= y ₀ = c ₀

2) дифференцируют ряд (9.25)

3) второй коэффициент находят из (9.26) при втором начальном условии , после чего ряд (9.25) принимает вид

4) вычисляют вторую производную , дифференцируя ряд (9.26);

5) подставляют найденные в исходное уравнение, одновременно коэффициенты и свободный член f ( x ) заменяют их разложениями в степенные ряды;

6) раскрывают скобки, приводят подобные слагаемые и сравнивают коэффициенты при одинаковых степенях переменной x ;

7) из полученных уравнений находят неизвестные коэффициенты c_i и подставляют их найденные значения в искомый ряд (9.25).

Построенный ряд (9.25) сходится в том же интервале ( x ₀ – R ; x ₀ + R ) и является приближенным решением заданного уравнения (9.23).

Примечание . Для решения линейных ДУ с переменными коэффициентами произвольного n -го порядка их дифференцирую n раз, то есть столько раз, каков порядок заданного уравнения.

Пример 9.14. Найти первые семь членов разложения в ряд приближенного решения дифференциального уравнения , используя метод неопределенных коэффициентов.

Решение . Будем искать приближенное решение заданного уравнения в виде степенного ряда по степеням переменной x :

с учетом начальных условий

Продифференцируем дважды равенство (9.27):

Коэффициенты заданного уравнения p ₁ ( x )= – x , p ₂ ( x )=1. Разложим его правую часть в степенной ряд:

Подставим производные , функцию (9.27) и правую часть (9.28) в исходное уравнение, получим:

Приравняем коэффициенты при одинаковых степенях переменной в обеих частях последнего равенства:

Найденные значения коэффициентов подставим в разложен ие искомого решения (9.27):

. Очевидно, что приближенным решением заданного уравнения является функция y = cos x

Видео:Частное решение ДУ, с помощью рядаСкачать

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Основные понятия

Определение.Уравнение вида

связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у’, у»,…, у(n) уравнение (*) в тождество.

Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.

Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y’+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида y»+ρy’+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.

Рассмотрим линейное уравнение второго порядка вида:

у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.

называется характеристическим уравнением данного уравнения (1).

Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.

Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:

1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид .

2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид:

u1 , u2 , u3 , . , un , .

— бесконечная числовая последовательность; un называется общим членом ряда.

Определение: Ряд называется сходящимся, если сумма первых его n членов стремится к конечному пределу S, называемому суммой ряда.

Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда.

9,10) Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Особенно часто и эффективно степенные ряды используются для точного и приближенного решения дифференциальных уравнений, обыкновенных и с частными производными. Не вдаваясь в сложные теоретические обоснования, рассмотрим дифференциальное уравнение Бесселя

x2y» + xy’ + (x2 — n2)y = 0,

где n — постоянная (необязательно целая), x — независимая переменная, а y = y(x) — искомая функция. Решения этого уравнения, называемые функциями Бесселя, нашли применение практически во всех областях современного естествознания.

Будем искать y в виде обобщенного степенного ряда

где p, ak — неизвестные постоянные, причем a0 ? 0. Дифференцируя этот ряд дважды под знаком суммы, подставим выражения функции y и ее производных y’, y» в уравнение (7). Затем сделаем приведение подобных членов, и коэффициенты полученного ряда приравняем нулю. После этого получим бесконечную систему уравнений

ak[(p + k)2 — n2] + ak — 2 = 0, k = 2, 3, 4, _,

p = ? n, a1 = a3 = a5 = _ = 0,

В случае нецелого n функции y1(x) и y2(x), соответствующие значениям p = n и p = — n, являются линейно-независимыми и любое другое решение дифференциального уравнения (7) имеет вид y = c1y1(x) + + c2y2(x), где c1 , c2 — постоянные. В случае целого n эти функции отличаются друг от друга только постоянным множителем, поэтому определяют лишь одно из двух линейно-независимых решений дифференциального уравнения.

14)

Дискретной случайной величинойназывается такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.