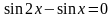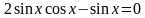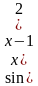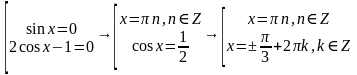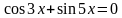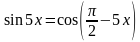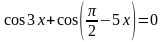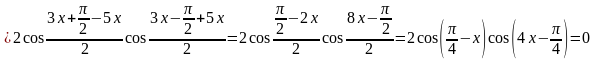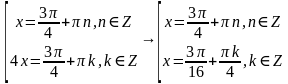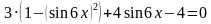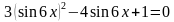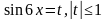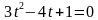Применение основных тригонометрических формул для решения уравнений 10 класс никольский

конспект урока в 10 классе и презентация к нему по теме «решение тригонометрических уравнений с помощью тригонометрических формул». Цели урока: знакомство обучающихся со способами решения тригонометрических уравнений путем преобразования уравнений с помощью основных тригонометрических формул.

Видео:11.3 Применение основных тригонометрических формул для решения уравнений (Алгебра 10 Никольский)Скачать

Скачать:

Видео:Применение тригонометрических формул для решения уравненийСкачать

Предварительный просмотр:

Тема : Применение тригонометрических формул к решению уравнений.

Тип: объяснение нового материала.

Оснащение урока: компьютер, мультимедийный проектор, авторская презентация.

1. повторить формулы корней простейших тригонометрических уравнений;
2. повторить основные тригонометрические формулы;
3. рассмотреть методы решения тригонометрических с применением тригонометрических формул;
4. составить алгоритм решения тригонометрических уравнений с применением основных тригонометрических формул;
5. проконтролировать степень усвоения основных знаний, умений и навыков, полученных на уроке.

I. Организационная часть

1. проверить наличие личного состава;
2. проверить готовность к занятию и внешний вид суворовцев;
3. объявить тему, ход и метод проведения занятия.

II. Проверка выполнения задания на самоподготовку

1. проверить уровень усвоения суворовцами изученного материала;
2. активизировать познавательную деятельность суворовцев;
3. повторение изученного материала;
4. развитие умения суворовцев обобщать и применять ранее полученные знания к решению конкретных задач.

1. Работа суворовцев у доски .

Решите уравнения: а) ; б) ; в) .

Найти координаты точки единичной окружности, соответствующей углу: а) ; б) ; в) ; г) ; д) ; е) ; ж) .

Найдите ошибки в решениях тригонометрических уравнений: а) ; б) ; в) ; г) .

Разложите на множители: а) ; б) ; в) .

III. Из истории тригонометрии

1. развитие познавательной деятельности суворовцев;
2. мотивация изучения данной темы.

– Современный вид тригонометрии придал крупнейший математик XVIII столетия Леонард Эйлер – швейцарец по происхождению, долгие годы работавший в России и являющийся членом Петербургской академии наук. Он ввел известные определения тригонометрических функций, сформулировал и доказал известные вам формулы приведения, выделил классы четных и нечетных функций. Жизнь Л. Эйлера очень интересна. Я советую вам познакомиться с ней по книге Яковлева “Леонард Эйлер”.

IV. Объяснение нового материала.

1. познакомить суворовцев с некоторыми методами решения тригонометрических уравнений;
2. развитие аналитического мышления суворовцев;
3. развитие познавательной деятельности суворовцев;
4. обобщение и систематизация полученных на уроке знаний;
5. применение полученных знаний при самостоятельном выполнении заданий;
6. проверка и самопроверка усвоения знаний полученных на уроке.

А. Эйнштейн говорил так: “Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно”.
Вот мы и займемся уравнениями.

Решение уравнений с применением основного тригонометрического тождества.

Чем схожи и чем различаются уравнения:

Применяя формулу или , преобразуем уравнение или в виде или . Выполнив алгебраические преобразования, получим квадратное уравнение относительно или , которое решается путем замены неизвестного.

в) суворовцы выполняют самостоятельно с последующей проверкой.

Алгоритм решения уравнений с применением основного тригонометрического тождества

1. Замена тригонометрической функции.
2. Алгебраическое преобразование уравнения.
3. Замена переменной.
4. Решение квадратного уравнения.
5. Решение простейших тригонометрических уравнений.

Решение уравнений с применением формул сложения

Левую часть уравнений

легко преобразовать с помощью формул сложения в виде

Решая полученные уравнения способом замены неизвестного, получим корни исходных уравнений.

№ 11.16 (б) Суворовцы решают самостоятельно с последующей проверкой.

№ 11.17 Суворовцы решают самостоятельно с последующей проверкой.

Алгоритм решения тригонометрических уравнений с применением формул сложения

1. Применив формулу сложения, получить простейшее тригонометрическое уравнение.
2. Решить простейшее тригонометрическое уравнение.

1. приобретение суворовцами навыков самостоятельного решения уравнений;
2. проверка и самопроверка полученных на уроке знаний;
3. развитие аналитического и логического мышления суворовцев;
4. самооценка суворовцев уровня усвоения учебного материала.

Проверка самостоятельной работы

Суворовцы проверяют работы друг друга, выставляют оценки: «5» за правильно выполненные все задания, «4» — за три любых уравнения или, «3» — за два первых уравнения, «2» — за один или ни одного примера.

Задание на самоподготовку

1. Закрепление материала, изученного на уроке.
2. Отработка самостоятельного решения уравнений.
3. Развитие логического мышления суворовцев.

1. п.11.3, №№ 11.15( б, г ), 11.16( в, г )
2. повторить формулы корней простейших тригонометрических уравнений

1. Повторить алгоритм решения уравнений с применением основного тригонометрического тождества.
2. Повторить алгоритм решения тригонометрических уравнений с применением формул сложения.
3. Оценить работу суворовцев на уроке.

Видео:Алгебра 10 класс. Применение основных тригонометрических формул при решении уравненийСкачать

Применение основных тригонометрических формул для решения уравнений

Урок №9. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Применение основных тригонометрических формул для решения уравнений»

Тема: Применение основных тригонометрических формул для решения уравнений

Цели: продолжить формирование навыков решения тригонометрических уравнений; научить применять основные тригонометрические формулы при решении.

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Откройте тетради, запишите сегодняшнее число и тему урока. Перейдите по ссылке и посмотрите видеоурок:

Пример 1. Решить уравнение:

Решение. Применим формулу синуса двойного угла 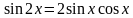, получим:

Вынесем общий множитель за скобку:

Решим распадающееся уравнение, запишем в виде совокупности:

Ответ: ; .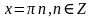

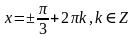
Пример 2. Решить уравнение:

Решение. Используем формулу приведения для 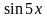, чтобы уравнение было относительно одной функции:

Перепишем уравнение в виде:

Далее применим формулу суммы косинусов, получим:

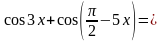
Снова пришли к распадающемуся уравнению, решим его:

Ответ: ; .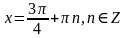

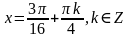
Пример 3. Решить уравнение:

Решение. Применим формулу синуса двойного угла, получим:

Уравнение пока еще зависит от двух функций, поэтому применим к косинусу основное тригонометрическое тождество, получим:

Тогда исходное уравнение примет вид:

Раскроем скобку, приведем подобные и умножим на « -1 »:

Получили квадратное уравнение относительно 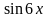. Выполним замену:

Оба значения подходят. Вернемся к замене:

Пример 4. Решить уравнение:

Решение. Применим формулу синуса двойного угла:

Применим основное тригонометрическое тождество:

Перепишем уравнение в виде:

Разделим на , получим:

Введем замену , получим:

Тангенс – функция не ограничена, поэтому оба корня подходят. Вернемся к замене:

ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: выучить теорию, №11.19 (б, г, е).

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Конспект занятия на тему: «Применение основных тригонометрических формул для решения уравнений. Однородные уравнения.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Специальности 08.02.08 «Монтаж и эксплуатация оборудования и систем

газоснабжения », 54.02.01 « Дизайн (по отраслям)», 07.02.01 «Архитектура».

Технологическая карта учебного занятия

Занятие № 3 1 по дисциплине «Математика»

Количество часов __2__

Тема занятия : Применение основных тригонометрических формул для решения уравнений. Однородные уравнения.

Тип занятия : Изучение и первичное закрепление новых знаний и способов деятельности.

Вид занятия: лекция с элементами семинара.

Образовательные – обеспечить повторение и систематизацию материала темы. Научить при решении уравнений применять основные тригонометрические формулы. Создать условия контроля усвоения знаний и умений.

Развивающие – способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.

Оборудование: доска, мел, раздаточный материал.

1. Организационный момент (Запись темы занятия в журнале. Подготовка рабочего места. Создание проблемных ситуаций) (1-5 мин).

2. Проверка знаний обучающихся. Подведение итогов проверки ( ____ мин).

3. Сообщение темы занятия, постановка цели и задач занятия ( ____ мин).

4. Изложение нового материала, применяемая методика ( ____ мин).

При решении тригонометрических уравнений остаются в силе общие правила решения алгебраических уравнений. Если при этом использованы неравносильные преобразования уравнений, то на конечном этапе решения необходимо проверить: принадлежат ли найденные значения неизвестного к корням данного уравнения или нет.

Каждое конкретное уравнение может быть решено различными способами, что при безошибочности выполняемых действий приведет к одному и тому же окончательному результату. Однако следует иметь в виду, что из-за различия методов решения результат может быть получен в разных формах (приводимых друг к другу тождественными преобразованиями).

Тождественные преобразования с помощью тригонометрических формул в процессе решения позволяют, как правило, свести данное уравнение к одному из нескольких основных типов, решаемых стандартными (наиболее часто встречающимися) методами.

Решить уравнение .

Решение. Перенесем слагаемые в одну часть уравнения и по формуле разности синусов имеем

.

Из последнего равенства получается совокупность двух уравнений

, ,

имеющая, соответственно, решения ,

Решение тригонометрических уравнений, сводящихся к квадратным.

При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества:

Пример . Решить уравнение : 2 cos 2 x + 3 sin x = 0.
Решение :

т . к . cos 2 x = 1 — sin 2 x,

2(1 — sin 2 x) — 3 sin x = 0,

2 sin 2 x — 3 sin x — 2 = 0.
sin x = t, t = -1/2, t = 2

si n x =-1/2 или sin x = 2-решений не имеет

х = (-1) k arcsin(-1/2)+πk

x = (-1) k+1 π/6 +πk, k Є Z.

Решение однородных уравнений

Однородными называются уравнения вида a ·sin x + b ·cos x = 0 — первой степени,
a · sinx + b ·sin x ·cos x + c ·cos x = 0 — второй степени и т.д., где a , b , c — числа.
Однородные уравнения любой степени решаются делением на подходящую степень cos x или sin x .

Общий подход к решению однородных уравнений основан на том, что корни уравнений или не являются корнями уравнения (1), так как, если, например, , то из уравнения (1) следует, что и , что противоречит основному тригонометрическому тождеству . Следовательно, левую и правую части уравнения (1) можно разделить на и ввести подстановку

Решение.
Используя основное тригонометрическое тождество , осуществим замену , тогда уравнение (1) примет вид

Введем подстановку , тогда получим квадратное уравнение

Решая его, находим корни . Затем осуществляя обратную подстановку или , получаем решение исходного уравнения.
Ответ:

Решение.
Введем подстановку , тогда уравнение (2) примет вид

откуда . Так как , то корень не подходит. Следовательно,

Ответ:

Решить уравнение

[свериться с ответом]

Ответ:

Решить уравнение

[свериться с ответом]

Ответ:

Решить уравнение

[свериться с ответом]

Ответ:

Решить уравнение

[свериться с ответом]

Ответ:

🎬 Видео

ФОРМУЛЫ ТРИГОНОМЕТРИИСкачать

Решение тригонометрических уравнений. 10 класс.Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

18+ Математика без Ху!ни. Формулы ПриведенияСкачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия. Повторяем основные формулы. Учимся их использовать. Вебинар | МатематикаСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Тригонометрия в ЕГЭ может быть простойСкачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Формулы приведения - как их легко выучить!Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ решение примеров 10 классСкачать