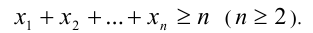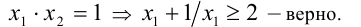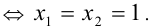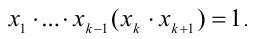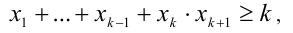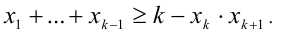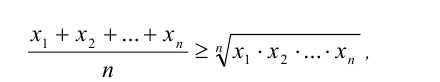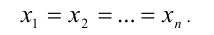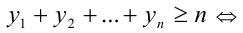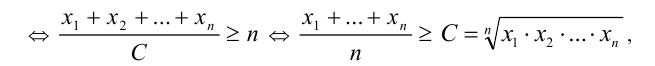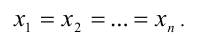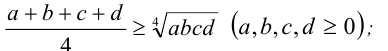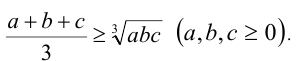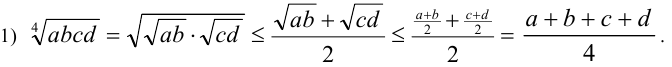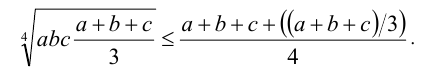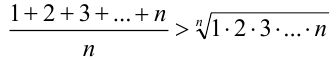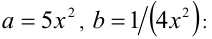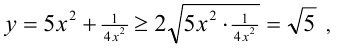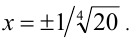Видео:Неравенство Коши — Буняковского | Ботай со мной #049 | Борис Трушин |Скачать
Неравенство Коши
Неравенство Коши
Коши Огюстен Луи (1789—1857) — французский математик, работавший главным образом в области математического анализа (дифференциальные уравнения, теория рядов) и теории функций комплексного переменного. Член Парижской Академии наук. Написал за свою жизнь около 1500 научных работ.
Вначале докажем вспомогательную лемму.
Лемма. Если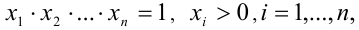 
то
Доказательство. Воспользуемся методом математической индукции. 1) Убедимся в справедливости данного утверждения при n = 2 :
Причём равенство достигается 
2) Предположим, что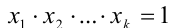 
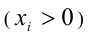
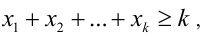
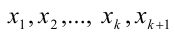
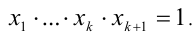
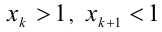
и 
и рассмотрим любые положительные числа 
такие, что 
Если все эти числа равны единице, то доказываемое утверждение очевидно. Пусть это не так. Тогда среди этих чисел найдётся число, меньшее 1, и число, большее 1. Допустим, что 
(можно было наоборот). Имеем равенство:
К этому произведению k чисел применимо предположение индукции, т.е.
откуда получаем 
Но тогда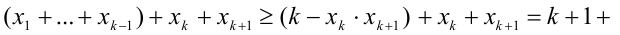 
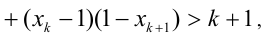
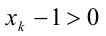
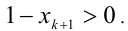
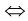
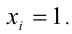
так как 
и 
При этом равенство достигается 
все 
.
3) В силу произвольности k , лемма доказана.
А теперь докажем неравенство между средним арифметическим и средним геометрическим в общем случае (для n чисел).
Теорема (неравенство Коши). Для любых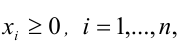 
, справедливо неравенство
которое обращается в равенство тогда и только тогда, когда
Доказательство. Обозначим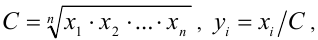 
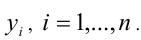
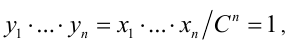
и применим лемму для чисел 
Так как 
то, по доказанному выше, 
причём неравенство обращается в равенство, только когда все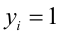 
, т.е.
Пример №131.
Доказать неравенства Коши:
- для четырёх чисел
2) для трёх чисел 
Доказательство. Рассмотрим доказательство указанных неравенств без использования общего неравенства Коши. Докажем вначале неравенство для четырёх чисел, а уже потом с его помощью для трёх чисел.
2) Запишем неравенство Коши для четырёх чисел а,b,c и (а + b + с)/3:
Упростив правую часть, возведём неравенство в четвёртую степень. Сокращая на (а + b + с)/3 и извлекая кубический корень, получим требуемое.
Пример №132.
Сравнить два числа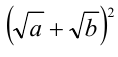 
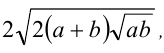
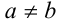
и 
где а и b —неотрицательные числа,
.
Решение:
Преобразуем числа к виду
После деления обоих чисел на 2, приходим к неравенству между средними арифметическим и геометрическим (для чисел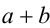 
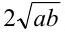
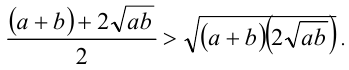
и 
):
Ответ: первое число больше.
Пример №133.
Доказать, что верно неравенство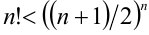 
, где n —любое целое число, большее единицы.
Решение:
Запишем неравенство Коши для чисел 1, 2, 3,…, n :
(знак в неравенстве строгий, так как все числа различны). Упрощая левую часть по формуле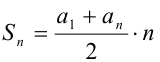 
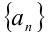
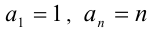
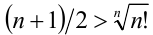
суммы первых n членов арифметической прогрессии 
с первым членом 
, и заменяя справа подкоренное выражение на n!, получим 
, откуда, возводя обе части неравенства в степень n , получаем искомое неравенство доказанным.
Пример №134.
Найти наименьшее значение функции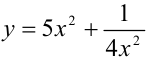
.
Решение:
При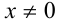 
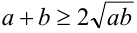
воспользуемся для решения задачи следствием неравенства Коши: 
, положив
причём наименьшее значение функции, равное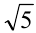 
, достигается тогда и только тогда, когда 
, т.е. при 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Что больше? Или при чем тут неравенство Коши?Скачать
Применение неравенства Коши при решении заданий ЕГЭ
МКУ Управление образования МО «Северо-Байкальский район»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №36» п. Новый Уоян
XV II I межрайонные соревнования юных исследователей
Название исследовательской работы:
Неравенство Коши при решении заданий ЕГЭ
Выполнил: Климов Никита
11 класс МБОУ «СОШ №36» п. Новый Уоян
Консультант: Адериха Анна Петровна
МБОУ «СОШ №36» п. Новый Уоян
Название работы: Неравенство Коши при решении заданий ЕГЭ
поселок Новый Уоян
МБОУ «СОШ №36» 11 класс
Для участия в конференции представлена исследовательская работа «Неравенство Коши при решении заданий ЕГЭ». Эта тема является актуальной, так как предоставляет достаточно богатые возможности при решении различных уравнений, неравенств и других задач. Причем чаще всего применение «классического» неравенства дает «красивое», краткое решение, избавляя учеников от сложных и длинных преобразований, вычислений и на его принципе можно решить разного типа задания ЕГЭ по математике.
Цель работы: раскрыть преимущество способа применения неравенства Коши и изучить область его применения для различных типов заданий ЕГЭ по математике.
Методы исследования : анализ учебной литературы и ресурсов Интернета по данной теме; познавательно — поисковая деятельность; анализ и сравнение данных в поиске материала; анализ полученных результатов.
Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена доказательством неравенства Коши и анализом учебной литературы. Вторая часть – практическая, которая состоит из выбора типов заданий ЕГЭ на применение «замечательного» неравенства, демонстрации этих заданий учащимся 11 класса и отслеживания их уровня усвоения данной темы по технологии В.П.Беспалько.
В заключении делается вывод о том, что если знакомить учащихся с неравенством Коши, вырабатывать у них умения применения данного неравенства, то можно научить учащихся 11–х классов решать различного типа задания ЕГЭ по математике не только стандартными методами.
Название работы: Неравенство Коши при решении заданий ЕГЭ
поселок Новый Уоян
МБОУ «СОШ №36» 11 класс
В школьном курсе математики каждый пятиклассник встречается со средним арифметическим двух или нескольких натуральных чисел ( 
; 
;…). При изучении геометрии каждый школьник знакомится со средним геометрическим двух отрезков ( 
).
Между ними существуют удивительные соотношения, которые исследованы учёными. Огюстен Луи Коши (1789-1857), французский математик, сопоставив две средние величины, пришёл к выводу о том, что среднее арифметическое n чисел всегда не меньше среднего геометрического этих чисел ( 
) . Меня заинтересовал этот факт, и я решил подробно изучить неравенство Коши, рассмотреть применение его к решению задач.
Оказалось, что подробное знакомство с этим неравенством может быть полезно мне не только для расширения кругозора, но также и потому, что на его принципе можно решить разного вида задания ЕГЭ.
Выбранная тема «Неравенство Коши при решении заданий ЕГЭ» является актуальной, так как предоставляет достаточно богатые возможности при решении различных уравнений, неравенств и других задач. Причем чаще всего применение «классического» неравенства дает «красивое», краткое решение, избавляя учеников от сложных и длинных преобразований, вычислений.
Гипотеза исследования заключается в том, что помимо основных методов решения заданий ЕГЭ по математике можно применять неравенство Коши, позволяющее решать задания разных типов.
Объект исследования: задания контрольно — измерительных материалов единого государственного экзамена по математике прошлых лет.
Предметом исследования: организация дополнительного занятия по теме «Неравенство Коши при решении заданий ЕГЭ» для учащихся 11 класса.
Цель работы: раскрыть преимущество способа применения неравенства Коши и изучить область его применения для различных типов заданий ЕГЭ по математике
Достижение цели потребовало решения ряда задач:
проанализировать учебной литературы
показать применение неравенств для решения заданий ЕГЭ;
провести занятие «Неравенство Коши при решении заданий ЕГЭ»
отследить уровень усвоения темы по технологии В.П.Беспалько
Неравенство Коши и его доказательство
Для начала рассмотрим определения среднего арифметического и среднего геометрического величин.
Среднее арифметическое — это сумма всех чисел, делённая на их количество.
Для двух чисел: (где a , b два различных неотрицательных числа); для трех чисел: ; д ля n чисел: 
.
Средним геометрическим для n положительных чисел а 1 , а 2, . а n называется такое положительное число а, что а n = а 1 а 2 … а n , обозначается так: 
.
Задача . Пусть a и b неотрицательные числа. Доказать, что 
(1)
Доказательство . Составим разность левой и правой частей неравенства:
.
В итоге получили неотрицательное число, значит
Равенство левой и правой частей неравенства достигается, только тогда, когда a = b , если a ≠ b , то 
Таким образом, с реднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Это неравенство называют неравенством Коши в честь французского математика Огюстена Луи Коши. Докажем неравенство (1) для нескольких слагаемых.
Для четырех чисел неравенство Коши имеет вид: 
. (2)
Доказательство : 
.
Неравенство (2) станет равенством при a = b , c = d , , то есть при a = b = c = d .
Для трех чисел неравенство Коши имеет вид: 
.
Доказательство : 
, откуда a + b + c ≥ 
.
Равенство в нем достигается при a = b = c .
Следствия из неравенства Коши:
Для любого положительного числа а справедливо неравенство
(3)
Причем равенство получится, если а = 1. Т.е. сумма двух положительных взаимно обратных чисел не меньше двойки, причем равенство достигается, когда оба они равны единице.
Пусть а1, а2, …, а n неотрицательные числа, тогда верно неравенство
. (4)
Неравенство Коши можно записать в следующем виде:
, a 2 + b 2 ≥ 2ab , a 2 + b 2 + c 2 ≥ 3 
.
Анализ учебной литературы
Содержание школьных учебников по алгебре 8-11 классов было рассмотрено для общеобразовательных учреждений и для классов с углубленным изучением математики (Приложение 1).
Анализ учебников таких авторов как Макарычев Ю.Н., Никольский С.М., Виленкин Н.Я., Алимов Ш.А., Колмогоров А.Н., Дорофеев Г.В., показал, что изучение неравенств Коши рассматривается в основном в учебниках для углубленного изучения математики. В учебниках для общеобразовательных учреждений его мало где рассматривают.
Вывод: проанализировав содержание школьных учебников, я пришел к выводу, что тема «Неравенство Коши» в большинстве учебников не рассматривается. В тех же учебниках, где этот материал присутствует, он освещен недостаточно полно, что так же выявляет необходимость на вынесение данной темы на дополнительное занятие по математике.
Вариант дополнительного занятия «Неравенство Коши при решении заданий ЕГЭ» (2ч)
Цель занятия: ввести понятие неравенства Коши и его доказательство, произвести контроль по усвоению знаний и умений.
Задачи: — актуализация знаний и умений учащихся;
— введение понятия неравенства Коши и его доказательства;
— решение заданий ЕГЭ.
— проверить у учащихся уровень применения неравенства Коши при решении заданий ЕГЭ.
Методы: объяснительно-иллюстративный, репродуктивный.
Цель: актуализация знаний и умений (понятие среднее арифметического, среднее геометрического).
Метод: репродуктивный. Прием: фронтальный опрос, работа у доски.
Цель: заинтересовать учащихся в изучении понятия «неравенство Коши». Метод: объяснительно-иллюстративный. Прием: беседа.
Вид мотивации: историческая справка.
Цель: ввести понятие неравенства Коши, изложить доказательство, оформить его письменно.
Метод: объяснительно-иллюстративный. Прием: демонстрация
Этап применения понятия
Цель: применить полученное неравенство к решению задач. Метод: частично-поисковый.
Прием: практическая работа.
На данном этапе учащимся предлагается решить задания ЕГЭ профильного уровня любым известным им способом, а затем демонстрируется применение неравенства Коши к этим заданиям.
Найдите сумму коней уравнения 
(задание 5 ЕГЭ)
Решение: 
— ОДЗ.
, применим следствие (1) неравенства Коши для левой части уравнения: 
Равенство будет только в случае, если
, 
Ответ: -1
2) По периметру участка прямоугольной формы, площадь которого равна 540 м 2 , устанавливается ограда. Для двух противоположных сторон используется металлическая ограда по цене 3 рубля за 1 метр. Для других сторон – деревянная ограда, ее цена 5 рублей за 1 метр. Каковы должны быть размеры участка, чтобы полная стоимость ограды была наименьшей? В ответе укажите эту стоимость. (задание 10)
Решение: Если х – сторона участка, вдоль которой устанавливается металлическая ограда, то стоимость ограды можно выразить функцией:
Найдем наименьшее значение этой функции на промежутке (0;+∞). Применим неравенство Коши
Функция принимает наименьшее значение, если в неравенстве достигается равенство, то есть 
Следовательно, стоимость участка будет наименьшей, если стороны участка будут 18м и 30м. Итого, 900+900=1800 Ответ: 1800
3) Найти наименьшее значение функции 
(задание 12)
Представим заданную функцию в следующем виде:
Применим неравенство Коши к этим пяти положительным слагаемым:
, то есть 
,
Решить уравнение 
. Если уравнение имеет несколько корней, в ответе указать больший (задание 13)
Решение: Из уравнения следует, что 
. Представим уравнение данное в виде равносильного уравнения (делим в столбик): 
Если к левой части уравнения применить неравенство Коши, то получим
Отсюда следует, что примененное неравенство Коши превратилось в равенство. Следовательно, имеем
, 
, или 
Ответ: 9.
5)Найдите наименьшее целое решение неравенства
(задание 15)
Решение: Найдя корни уравнения 
, разложим квадратный трехчлен на множители; применив к заданному неравенству другие преобразования, запишем его в виде 
(*)
Применим следствие (1) неравенства Коши: 
Тогда неравенство (*) равносильно системе 
Решая ее стандартным способом, получим 
Ответ: -1
6) Доказать, что 
, где 
— стороны треугольника, а 
— его площадь (задание 16)
Решение: Известно, что 
, где 
— угол между сторонами 
. Так как 
, то 
.
Используя следствие неравенства Коши 
, получаем верхнюю оценку площади треугольника 
. По аналогии получаем 
,
Тогда 
7) В бассейн проведены три трубы. Первая труба наливает 30 м 3 воды в час. Вторая труба наливает в час на 3V м 3 меньше, чем первая (0 3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом? (задание 17)
Решение: Пусть объем бассейна равен A м 3 . Первая и вторая трубы, работая вместе t1 ч, налили
м 3 бассейна,
далее все три трубы, работая вместе t2ч, налили
м 3 бассейна.
В результате бассейн был налит полностью.
Применимследствие неравенства Коши 
. Рассмотрим произведение 
Ясно, что знаменатель полученной дроби имеет наибольшее значение в точке 
имеет наименьшее значение в точке 
. Следовательно, выражение 
также будет иметь аналогичное значение в той же точке . При этом:
Итак, при получим 
. А это значит, что в точке выражение t1 + t2 также примет наименьшее значение. Ответ:
8) При каком действительном р уравнение имеет решение
(задание 18)
Решение. Преобразуем уравнение к виду
и
—неравенство Коши
Используя неравенство Коши, имеем: 2+4 
2=р-7, р=17 Ответ: 17
Этап проведения самостоятельной работы.
Цель: выявить эффективность дополнительного занятия «Неравенство Коши при решении заданий ЕГЭ».
Выявление эффективности проводилось с помощью проверочной работы (Приложение 2 ), посредством содержания которой выявлялись умения:
a) выбрать опорное неравенство Коши (в отличие от стандартных методов);
b) правильно применить опорное неравенство;
c) выполнить преобразования, приводящие к результату.
VI . Этап подведения итога занятия
Цель: обобщить полученные знания и умения на занятии.
Определение уровня усвоения темы по технологии В.П.Беспалько
Обработка результатов, полученных по итогам самостоятельной работы, была проведена в соответствии с технологией, предложенной В.П.Беспалько. По данной технологии нами рассчитывался коэффициент качества усвоения, численное значение которого определяется из соотношения: 
, где 
— коэффициент качества усвоения; 
— число правильно выполненных операций; 
— число всех операций.
Была составлена таблица уровня выполнения заданий проверочной работы (Приложение 3 ).
В таблице ставился «1», если учащийся выполнил умение в том или ином задании и «0», если не выполнил.
Полученные результаты сравнили с уровнями, предложенными В.П.Беспалько: 
— низкий, 
— средний, 
— высокий (Приложение 3).
Анализ результатов по В.П.Беспалько показал эффективность изучения неравенства Коши при решении заданий ЕГЭ.
Одним из достоинств использования неравенства Коши является краткость решения заданий и что иногда оно является единственным способом. Если понимать суть данного метода, то он будет отличным помощником в решении многих задач. А недостатком является то, что далеко не каждый ученик способен понять принцип работы метода. Результатом моей работы стали знания, с помощью которых можно сложные задачи решать очень просто. Обобщив и систематизировав знания о неравенстве Коши, я убедился в необходимости его изучения. Кроме того, эти знания повышают интерес к математике, как к науке. В ходе работы я приобрел навыки решения заданий ЕГЭ, используя неравенство Коши. Думаю, что проделанная мною работа поможет мне успешно подготовиться к экзамену.
— Супрун В. П. Математика для старшеклассников: Задачи повышенной сложности / В.П. Супрун. – М. : Издательство ЛКИ, 2008. – 200с.
— Берколайко С.Т. Использование неравенства Коши при решении задач.- М.: Квант, 1975.- №4.
— Семенов А.Л., ГИА: 3000 задач с ответами по математике. – М.: Издательство «Экзамен», 2014.
— Балаян Э. Н. Практикум по решению задач. Иррациональные уравнения, неравенства и системы/ Э.Н. Балаян. – Ростов н/Д: Феникс,2006. – 120 с.
— Вавилов В. В. Задачи по математике. Уравнения и неравенства/ В.В. Вавилов, И.И. и др. – М.: ФИЗМАТЛИТ, 2007. – 248 с
— Гомонов С. А. /Замечательные неравенства: способы получения и примеры применения. 10-11 кл.: учебное пособие / С.А Гомонов. – М.: Дрофа, 2006. – 254 с.
— Горская Е. С. Решение уравнений и систем, доказательство неравенств, нахождение наименьшего (наибольшего) значения функции / Е.С. Горская // Математика в школе. – 2008. – №8. – С. 48–49.
— Сивашинский И. Х. Неравенства в задачах/ И.Х. Сивашинский. – М.: Наука, 1967. – 213 с.
— Седракян Н.М. Авоян А.М. Неравенства. Методы доказательства. – М.: Физматлит, 2002.
— Сивашинский И.Х. Неравенства в задачах. – М.: Наука, 1967.
— Сорокин Г. А. Классические неравенства в задачах/ Г.А. Сорокин // Математика в школе. – 2005. – №3. – С. 35–41.
— Фирстова Н. И. Решение некоторых видов уравнений при помощи неравенств / Н.И. Фирстова // Математика в школе. – 2002. – №1. – С. 29–33.
— Чистяков И. Неравенства Коши о средних арифметическом и геометриче- 86 ском / И. Чистяков // Математика в школе. – 2000. – №7. – С. 18–24.
— Математика. 9 класс. Подготовка к ЕГЭ – 2019. Под редакцией Ф,Ф, Лысенко, С.Ю. Кулабухова. Учебно – методическое пособие- М.: «Легион – М», 2018 г.
— ЕГЭ 2019. Математика. Профильный уровень. Под редакцией И.В.Ященко, И.Р.Высоцкий, М.А.Волчкевич- М.: «Экзамен», 2019.- 264с.
Анализ содержания на изучение неравенства Коши в школьных учебников
Автор и название учебника
Изучение неравенства Коши
Алгебра 8 кл., учебник для классов с углубленным изучением математики
Рассматривается определение средних арифметического и геометрического; доказывается неравенство среднее арифметическое 2-х положительных чисел не меньше их среднего геометрического; примеры доказательства.
Алгебра 8 кл., учебник для общеобразовательных учреждений
Рассматривается пример о соотношении среднего арифметического, среднего геометрического и среднего гармонического положительных чисел
Алгебра 9 кл., учебник для классов с углубленным изучением математики
Алгебра 9 кл., учебник для общеобразовательных учреждений
Алгебра 8 кл., учебник для общеобразовательных учреждений
Алгебра 9 кл., учебник для общеобразовательных учреждений
В дополнении к главе «Неравенства» дается определение средних арифметического и геометрического; доказывается неравенство Коши для 2-х чисел: рассмотрены примеры доказательства неравенств с помощью неравенства Коши
Задания повышенной трудности, предназначенные для изучения в классах с углубленным изучением математики
Алгебра и начала анализа 10 кл., учебник для общеобразовательных учреждений
В параграфе «Доказательство числовых неравенств» доказывается неравенство среднее арифметическое 2-х положительных чисел не меньше их среднего геометрического; приводятся примеры доказательства неравенств с помощью доказанного неравенства.
Представлен параграф под знаком *, то есть как углубленное изучение, не обязательное для общеобразовательных классов.
Никольский С.М. Алгебра и начала анализа 11 кл., учебник для общеобразовательных учреждений
В параграфе «Нестандартные методы решения уравнений и неравенств» описывается применение неравенства Коши при n=2 для решения неравенств и уравнений. Не говорится, что используется неравенства Коши при n=2
Представлен параграф под знаком *, то есть как углубленное изучение, не обязательное для общеобразовательных классов.
Алгебра 8 кл., учебник для классов с углубленным изучением математики
Алгебра 9 кл., учебник для классов с углубленным изучением математики
Алгебра и начала анализа 10 кл., учебник для классов с углубленным изучением математики
Алгебра и начала анализа 11кл., учебник для классов с углубленным изучением математики
В параграфе «Доказательство неравенств с несколькими переменными» дается определение неравенства Коши, его доказательство и примеры доказательства неравенств с помощью неравенства Коши.
Алгебра и начала анализа 10-11 кл., учебник для общеобразовательных учреждений
Алгебра и начала анализа 10-11 кл., учебник для общеобразовательных учреждений
Алгебра и начала анализа 10 кл., учебник для общеобразовательных учреждений
В параграфе «Доказательство неравенств» рассматривается пункт «Классические неравенства». Даются определения средних арифметического и геометрического, неравенства Коши; приводится доказательство этого неравенства; рассматриваются примеры
Представлен параграф под знаком *, то есть как углубленное изучение, не обязательное для общеобразовательных классов
Вариант заданий проверочной работы на дополнительное занятие «Неравенство Коши при решении заданий ЕГЭ»
Найти наименьшее значение функции
Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 
млн рублей в год. Если продукцию завода продать по цене ртыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит 
). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
4. В бассейн проведены три трубы. Первая труба наливает 20 м 3 воды в час. Вторая труба наливает в час на 2V м 3 меньше, чем первая (0 3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 20% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 80% бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?
Уровень выполнения заданий проверочной работы
Видео:Неравенство Коши о среднихСкачать
«Применение неравенства Коши к доказательству неравенств и решению задач как эффективный способ доказательства гипотез»
Использование неравенства Коши и следствий из него является одной из теоретических основ при решении задач на доказательство и решение неравенств. В настоящей работе описывается применение неравенства Коши к решению заданий из курса алгебры 8-9-х классов. Так как отдельной темой неравенство Коши в школьном курсе не изучается, то его использование делает решение отдельных неравенств и уравнений не только простым, но иногда единственно возможным.
Цель работы: познакомиться с творческой биографией Огюстена Луи Коши, рассмотреть доказательство неравенства, носящего его имя. На основе решенных задач, используя неравенство Коши, сделать вывод об эффективности применения этого метода к решению различных задач.
Гипотеза: неравенство Коши является эффективным способом доказательства гипотез и может быть использовано при решении многих задач математики и физики.
Задачи: изучить научно-популярную и специальную литературу по теме исследования; рассмотреть основные положения неравенства Коши и следствия из него; выявить виды математических и физических задач, где можно было бы применить неравенство Коши; сделать вывод.
В работе подробно рассматриваются определения и доказательство среднего арифметического, среднего геометрического, среднего гармонического и других средних величин.
Предложены примеры задач, где можно применить доказанное неравенство. Это такие задачи, как: исследование функций, нахождение их наибольших и наименьших значений; решение уравнений и систем уравнений; решение геометрических, текстовых, прикладных, физических и олимпиадных задач.
Доказав неравенство Коши и изучив следствия из него, автор сделал вывод:
— среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического;
— длина медианы, проведенной к гипотенузе прямоугольного треугольника, не меньше длины высоты, проведенной к гипотенузе;
— неравенство между средним арифметическим и средним геометрическим может применяться при решении задач на нахождение экстремумов, то есть наибольших и наименьших значений функций;
— одним из достоинств метода является легкость решения задач с его применением.
Настоящая работа может быть полезна выпускникам 9-х и 11-х классов при подготовке к государственной итоговой аттестации.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Скачать:
| Вложение | Размер |
|---|---|
| Неравенство Коши | 154.87 КБ |
Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать
Предварительный просмотр:
Государственное бюджетное общеобразовательное учреждение
лицей №395 Красносельского района Санкт-Петербурга
(ГБОУ лицей № 395 Санкт- Петербурга)
«Применение неравенства Коши к доказательству
неравенств и решению задач как эффективный
способ доказательства гипотез»
Сахаров Артур, 9в класс
Первушкина Ирина Михайловна,
педагог дополнительного образования
ГБОУ лицея № 395
2017 – 2018 учебный год
2.1. Биография Огюстена Луи Коши …………………………………. 5
2.2. Неравенство Коши и его доказательство ..………………………………… 5
2.3. Применение неравенства Коши к доказательству гипотез и
решению задач математики и физики…………………………………………..7
На уроках алгебры в 8 классе мы изучали доказательство неравенств, одним из неравенств мы рассмотрели неравенство, носящее название «Неравенство Коши», а также понятие о среднем арифметическом, а на уроке геометрии о среднем геометрическом. Я увидел связь между названными понятиями. И это оказалось действительно так. Меня заинтересовал этот факт, и я решил подробно изучить неравенство Коши, рассмотреть применения его к решению других задач. Подробное знакомство с различными методами доказательства гипотез может быть полезно мне не только для расширения кругозора, но также и потому, что на его принципе основано решение многих задач (включая олимпиадные). Мною был изучен принцип доказательства неравенств, а также его широкое применение в решении задач на доказательство и решение неравенств, при решении уравнений и систем уравнений, геометрических и физических задач.
Как оказалось, неравенство Коши актуально и в математике и в физике, в геометрии, даже в астрономии! В школьном курсе 8-9 класса изучают лишь малую часть интересной теоремы, которая заключает в себе гораздо больше, чем две строчки в учебнике геометрии. И я захотел сделать своеобразную исследовательскую работу по этой теме.
При решении задач, предлагаемых на экзаменах ОГЭ и олимпиадах по математике, могут быть использованы любые известные выпускникам математические методы. При этом разрешается пользоваться и такими, которые не изучаются или изучаются в ознакомительных целях в общеобразовательной школе. Все это свидетельствует о необходимости самостоятельного изучения выпускниками математических методов, в основе которых лежат понятия и положения, не входящие в программу по математике общеобразовательной школы. К таким понятиям, например, относится неравенство Коши и многие другие.
Данная работа рассчитана на учащихся, которые имеют довольно-таки высокий уровень знаний в области математики, причем как в пределах, так и вне школьной программы, но все равно хотят его повысить.
В работе описывается применение неравенства Коши к решению заданий из курса алгебры 8-9-х классов. Так как отдельной темой неравенство Коши в школьном курсе не изучается, то его использование делает решение отдельных неравенств не только простым, но и красивым.
Прочитав специальную литературу, я понял, что с помощью неравенства Коши можно решать разные виды задач. Передо мной появилась задача, требующая исследования, которой я решил посвятить свою работу.
Цель работы : познакомиться с творческой биографией Огюстена Луи Коши, рассмотреть доказательство неравенства, носящего его имя. На основе решенных задач, используя неравенство Коши, сделать вывод об эффективности применения этого метода к решению различных задач.
Гипотеза: неравенство Коши является эффективным способом доказательства гипотез и может быть использовано при решении многих задач математики и физики.
— изучить научно-популярную и специальную литературу по теме исследования;
— рассмотреть основные положения неравенства Коши и следствия из него;
— доказать неравенство Коши самостоятельно;
— выявить виды математических и физических задач, где можно было бы применить неравенство Коши;
Методы исследования: анализ математической литературы и ресурсов Интернета по данной теме; репродуктивное воспроизведение изученного материала; познавательно — поисковая деятельность; анализ и сравнение данных в поиске материала; сравнение и обобщение математических фактов; анализ полученных результатов.
Краткий обзор использованной литературы. Прочитав подборки статей в журналах «Квант» , я рассмотрел некоторые виды задач, где применяется неравенство Коши. В книге « Избранные вопросы математики. 9 класс. Факультативный курс» авторов Боковнев О. А., Фирсов В. В., Шварцбурд С. И. я узнал много интересных фактов о жизни и научной деятельности Огюстена Коши, изложенных и систематизированных в понятной и доступной форме. Информацию о доказательстве неравенства я узнал из учебника «Алгебра и математический анализ 10 класс». На страницах Википедии «Коши Огюстен» я узнал биографию ученого и некоторые задачи, решенные им. Среднее геометрическое и другие средние хорошо рассмотрены в книге « Геометрия. Дополнительные главы к учебнику. 8 кл» авторов Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Шестаков С.А., Юдина И.И. Различные виды задач, которые можно решить рассматриваемым методом, я взял из учебников « Алгебра и начала математического анализа. 10 класс» Мордковича А.Г. и « Геометрия, 7 – 9» Атанасян Л.С., Бутузов В.Ф. и др., а также из сборников для подготовки к ГИА, олимпиадных заданий. Некоторые задачи и теоретические факты я рассмотрел на страницах сайта https://MathUs.ru и из книги «Сборник задач по алгебре для 8 – 9 кл.» авторов Галицкий М. Л., А.М. Гольдман, Л.И. Звавич.
- Основная часть
- Биография Огюстена Луи Коши
А начать свою работу хочется с биографии учёного, в честь которого назвали неравенство. Огюстен Луи Коши родился в 1789 году в семье адвоката. Из истории мы помним, что в этом же году стартовала череда событий «Великая Французская Революция». И что Коши стал великим учёным в такой трудной обстановке действительно о чём-то говорит. Соседями семьи Коши были двое учёных. Первый астроном и физик, которого звали Пьер Симон Лаплас, а второй был химиком по имени Клод Луи Бертолле. Эти двое учёных вместе с Жозефом Лагранжом оказали серьезное влияние на Огюстена, в частности, на его любовь к математике. И однажды Лагранж сказал: «Этот мальчик как геометр заменит всех нас». Потом Коши отдают в престижную Центральную школу Пантеона. После её окончания он поступает в Политехническую школу, которую оканчивает через два года. Во время учебы в Политехнической школе он с большим успехом изучал математику. Дальше он в числе первых поступает в школу мостов и дорог.
В 1811-1812 гг. Коши представил несколько работ в Парижскую академию наук. А в 1813г. переехал в Париж, где занялся научной и преподавательской работой в Политехнической школе. А в 1816 году становится членом Парижской академии наук. [10]
Огюстен Луи Коши написал более 800 работ, полное собрание его сочинений содержит 27 томов. Его работы относятся к различным областям алгебры, геометрии и математической физики. Также стоит сказать, что он был отличным механиком и инженером.
- Неравенство Коши и его доказательство
Для начала рассмотрим определения среднего арифметического, среднего геометрического, среднего гармонического и других средних величин.
- Среднее арифметическое — это сумма всех чисел, делённая на их количество.
Для двух чисел: (a + b) / 2 (где a, b два различных неотрицательных числа); для трех чисел:
(a + b + c)/3; д ля четырёх чисел: (a+b+c+d)/4; для n чисел: (a 1 +a 2 +a 3 +…a n )/n.
- Средним геометрическим для n положительных чисел а 1 , а 2, . а n называется
такое положительное число а, что а n = а 1 а 2 … а n , обозначается так: .
- Средним гармоническим для чисел a и b называется число с, определяемое равенством , где с = .
- Средним квадратичным для чисел а и b называется число с = . [3]
Задача 1 . Пусть a и b неотрицательные числа. Доказать, что (*)
Доказательство . Составим разность левой и правой частей неравенства:
В итоге получили неотрицательное число, значит
Равенство левой и правой частей неравенства достигается, только тогда, когда a = b, если a≠ b, то
Таким образом, с реднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Это неравенство называют неравенством Коши в честь французского математика Огюстена Луи Коши. [7]
Докажем неравенство (*) для нескольких слагаемых.
- Для четырех чисел неравенство Коши имеет вид: . (**)
Неравенство (**) станет равенством при a = b, c = d, , то есть при a = b = c = d.
- Для трех чисел неравенство Коши имеет вид: .
Доказательство : , откуда a + b + c ≥ .
Равенство в нем достигается при a = b = c.
Следствия из неравенства Коши:
- Для любого положительного числа а справедливо неравенство а + (***)
Причем равенство получится, если а = 1. Т.е. сумма двух положительных взаимно обратных чисел не меньше двойки, причем равенство достигается, когда оба они равны единице.
- Пусть а 1 , а 2 , …, а n неотрицательные числа, тогда верно неравенство
- Неравенство Коши можно записать в следующем виде:
, a 2 + b 2 ≥ 2ab, a 2 + b 2 + c 2 ≥ 3 . [9]
4. Запишем неравенство Коши для пар чисел
Т.е. =2 . Сложив эти неравенства, получим: По теореме о среднем арифметическом и среднем геометрическом получим неравенство С учетом последнего неравенства неравенство может быть записано следующим образом
Неравенство Коши имеет любопытное геометрическое истолкование. Пусть дан прямоугольный треугольник и пусть высота h, проведенная из вершины прямого угла, делит гипотенузу на отрезки a и b. В геометрии доказано, что h = . А что такое ? Это длина половины гипотенузы. Но из геометрии известно, что медиана прямоугольного треугольника, проведенная из вершины прямого угла равна половине гипотенузы. Таким образом, неравенство Коши означает, что длина медианы, проведенной к гипотенузе, не меньше длины высоты, проведенной к гипотенузе. [7]
Средним геометрическим для n положительных чисел а 1 , а 2, . а n называется
такое положительное число а, что а n = а 1 а 2 … а n , обозначается так: .
2.3. Применение неравенства Коши к доказательству гипотез и решению
задач математики и физики
Доказанное неравенство Коши можно применять в решении многих задач, таких как:
— при доказательствах неравенств;
— при решении задач на исследование функций, нахождении их наибольших и наименьших значений;
— при решении уравнений и систем уравнений;
— при решении геометрических задач;
— в решении задач прикладного характера и текстовых задач;
— в решении задач физического содержания;
— в решении олимпиадных задач.
Рассмотрим примеры применения неравенства Коши.
Пример 1. Докажите неравенство .
Решение. Перенесем все слагаемые в одну часть и приведем подобные слагаемые
. Применим к левой части формулу квадрата разности
Каждое из слагаемых полученного выражения неотрицательно, это доказывает справедливость требуемого неравенства. Равенство достигается лишь в том случае, когда . Неравенство доказано.
Пример 2. Докажите, что при a > 0, b > 0, c > 0, d > 0 верно неравенство
(a + b)(b + c)(a + c) ≥ 8abc.
Доказательство : воспользуемся формулами о среднем арифметическом и среднем геометрическом, которые мы рассмотрели ранее, для чисел a, b, c, d получим: При данных условиях правая и левая части неравенств положительны, а значит, их можно почленно перемножить: 
Получим неравенство (a + b)(b + c)(a + c) ≥ 8abc. Что и требовалось доказать.
Пример 3. Докажите неравенство .
Решение. Данное неравенство можно доказать с помощью неравенства Коши. Разложим второе слагаемое в заданном неравенстве на сумму двух слагаемых и сгруппируем слагаемые так как нам удобно:
Применим к выражению в скобке неравенство Коши
Полученному применим еще раз неравенство Коши
Таким образом, третий раз применив неравенство Коши, доказали неравенство. В цепочке соотношений трижды применялось неравенство Коши для двух положительных чисел. [3]
Пример 4. Решить уравнение [3]
Решение . Данное уравнение задано для х ≥ 0 и легко видеть, что в области допустимых значений левая часть уравнения всегда положительна. Преобразуем левую часть уравнения следующим образом:
Применяя неравенство Коши, будем иметь
в котором равенство достигается лишь тогда, когда 
Решая это уравнение, находим корни х 1 = 1, х 2 = 4. Так как оба найденных значения положительны, то это и есть искомые корни заданного уравнения. Ответ: х 1 = 1, х 2 = 4.
Пример 5. Решить систему уравнений х ≥ 0, у ≥ 0 .
Решение. Так как х ≥ 0, у ≥ 0, то к левой части первого уравнения системы можно применить неравенство Коши, где n = 3.
Отсюда, из первого уравнения системы следует, что примененное неравенство превратилось в равенство. А это означает, что выполняется условие x 3 = 27 y 3 или x = 3y.
Подставим x = 3y во второе уравнение системы и получим 9y 2 – 3y 2 + y 2 = 28 или y 2 = 4.
Так как у ≥ 0 и x = 3y, то y 1 = 2 и x 1 = 6. Ответ: y 1 = 2 и x 1 = 6.
Эту систему уравнений я пытался решить другим способом, но мне он показался очень трудоемким, оптимальный способ – это применение неравенства Коши.
Пример 6. При каком значении высоты прямоугольная трапеция с острым углом 30 0 и периметром 6 см имеет наибольшую площадь? [6]
Решение : Пусть х см – высота трапеции, следовательно боковая сторона тоже равна х см, сторона ВС равна y см.
Тогда периметр равен Р = 3х + 2y + х, откуда 2y = 6 – 3х — х.
Найдем площадь участка S = x = x = .
Найдем наибольшее значение площади, решив уравнение 2 – х = х.
Равенство достигается при х = 1.
Ответ: При длине высоты трапеции, равной 1 см, её площадь принимает наибольшее значение.
Задачи по физике
Пример 7 . Автомобиль едет из пункта А в пункт В со скоростью 60 км/ч. В пункте В он едет с ускорением а до полной остановки. Затем он начинает двигаться равноускоренно в противоположном направлении. Какого должно быть значение а , чтобы после 3 часов после возобновления движения автомобиль находился ближе к пункту В?
Решение . Равенство достигается, если
Откуда найдем ускорение а = v 0 /t = 60/3 = 20 км/ч 2 . Ответ: а = 20 км/ч 2 .
Пример 8 . Конькобежец проходит дистанцию l=500м с постоянной скоростью v, а затем тормозит с ускорением a = 0,05м/с 2. При какой скорости время движения конькобежца до остановки наименьшее? [7]
Решение. Время движения, очевидно. состоит из двух слагаемых: времени движения с постоянной скоростью и времени равнозамдлительного движения до полной остановки:
t = . А наименьшее время движения t min= . достигается при равенстве слагаемых т.е при v =5м/с.
А теперь рассмотрим задачи, содержащиеся в сборниках для подготовки к ГИА [3]
Среднее геометрическое трех чисел a, b, c вычисляется по формуле g = . Вычислите среднее геометрическое чисел 3, 9, 27.
Среднее квадратичное трех чисел a, b, c вычисляется по формуле q = . Вычислите среднее квадратичное чисел 2, 11 и 5 .
Неравенство между средним арифметическим и средним геометрическим может применяться при решении задач на нахождение экстремумов, то есть наибольших и наименьших значений функций.
Пример 11. Число 10 разбить на два слагаемых так, чтобы их произведение было наибольшим.
Решение. Пусть 10 = x + y. Предположим, что x >0 и y > 0. Применяя неравенство (*), имеем: . Т.е. ху ≤ 25. Значит, наибольшее значение произведения ху, равное 25, достигается при х = у = 5. Ответ. 10 = 5 + 5.
Пример 12. Найти наименьшее значение функции при х > 0.
Решение : запишем функцию в виде
Значит, наименьшее значение функции при х > 0 равно 6 и достигается при , то есть при х = 4. Ответ: наименьшее значение функции равно 6.
Пример 13. Найдите наименьшее значение функции [6]
Решение. Разобьем свободный член на сумму 4 и 1 и представим в виде
Применим неравенство Коши для двух взаимообратных чисел, тогда:
Прибавим к обеим частям неравенства свободный член 4 и получаем, что – наименьшее значение функции, которое достигается только при . Следовательно,
Пример 14 . Решите уравнение:
Решение. Решим это уравнений, используя следствие 1 из неравенства Коши (***).
Левую часть уравнения можно записать в виде:
Правую часть уравнения можно записать в виде:
Равенство может иметь место лишь в том случае, когда левая и правая части уравнения равны. Значит так и будет при х = 1. Проверкой убеждаемся, что х = 1 решение уравнения. Ответ: х = 1.
Пример 15 . Самолет пролетел путь от А до Б по ветру и путь от В до А против ветра, причем скорость ветра не менялась. В другой раз самолет совершил рейс по тому же маршруту в безветренную погоду. В обоих случаях моторы самолета развивали одинаковую мощность. В каком случае на весь полет ушло меньше времени? [5]
Решение. Пусть скорость самолета х км/ч, а скорость ветра у км/ч. В первый раз самолет затратил на путь , а во второй раз , где S – расстояние АВ.
Следовательно, и значит, во второй раз самолет пролетит быстрее.
Ответ: в безветренную погоду на весь полет ушло меньше времени.
Пример 16. Из квадратного листа жести со стороной a изготавливается коробка в виде прямоугольного параллелепипеда. Для этого в углах листа вырезаются четыре квадратных куска, и получившаяся фигура складывается по линиям разреза. Найти максимально возможный объём такой коробки. [3]
Решение: сделаем рисунок
Обозначим сторону квадрата х. Тогда в основании коробки получается квадрат со стороной a − 2x, а высота коробки равна x. Объём коробки: V = x(a − 2x) 2 или запишем по-другому
Используя неравенство Коши, имеем:
Откуда . Максимальное значение объема равно достигается при x . Ответ: максимально возможный объём коробки равен
Пример 17 . Средний возраст одиннадцати футболистов 28 лет. Во время игры один из игроков был удалён и средний возраст оставшихся стал равен 27лет. Сколько лет удалённому игроку? [6]
Решение: с редний возраст одиннадцати футболистов найдем как среднее арифметическое чисел по формуле = 28 , а средний возраст десяти футболистов найдем как среднее арифметическое чисел по формуле = 27.
Составим и решим систему уравнений:
, откуда найдем а 11 = 308 – 270 = 38.
Ответ: Удаленному игроку 38 лет.
Использование неравенства Коши и следствий из него является одной из теоретических основ при решении задач на доказательство и решение неравенств, при решении геометрических и физических задач, решении уравнений и систем уравнений и т. д.
Знакомясь с неравенством Коши, я изучал специальную литературу, консультировался с учителем математики, анализировал данные и решения задач, пользовался ресурсами Интернета, выполнял необходимые вычисления.
В ходе работы я узнал, чтобы решать задачи с помощью неравенства Коши нужно знать и активно применять на практике различные средние: арифметическое, геометрическое и другие. А также необходимо «видеть», где использовать эти неравенства.
Одним из достоинств метода является легкость решения задач с его применением. И действительно можно сказать, что неравенство Коши гораздо более эффективно, нежели обычный способ решения, а иногда он является единственным. Если понимать суть данного метода, то он будет отличным помощником в решении многих задач. А недостатком является то, что метод сложен в понимании, и далеко не каждый ученик способен понять принцип работы метода. Результатом моей работы стали знания, с помощью которых можно сложнейшие задачи решать очень просто. Ведь для этого и нужны подобные теоремы, чтобы облегчить и упросить нам решения. Обобщив и систематизировав знания доказательства неравенств с помощью неравенства Коши, я убедился в необходимости его изучения. Кроме того, эти знания повышают интерес к математике, как к науке. В ходе работы я приобрел навыки решения задач, используя неравенство Коши. Считаю, что эти навыки помогут мне в будущем.
Во время изучения специальной литературы я узнал, что неравенство Коши имеет большое применение, оно всего лишь часть теоремы доказанной Коши, а называется она теорема о среднем. И в будущем я планирую изучить подробно и эту теорему.
🔍 Видео
#167. НЕРАВЕНСТВО КОШИ О СРЕДНИХ!Скачать
✅ Неравенство Коши #shortsСкачать
НЕРАВЕНСТВА | МУНИЦИПАЛЬНЫЙ ЭТАП ВСОШСкачать
Пример 65. Решить задачу Коши (диффуры)Скачать
Бельчонок-2023. Жесткое неравенствоСкачать
Неравенство Коши | Профильная МатематикаСкачать
Как решать неравенства? Часть 1| МатематикаСкачать
Доказательство неравенств Неравенство КошиСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Решение неравенства методом интерваловСкачать
Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать
Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать
АЛГЕБРА на региональном этапе ВсОШ // неравенство Коши, анализ функцийСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
