Применение метода максимального правдоподобия в оценке параметров уравнения множественной регрессии (2 видео)

Оценка параметров регрессии по методу максимального правдоподобия

Для того чтобы использовать МНК при оценке параметров регрессии, необходимо выполнение ряда предпосылок (условий Гаусса — Маркова). Такие предпосылки ограничивают применимость метода. На практике они часто не выполняются. В некоторых случаях оценки МНК несостоятельны, и желательно получение альтернативных им состоятельных оценок. Кроме того, МНК наиболее удобен для линейных моделей или моделей, сводящихся к линейным (т.е. линеаризуемых).

Альтернативой МНК является так называемый метод максимального правдоподобия (ММП), который также позволяет оценивать параметры линейного регрессионного уравнения по данным наблюдений. Более того, ММП позволяет оценивать параметры не только линейных регрессий, но и нелинейных регрессионных уравнений.

Недостатком ММП по сравнению с МНК следует признать сложность вычислительной процедуры получения оценок, которая является итерационной вследствие нелинейности уравнений, связывающих данные наблюдений с оценками параметров.

Покажем, что для линейной парной регрессии в случае нормального закона распределения случайной величины е, оценки параметров поМНКиММП совпадают.

Предположим, что мы ищем параметры парной линейной регрессии (1.3):

Согласно условиям Гаусса — Маркова ошибки регрессии е, независимы и распределены по нормальному закону:

Перепишем выражение (1.58) с учетом (1.3′):

Имея набор наблюдений (х, ,у,), / = 1, п, мы можем попытаться ответить на вопрос: при каких значениях параметров а, Ь, о 2 модели (1.3′), с учетом выражения (1.58), вероятность получить этот набор наблюдений наибольшая?

Для ответа на этот вопрос составим так называемую функцию правдоподобия. При этом будем рассматривать у, как независимые нормальные случайные величины с математическим ожиданием Г, = ), являющимся функцией от х„ согласно формуле (1.3′),

и постоянной дисперсией а 2 . Тогда плотность вероятности наблюдения у, запишется так:

Функция правдоподобия показывает совместную плотность вероятности одновременного появления всех п наблюдений у, и равна произведению выражений (1.60):

Согласно принципу максимального правдоподобия, наиболее правдоподобными величинами параметров а, Ь, о 2 будут такие, которые обеспечивают максимальное значение функции (1.61).

Для нахождения таких оценок следует продифференцировать функцию (1.61) по каждому из параметров, а затем приравнять производные нулю (условия первого порядка).

Решение полученной системы обеспечивает выполнение необходимого условия максимума. Для проверки выполнения достаточных условий максимума следует взять вторые производные, подставить в них значения параметров, полученные из условий первого порядка, определить выполнимость условий второго порядка. Для функции (1.61) такая непосредственная процедура является очень сложной и громоздкой (дифференцирование произведения большого числа функций с повторным дифференцированием еще большего выражения и т.д.). Поэтому она была упрощена заменой функции (1.61) ее логарифмом In L. Тогда вместо произведения выражений для плотностей вероятности получаем их сумму:

Так как функция логарифма является монотонно возрастающей функцией L, то функции L и In L в формулах (1.61) и (1.62) одновременно достигают своего максимума.

Запишем необходимые условия для логарифмической функции правдоподобия:

Решением системы уравнений (1.63) — (1.65) являются оценки максимального правдоподобия:

Отсюда видно, что оценки (1.66) для параметров а и b совпадают с оценками МНК (1.7) и (1.8). Это является следствием того, что уравнения (1.63) и (1.64) совпадают с соответствующими уравнениями МНК. Однако оценка ст^_(МП не совпадает с остаточной дисперсией (1.17), которая является несмещенной оценкой остаточной дисперсии. Таким образом, оценка а^_мп является смещенной, но тем не менее состоятельной оценкой остаточной дисперсии.

Функция правдоподобия находит применение не только в оценивании параметров нелинейных регрессий. Она используется также в оценивании качества отдельных видов регрессий, где обычные меры качества, такие как индекс детерминации, не имеют смысла. В качестве примера можно привести упоминаемые выше логистические регрессии, где зависимая переменная представляет собой вероятность какого-либо события и в каждом наблюдении принимает только два значения 0 или 1. В этих случаях некоторые регрессионные пакеты рассчитывают коэффициент псевдо-Л 2 , сравнивающий логарифм функции правдоподобия In ? с тем логарифмом функции правдоподобия In L₀, который был бы получен при включении в уравнение регрессии только свободного члена.

Функция правдоподобия показывает совместную вероятность и поэтому может принимать значения в интервале от 0 до 1. Следовательно, логарифм правдоподобия должен быть отрицательным. Коэффициент псевдо-i? 2 включает отношение, в котором In L по абсолютной величине меньше, чем In L₀:

Минимум этой величины равен нулю, а ее максимум — меньше единицы, но в отличие от коэффициента R 2 она не имеет естественной интерпретации. Тем не менее вариации значения функции правдоподобия, как и вариации суммы квадратов отклонений в стандартной регрессии, могут служить основой для выполнения статистических тестов. Например, объясняющая способность модели может быть протестирована с помощью статистики «отношение правдоподобия», или ?7?-статистики:

которая имеет распределение у 2 с т степенями свободы, где т — число параметров при объясняющих переменных. Здесь нулевая гипотеза предполагает, что все коэффициенты при объясняющих переменных одновременно равны нулю.

Содержание

Применение метода максимального правдоподобия для оценки параметров множественной линейной регрессионной модели
Метод максимального правдоподобия с примерами
Методы нахождения оценок
Готовые работы на аналогичную тему
Сущность метода максимального правдоподобия
Пример использования метода максимального правдоподобия
📺 Видео

Видео:13-02 Линейная регрессия и метод максимального правдоподобияСкачать

Применение метода максимального правдоподобия для оценки параметров множественной линейной регрессионной модели

Метод максимального правдоподобия с успехом может быть применен и для нахождения параметров линейной регрессионной модели. Продемонстрируем это на примере парной регрессии.

Пусть Y_t = р₍₎ + pjX_y + . г = 1. п, причем ошибки взаимно независимы и имеют нормальное распределение: 8,

Поскольку 8-, i=l. Пу независимы и распределены нормально, то функция правдоподобия имеет вид

а логарифмическая функция правдоподобия —

Необходимым условием экстремума является равенство нулю частных производных по Р₍₎, pj и а 2 :

Легко заметить, что первые два уравнения точно такие же, как и в системе нормальных уравнений для оценок МНК (см. формулу (3.6)), поэтому мы сразу можем выписать решения:

Из последнего уравнения несложно найти оценку для дисперсии оши- r ее

—(напомним, что RSS определено формулой (3.3)).

Можно показать, что и в данном случае выполнены достаточные условия максимума (см. задание 6.3), поэтому найденные оценки являются ММП-оценками.

Замечание 6.1. Если оценки максимального правдоподобия коэффициентов р₍₎ и р, совпадают с МНК-оценками и, следовательно, являются несмещенными (см. параграф 4.1), то ММП-оценка дисперсии ошибок является смещенной (как отмечалось в подпараграфе 4.2.1, несмещенная оценка

дисперсии ошибок есть а 2 = ——z).

ММП-оценки коэффициентов множественной регрессии можно получить аналогично, но, чтобы избежать громоздких формул, лучше использовать матричный аппарат, как это сделано в параграфе 5.1.

N(0. а%), 0„ — /г-мериый нулевой вектор, 1_Я — и-мерная единичная матрица (напомним, что определение случайного вектора, имеющего совместное нормальное распределение, было дано в параграфе 2.2), функция правдоподобия имеет вид

а логарифмическая функция правдоподобия —

Учитывая правила дифференцирования по вектору (см. параграф 5.1), получаем

Можно показать [1] , что достаточные условия экстремума тоже выполнены, следовательно, полученные оценки являются ММП-оценками.

Как и для случая парной регрессии, МНК- и ММП-оценки коэффициентов множественной регрессии совпадают, а оценка дисперсии ошибок

ст. =-является смещенной (несмещенная оценка а- =—, см. па-

раграф 5.3). Однако на больших выборках это смещение невелико, посколь- 1 1

Видео:12-02 Смысл метода максимального правдоподобияСкачать

Метод максимального правдоподобия с примерами

Вы будете перенаправлены на Автор24

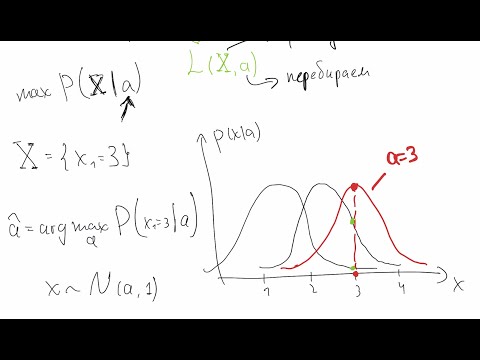
Метод максимального правдоподобия – это рациональный способ построения оценки какого-либо неизвестного параметра, суть которого состоит в том, что за «наиболее правдоподобное» значение параметра принимается значение $Ө$, сводящее к максимуму вероятность получения при $n$ опытах следующую выборку $X = (x_1, …, x_n)$.

Видео:Суть метода максимального правдоподобияСкачать

Методы нахождения оценок

В общем смысле точечная оценка неизвестного параметра $Ө$ – это любая статистика. В практической же деятельности чаще всего рассматриваются самые «качественные» оценки, при которых вероятность принятия ими значения максимально близкого к неизвестному значению $Ө$ при реализации случайной выборки будет наибольшей. Данные оценки делят на несмещенные, состоятельные и эффективные. При этом возникает вопрос о методах получения качественной оценки для произвольного параметра $Ө$ исследуемой случайной величины $X$. Наиболее распространены следующие методы нахождения оценок:

Метод подстановки;
Метод моментов;
Метод наибольшего правдоподобия.

Метод подстановки – это наиболее простой метод отыскания точечных оценок. Он заключается в том, что оценкой неизвестного параметра $Ө$ является соответствующая выбранная числовая характеристика:

Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ

К примеру, по методу постановки оценка математического ожидания – это выборочное среднее, а оценка дисперсии – это выборочная дисперсия.

Все полученные по методу подстановки оценки являются состоятельными, но не гарантирована их эффективность и несмещенность. Пример смещенной оценки – выборочная дисперсия.

Рассмотрим далее метод моментов. Предположим, что $x_1, …, x_n$ – это выборка наблюдений некоторой случайной величины$X$, которая имеет распределение $Fx (x, Ө)$ содержащее вектор неизвестных параметров $Ө =( Ө_1, …, Ө_k)$. Допустим, что для данного распределения можно рассчитать начальные моменты

Готовые работы на аналогичную тему

Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

некоторых порядков $r$.

Такие моменты называются функциями соответствующих неизвестных параметров $Ө_1, …, Ө_k$. Однако, для выборки можно рассчитать выборочные начальные моменты

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ

Метод моментов заключается в том, что необходимо найти такой вектор параметров $Ө$, при котором будут равны теоретические и выборочные моменты, т.е. в решении системы уравнений:

Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ

Число уравнений в данной системе будет равняться количеству неизвестных параметров $k$. Чтобы получить оценки с помощью метода моментов, может быть выбран любой момент произвольного порядка, но, как правило, в практике используются только моменты низших порядков.

Как и при методе подстановок, все оценки, найденные по методу моментов, характеризуются как состоятельные, но не гарантируется их эффективность и несмещенность.

Точечные оценки, найденные при помощи метода моментов, носят название ММ-оценки.

Метод наибольшего правдоподобия рассмотрим в следующем пункте.

Видео:Лекция 17. Метод моментов. Метод максимального правдоподобия.Скачать

Сущность метода максимального правдоподобия

Под методом максимального правдоподобия в математической статистике понимается метод оценки неизвестного параметра посредством максимизации функции правдоподобия. Основой данного метода является предположение о том, что все данные о статистической выборке содержатся в функции правдоподобия. Описываемый метод был проанализирован Р. Фишером в начале 20-го века, который в дальнейшем его рекомендовал и популяризировал.

Оценка наибольшего правдоподобия – это достаточно популярный статистический метод, используемый с целью построения статистической модели на основе информации и обеспечения оценки всех параметров модели.

Метод наибольшего правдоподобия соответствует многим популярным методам статистической оценки. К примеру, вы рассматриваете такой антропометрический параметр, как рост жителей данной страны. Допустим, что вы располагаете данными о росте определенного количества людей, но не всего населения. Помимо этого, допускается, что рост – это нормально распределенная величина со средним значением и неизвестной дисперсией. Дисперсия роста и среднее значение в выборке будут являться максимально правдоподобными к дисперсии и среднему значению всего населения.

Используя фиксированный набор данных и базовой модели вероятностей в расчетах с помощью метода правдоподобия, будут получены такие значения параметров, которые будут делать данные «наиболее приближенные» к реальным. Метод максимального правдоподобия является уникальным и простым способом определения решения при нормальном распределении.

Метод наибольшего правдоподобия используются во многих статистических моделях:

В линейных и обобщенных линейных моделях;
В факторном анализе;
При моделировании структурных уравнений;
Во многих ситуациях, предполагающих проверку гипотезу и доверительный интервал формирования;
В дискретных моделях выбора и т.д.

Метод наибольшего правдоподобия заключается в том, что оценкой вектора неизвестных параметров

Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ

Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ

который доставляет максимум функции правдоподобия:

Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ

Иными словами, сущность метода наибольшего правдоподобия заключается в нахождении такого вектора параметров, при котором была бы наиболее вероятной реализация $x_1, … ,x_n$ случайной выборки $X_1,…, X_n$.

Точечные оценки, получаемые при методе наибольшего правдоподобия, носят название МП-оценки.

Видео:Как использовать метод максимального правдоподобия? Душкин объяснитСкачать

Пример использования метода максимального правдоподобия

Пусть необходимо найти при помощи метода максимально правдоподобия оценку заданного параметра p биноминального распределения

Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ

если в $n_1$ независимых испытания некоторое событие $A$ появлялось $m_1$ раз, а в $n_2 – m_2$ раз.

Для того, чтобы решить данную задачу, необходимо составить функцию правдоподобия:

Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ

Затем следует отыскать логарифмическую функцию:

Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ

На следующем этапе определяется первая производная p:

Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ

Найденную производную необходимо приравнять к нулю, тем самым записав уравнение правдоподобия.

Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ

После относительного решения полученного уравнения находим значение критической точки:

Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ

В данной точке вторая производная будет отрицательной, а, следовательно, данная точка является максимумом. Таким образом найденная точка принимается в качестве оценки по методу максимального правдоподобия неизвестной вероятности p биноминального распределения.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 23.07.2021