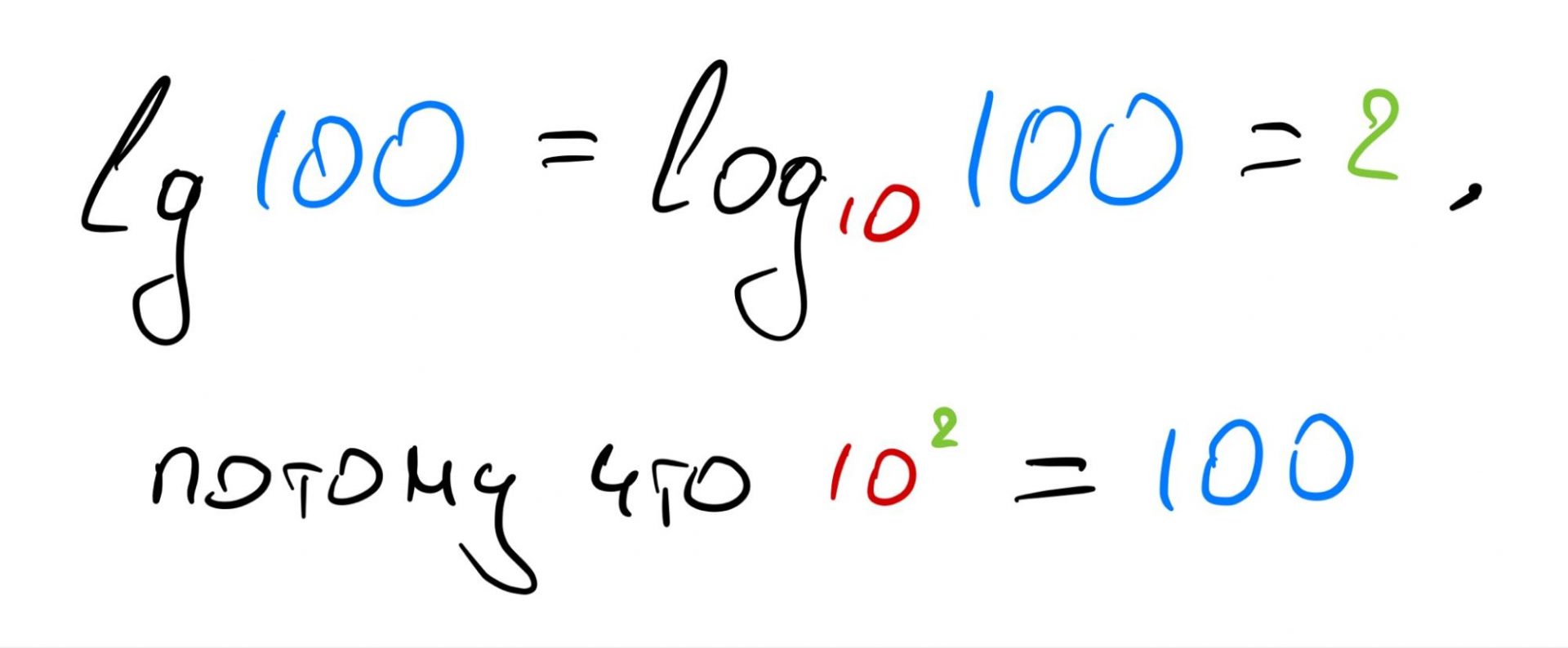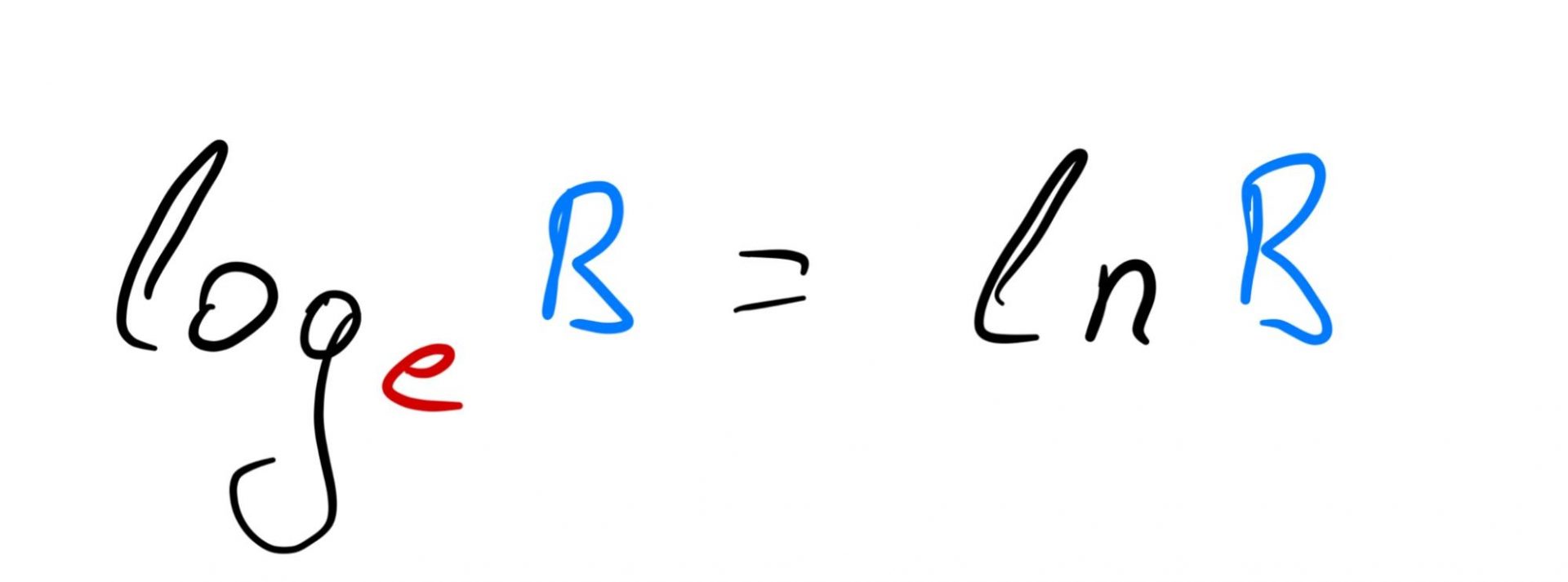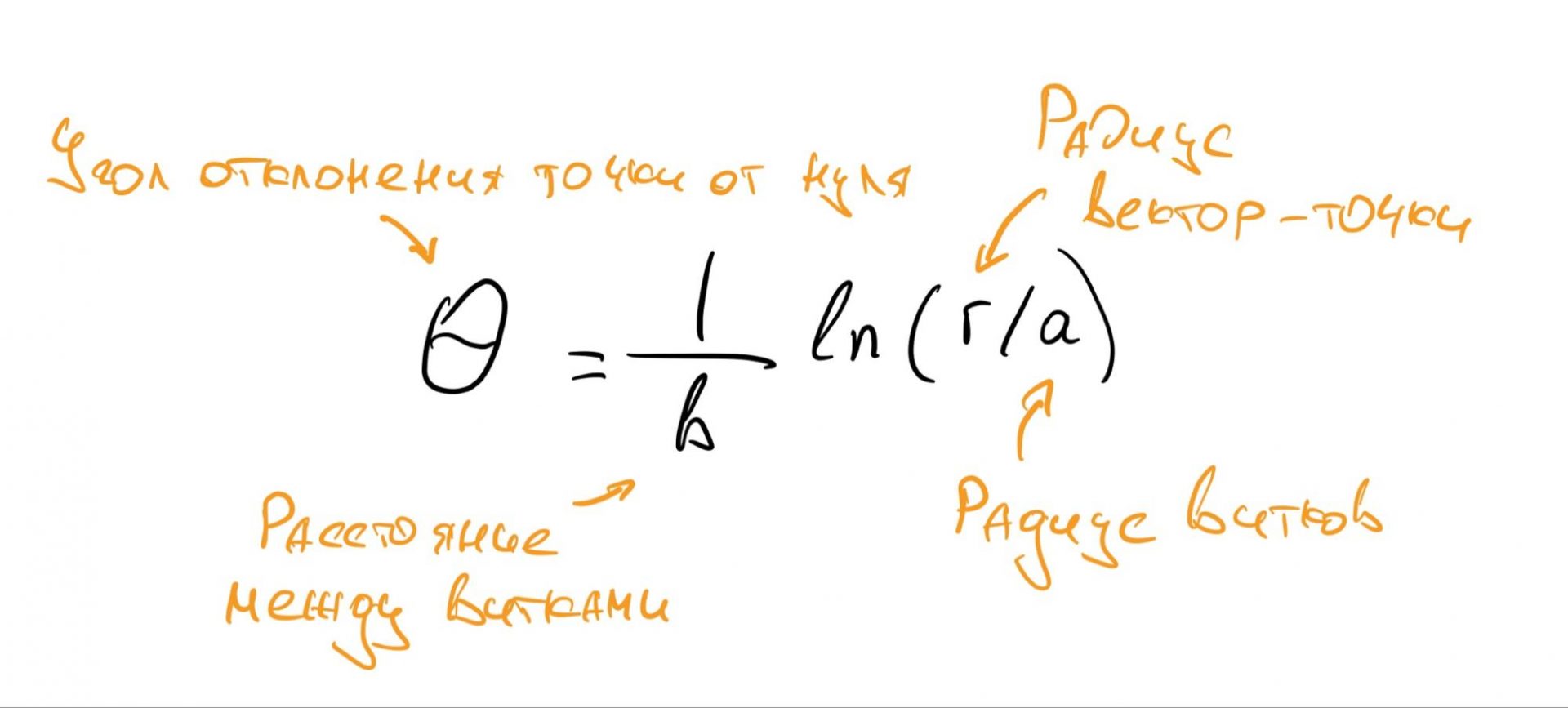Применение логарифмических уравнений в жизни

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Применение логарифмических уравнений в жизни

d10 = 2 * math.pi * a**2

print(‘площадь поверхности рассматриваемой планеты равна ‘, d11).

Правдивость данной расчетной программы была проверена на примере планеты Венеры путем ввода в программу ее данных. Программа показала высокую точность и верность вычислений (см. приложение 2 )

Формулы помогают нам найти нужные значения, но для полного понимания сути существования логарифмов следует найти и изучить более наглядный материал. Навигация для этого самый лучший вариант.

Локсодромия – линия на сфере, которая пересекает под одинаковым углом меридианы. Другими словами это кривая, в каждой точке имеющая путевой угол

С использованием в навигации магнитных компасов стало зарождаться понятие локсодромии. Простой пример: самолет летит с постоянным курсом относительно меридиана, над которым пролетает, и если магнитное склонение нулевое и нет ветра, то самолет в этой ситуации осуществляет движение по линии локсодромии.

Уравнение локсодромии выглядит следующим образом: , где – постоянные для данной локсодромии величины. Для того чтобы найти долготу нужно подставить в правую часть равенства соответствующую ей широту . Локсодромия — не единственная область навигации, использующая логарифмы в своих вычислениях. Однако в данной работе будет рассмотрена только она.

По определению локсодромии можно понять, что она представляет собой логарифмическую спираль на сфере, которая асимптотически приближается к полюсам, но никогда не пересекает их.

Итогом была проведена практическая работа по построению логарифмической спирали различными способами. В приложении 3 показана спираль, построенная путем заложения в основу программы GeoGebra уравнения логарифмической спирали в полярных координатах ( ). В приложении 4 представлена логарифмическая спираль, построенная с помощью прямоугольников, стороны которых имеют определенное отношение. Длины их сторон представлены числовым рядом Фибоначчи. Такая же работа была проведена вручную.

Громкость звука измеряют в децибелах, которые пропорциональны логарифму мощности звука, воздействующего на ухо. Употребление логарифмических шкал продиктовано особенностями наших органов чувств: зрения, слуха и т.д. Человеческий мозг воспринимает раздражения от органов чувств не пропорционально силе раздражителя (как мы рассматривали мощность звука), а лишь пропорционально ее логарифму. Именно поэтому ухо одинаково способно слышать шорох листьев и не оглохнуть от громкого удара станка на заводе. А глаз может заметить, как блестит снег на свету и не ослепнуть, если посмотрит на Солнце, которое в миллиарды раз ярче.

Описанные выше сведения объединяются законом психофизики, установленным Фехнером, который говорит, что мера ощущения пропорциональная логарифму величины раздражения.

Тот факт, что логарифмическая шкала позволяет увидеть и осознать объекты большого масштаба позволяет применять понятие логарифма и в истории. Чтобы представить себе всю эволюцию нашего человечества нужно представить его историю в масштабе, который подвластен представлению. В этом на помощь приходит логарифмический масштаб (шкала). Такая система называется логарифмической шкалой времени.

Из этого следует, что логарифмы применимы в математическом моделировании развития мира, культуры, экономики и так далее.

То, какое значение логарифм имеет в физике, является отдельной темой для проекта по количеству материала, имеющегося по этому направлению. Здесь будет рассмотрена только одна формула – формула Циолковского.

Формула Циолковского значительно выделяется на фоне всех приведенных в этой работе расчетов. Это достижение было важным для истории тем, что открыло новую эпоху в сфере естествознания и космонавтики. Формула предназначена для того, чтобы рассчитывать характеристическую скорость летательного аппарата, т.е. скорость которую он приобретает под действием тяги двигателя, не имея воздействия со стороны других сил. Эта формула приобретает соответствующий вид в зависимости от вида самого рассматриваемого аппарата. Речь идет о количестве ступень ракеты. Для ракет с 2-мя, 3-мя ступенями действительная более сложная формула, которая не рассматривается в данной работе. Для ракет с 1-ой ступенью используется формула более простого вида: . Где – удельный импульс ракетного двигателя, – начальная масса РН (ракета-носителя), включающая в себя массу полезной нагрузки, самого аппарата и топлива на момент старта, – «сухая масса», т.е. масса полезной нагрузки и аппарата. На данный момент существует одна ракета подобного вида, разрабатываемая в России, обладающая одной ступенью. Она называется РН «Корона» и разрабатывается уже на протяжении 25 лет. Данные необходимые для подстановки были взяты из характеристик этого ракета-носителя и написана соответствующая программа. Результаты смотрите в приложении 5.

5. Незамысловатый фокус

Представьте, что в ваш город приехал фокусник, утверждающий, что может с легкостью вычислить корень высокой степени из многозначного числа. Перед представлением вы заготовили 31-ю степень какого-нибудь многозначного числа и в итоге получили пятизначное. Уверенные в том, что фокусник не сможет извлечь из него корень вы начинаете говорить «31-ая степень этого числа : пятизначное число …» и тут произошло чудо, этот волшебник уже написал вам ответ на доске, даже не услышав само число. Как так вышло?

На самом деле здесь нет ничего сложного. Есть только одно число, которое в 31-й степени дает пятизначное число. Однако даже если так, то откуда тот фокусник знал это и смог так быстро отыскать нужное число?

Для этого он заучил двузначные логарифмы для первых 15-20 чисел. Тем более эта задача сильно упрощается знанием того факта, что зная логарифмы 2,3 и 7, можно в уме легко найти логарифмы чисел первого десятка ( ).

Когда вы сказали фокуснику, что 31-ая степень числа дает пятизначное число, ему оставалось только выполнить следующее действие: . Значение этого выражения лежит где-то между 1,09 и 1,13. Этот интервал включает в себя только один логарифм от целого числа. Это 1,11 – логарифм числа 13. Конечно, чтобы такое проделать в уме нужна тренировка, но если видеть это все перед глазами, то все довольно просто.

Теперь уже перед вами стоит задача извлечь корень 64 степени из 20-значного числа. Получим: То есть значение лежит в интервале между или по-другому между 0,29 и 0,31. Такое значение только одно 0,3 – логарифм числа 2.

Использование логарифмов дает людям преимущество в виде упрощения и ускорения сложных вычислительных операций. Бесспорно, будет нерационально использовать это при умножении 6 на 3, но при действиях с по-настоящему большими числами данное преимущество значительно упростит задачу.

Логарифмическая функция дает нам возможность по-другому взглянуть на масштабные процессы, происходящие в огромных пространствах и временных интервалах для понимания и осмысления общей картины.

В ходе работы поставленные задачи были выполнены, гипотеза подтверждена, проработана практическая часть и цель достигнута.

1. . Вильчек Ф. Красота физики: постигая устройство природы: пер. с англ. – 2-е изд. – М.: Альпина нон-фикшн, 2017.

2. Выгодский М.Я. Справочник по элементарной математике – Москва: Издательство: АСТ: 2017

3.Засов А.В., Постнов К.А. Общая астрофизика – Фрязино: Век 2: 2015

4 Перельман Я.И. Занимательная алгебра. – СПб.: СЗКЭО, 2017

5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов – Москва: государственное издательство физико-математической литературы, 1963

6. Энциклопедия для детей: Т.8. Астрономия. – 2-е изд., глав.ред. М.Д.Аксенова – М.: Аванта+, 1999

7. https://ru.wikipedia.org – Википедия, Свободная Энциклопедия

Приложение 1. Звездные величины. Расчет.

Приложение 2. Площадь планеты. Расчет и проверка.

(взято с википедии)

Приложение 3. Логарифмическая спираль

Приложение 4. Логарифмическая спираль

Приложение 5. Формула Циолковского. Расчет и проверка.

Видео:Наглядно показываю, зачем нужны логарифмы в жизниСкачать

Что такое логарифм в математике и в жизни

И при чём здесь капуста, горные козлы и ракетостроение

Для многих логарифм — это самая странная часть в математике: непонятно, как их считать, где применять и как они могут пригодиться в жизни. Сегодня ответим на все эти вопросы.

Если интересно, как в математике работают остальные функции и символы, вот что у нас уже есть:

Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать

Что такое логарифм

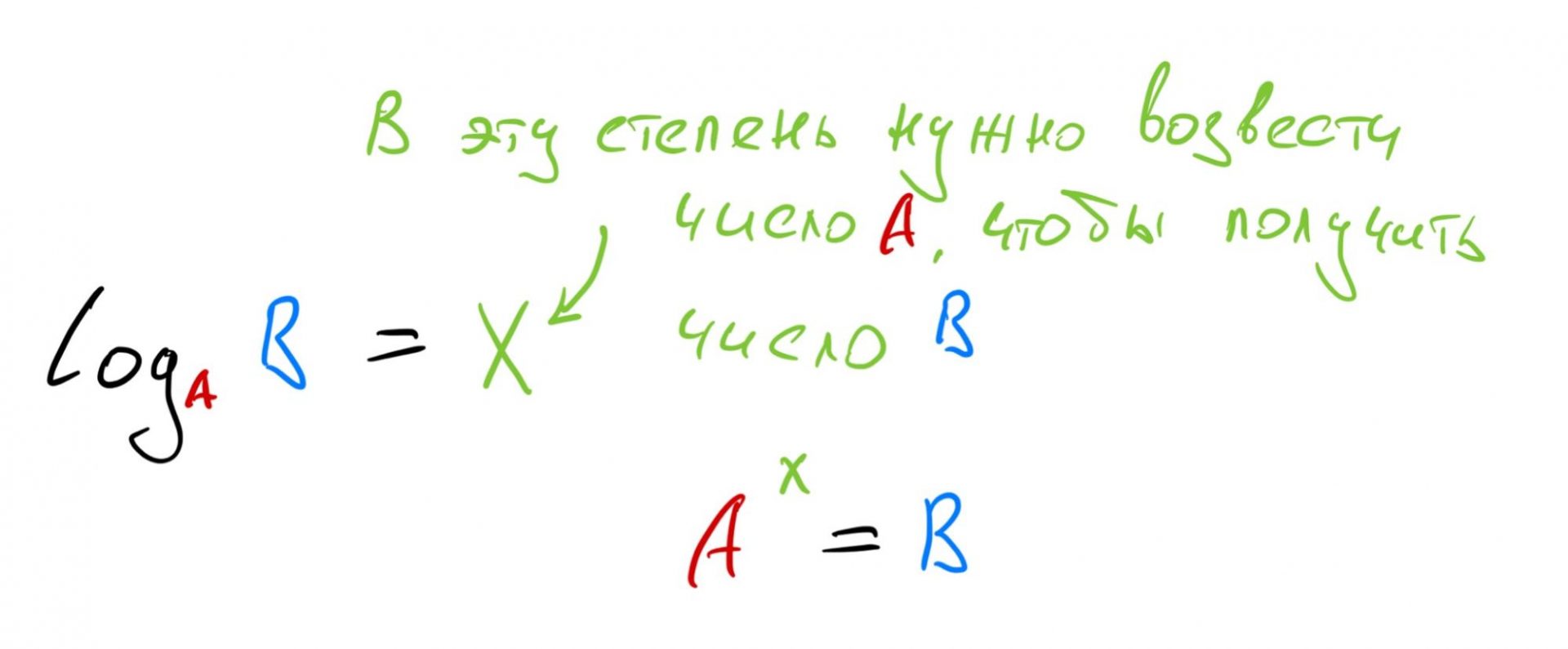
Задача логарифма — ответить на такой вопрос:

В какую степень нужно возвести одно число, чтобы получилось другое?

На языке математики это будет выглядеть вот так:

Теперь сделаем то же самое, но уже с числами. Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.

Видео:Логарифмические уравнения. 11 класс.Скачать

Десятичный, натуральный и другие логарифмы

Число A, которое возводят в какую-то степень, называется основанием логарифма. Самые популярные у математиков логарифмы — десятичный и натуральный.

Десятичный логарифм — это когда в основании логарифма стоит число 10. Наша задача в этом случае — найти, в какую степень нужно возвести 10, чтобы получить желаемое число. Обозначается так — lg:

Натуральный логарифм устроен похоже, только вместо десятки в основании логарифма стоит число e, которое примерно равно 2,71828 и называется числом Эйлера. В математике число e играет такую же важную роль, как в геометрии — число пи, поэтому логарифм по основанию e часто встречается во многих математических выкладках и доказательствах.

Обозначается натуральный логарифм так — ln:

Видео:Решение логарифмических уравнений #shortsСкачать

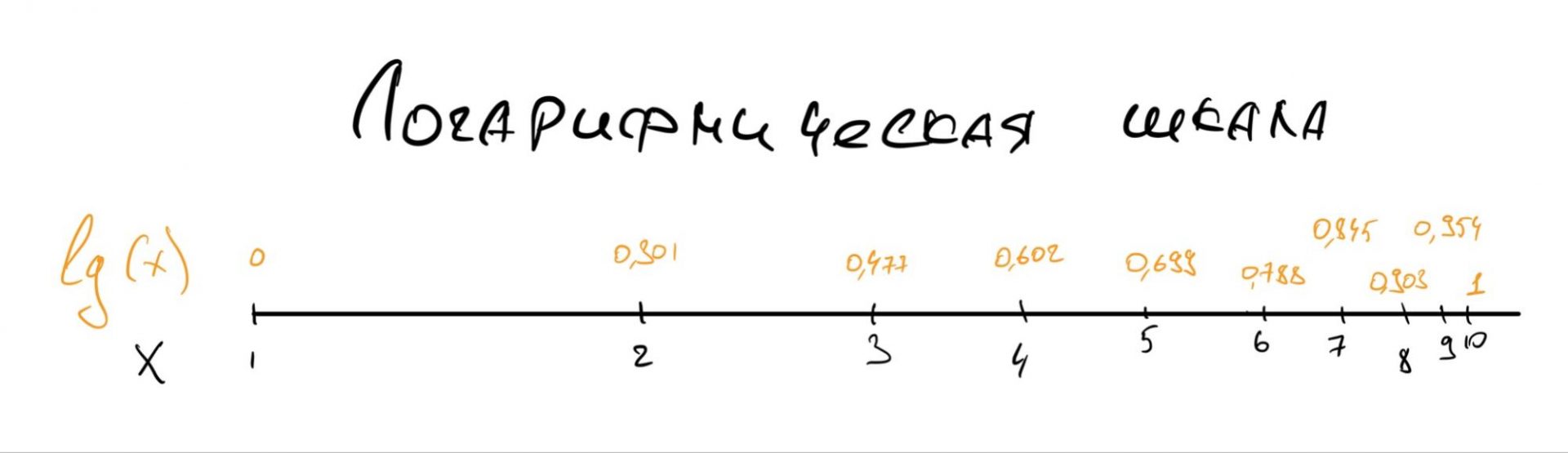
Логарифмическая шкала

Если мы возьмём линию и отметим на ней точки через каждый сантиметр, то мы получим арифметическую шкалу. Арифметическую — потому что каждая новая отметка считается арифметическим действием — сложением шага и предыдущего значения:

Но если мы вместо сложения возьмём логарифм, например, по основанию 10, то каждая новая отметка будет зависеть от значения десятичного логарифма:

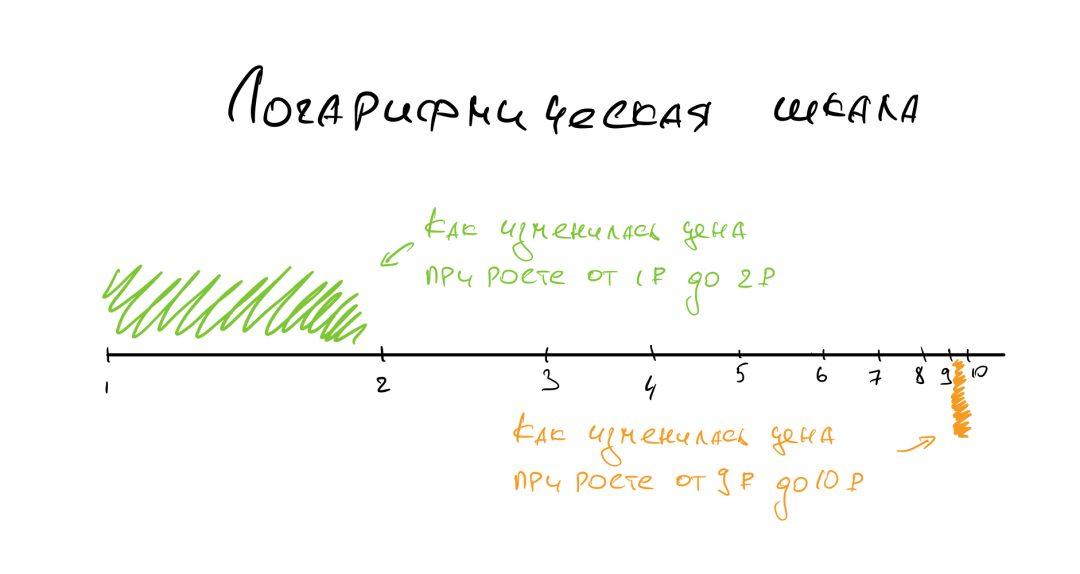
Это выглядит странно, но логарифмическая шкала постоянно применяется в экономике и маркетинге, когда нужно оценить рост или падение стоимости товара. Если взять обычную арифметическую шкалу, то разница между парами (1, 2) и (9, 10) будет одной и той же — 1 пункт.

Но при этом в первом случае цена выросла в 2 раза, с 1 до 2, а во втором случае — всего лишь на 10%. С логарифмической шкалой рост цены будет выглядеть логичнее:

Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Зачем нужны логарифмы в жизни

Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется. Вот несколько примеров.

Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.

В химии активность водородных ионов тоже считается по логарифмической шкале.

Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.

В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.

Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Логарифмы в природе

Больше всего логарифмов можно встретить в природе в виде логарифмической спирали. Математическая формула спирали выглядит так:

Если мы захотим построить график этого уравнения, то он будет выглядеть так:

Логарифмическая спираль в математике.

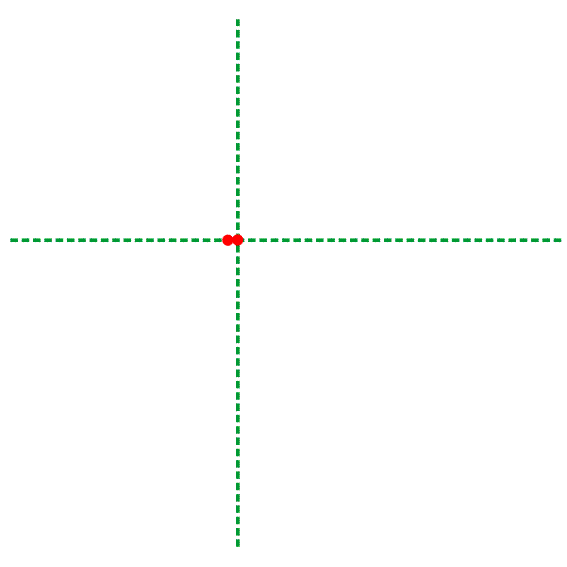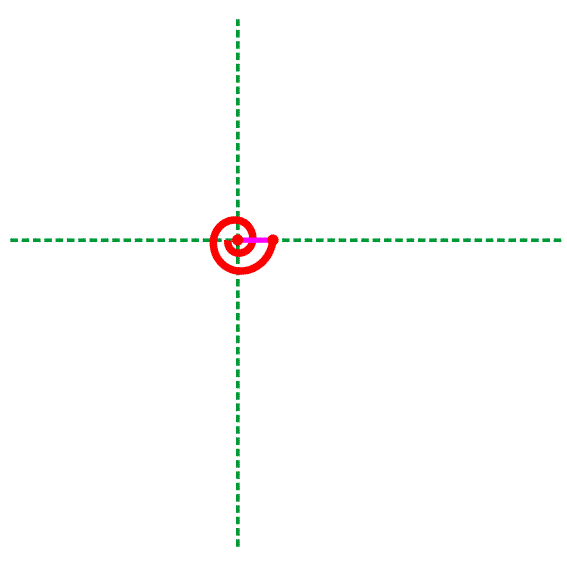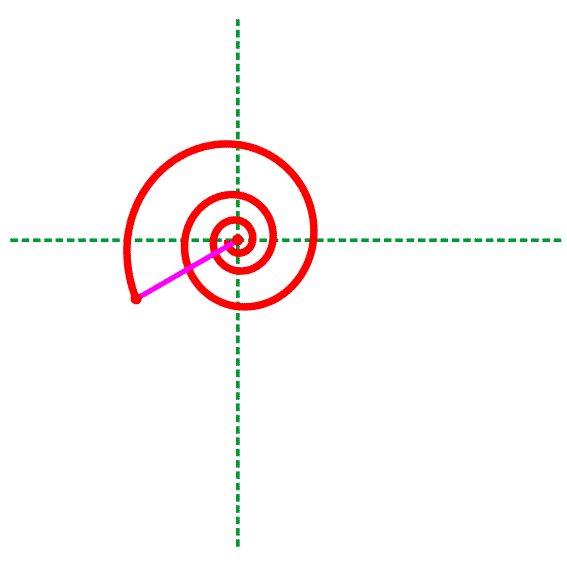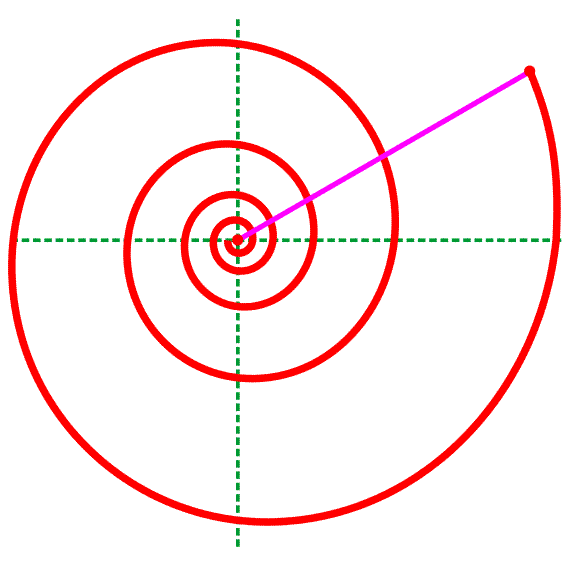
А вот логарифмическая спираль в природе — в ракушках, подсолнечнике и капусте. С капустой ещё связана другая интересная тема — фракталы, но про них поговорим в другой раз.

Даже рога у горных козлов закручиваются по логарифмической спирали:

Видео:Умножаем логарифмы В УМЕ🧠Скачать

Что дальше

Теперь мы знаем про логарифмы достаточно, чтобы понять, как они работают. В следующей статье напишем простую программу из двух циклов, которая посчитает нам практически любой логарифм по любому основанию.

Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Исследовательская работа на тему «Логарифмы, их практическое применение в жизни человека»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ПРИМОРСКОГО КРАЯ

ФИЛИАЛ КРАЕВОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

«УССУРИЙСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ»

В ХАНКАЙСКОМ РАЙОНЕ

Логарифмы, их практическое применение в жизни человека.

Выполнил: Студент гр. 121, Автомеханик

Ефименко Андрей Алексеевич

Руководитель: Гуржий Валентина Ивановна

Ханкайский район, с. Камень-Рыболов.

Тему «Логарифмы» мы изучали на первом курсе. Изучение темы начиналось с определения логарифма.

Определение. Логарифмом положительного числа b по основанию a, где a › 0, a ≠1, называется показатель степени, в которую надо возвести число a, чтобы получить число b.

а х = b т.е. log _а b = х

Студентам логарифм казался сложным понятием и никому не нужным.

Меня заинтересовала эта проблема. И я решил провести исследование показать необходимость изучения логарифмов и найти их применение в жизни человека.

Объекты исследования : логарифмы и логарифмическая функция.

Предмет исследования : история возникновения и развития логарифмов, логарифмических функций и их практическое применение в жизни человека.

Проблема: известно, что логарифмы и логарифмические функции изучаются студентами на занятиях по математике на 1 курсе, о его широком применении нет полной информации.

Мне стало интересно узнать о более широком применении логарифмов в сферах человеческой деятельности.

И ответить на возникший вопрос: «Для чего нужны логарифмы, являются ли они жизненной необходимостью?»

Гипотеза : Если в математике существует теория логарифмов, то существующая теория должна где-то найти применение.

Цель: доказать, что существует практическое применение логарифмов в жизни человека, убедиться в их значимости в жизни человека.

Найти и изучить материал по истории возникновения логарифмов.

Проанализировать, где в природе встречаются логарифмы.

3.Проанализировать, в каких сферах жизни человека применяются логарифмы.

4.Сделать соответствующие выводы по исследовательской работе.

Актуальность: На уроках математики мы встречались с термином «Логарифм», но мало что знали о практической значимости этого понятия в жизни человека.

И я решил способствовать развитию познавательного интереса, узнать как можно больше об истории развития логарифмов, доказать значимость их применения в жизни человека.

Планируемый результат: Расширить представление о логарифмах, убедиться в их практической значимости в жизни человека.

2. Основная часть

2.1 История логарифма

Во все времена человечество пыталось вычисления упростить, составлялись таблицы, формулы для приближённых вычислений, которые заменили бы сложные операции вычислений на более простые вычисления. Потребность в новом способе счёта возникла в 16 веке, так как в это время развивается астрономия, торговля.

В это время, в эпоху Возрождения усиленно развивается судоходство, крупнейшие европейские державы стремятся к владычеству на море, происходят мореплавания на большие расстояния.

Обработка полученных данных требовала колоссальных расчетов, и, следовательно, стали необходимы новые средства упрощения вычислений. Такими средствами в 15 — 16 веках явились в первую очередь логарифмы и десятичные дроби. Логарифмы также были созданы в 16 веке как средство для упрощения вычислений. В их основе лежит очень простая идея, знакомство с которой приписывается еще Архимеду.

Ученые приходят к выводу, что если заменить умножение и деление на сложение и вычитание, то сложности астрономических вычислений сократятся. Была сопоставлена геометрическая прогрессия с арифметической, при том, что геометрическая – исходная.

При этом упрощалось не только умножение и деление, но и извлечение корня п-ой степени, преобразуется в деление логарифма подкоренного выражения на степень п.

Вся эта теория принадлежит Михаэлю Штифелю. Так считают, потому что он был первым, кто опубликовал ее в своей книге.

В 1614 году выходит книга шотландца Джона Непера на латинском языке опубликованная в Эдинбурге, сочинение под названием « Описание удивительной таблицы логарифмов». В этой книге он даёт краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′.

Сочинение « Описание удивительной таблицы логарифмов» было разделено на 2 книги, из которых первая книга посвящена логарифмам, а вторая книга тригонометрии.

Понятия функции тогда ещё не существовало, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M , где M — масштабный множитель. Непер = 10000000.

В то время все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Но и это не помешало новой методике вычислений получить широчайшую популярность.

Многие европейские математики, включая Кеплера, стали составлять логарифмические таблицы.

В это время математик – Бригг, который восхищался Непером, за то, что тот открыл такую гениальную вещь как логарифм. Бриг поехал в Шотландию, чтобы увидеть изобретения и сделал открытие десятичных логарифмов.

Так логарифмы стали применяться практически во всех сферах жизни. Там, где нужно было проводить вычисление над многозначными числами или где была необходима точность до 5-ого знака после запятой стали применять логарифмы. На практике более точные результаты не используются. Учёные убедились, что логарифмы уникальны, способны описать практически любое физическое явление.

Первые десятичные логарифмы появились в 1615 году и были напечатаны первые логарифмические таблицы.

Непер тогда предложил взять за логарифм единицы нуль, а за логарифм десяти — 100, или, что сводится к тому же, просто 1.

Непер не смог усовершенствовать свои таблицы из-за болезни, однако дал Бригсу (1561-1631) рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617). Рисунок 1.

После появления логарифмов Непера, через несколько лет в 1620 г Эдмунд Уингейт и Уильям Отред изобрели незаменимый счётный прибор – логарифмическую линейку. Умножение и деление чисел на логарифмической линейке заменяется соответственно сложением и вычитанием их логарифмов. Учёные, инженеры, астрономы с помощью логарифмической линейки смогли быстро получать ответ в три значащие цифры с достаточной точностью. Рисунок 2.

Рисунок 2.

Логарифмические линейки использовались до начала 1980-х годов.

Первая логарифмическая линейка была незаменима до появления первых карманных калькуляторов.

И хотя теперь её вытеснили из обихода микрокалькуляторы, можно с уверенностью сказать, что без логарифмической линейки не были бы созданы первые компьютеры, калькуляторы.

Знаки log и Lg были введены в 1624 году И. Кеплером.

Термин «натуральный логарифм» ввели Менголи в 1659 г. и вслед за ним Н. Меркатор в 1668 г., лондонский учитель Джон Спейдел. издал таблицы натуральных логарифмов чисел от 1 до 1000 под названием «Новые логарифмы».

В 1703 году издаются первые логарифмические таблицы на русском языке.

С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов.

Прошло 394 года с тех пор, как логарифмы впервые были введены (считая с 1614 г.), прежде чем математики пришли к определению понятия логарифма, которое теперь положено в основу школьного курса математики. Возник вопрос, нужны ли сегодня логарифмы?

Из предыдущего мы узнали, что в 16 веке логарифмы нужны были как средство для упрощения вычислений. В настоящее время, когда вычислительная техника настолько совершенна, чтобы справиться с самыми сложными расчётами, так зачем изучать логарифмы сегодня?

Однако и в XX I веке логарифмическая линейка нашла своё применение в наручных часах, т.е. получила своё второе рождение. Рисунок 3.

Следуя моде производители модных дорогих часов с электронным хронометром и ЖК экранами перешли к стрелочным, и места для того чтобы встроить калькулятор, оказалось недостаточно.

Спрос людей, следящих за модой и желающих приобрести хронометры со встроенным вычислительным устройством увеличивалось, и производители выпустили новую модель часов круглой формы с встроенной логарифмической линейкой.

Такие устройства производители назвали «навигационная линейка». В чём их достоинство, они дают возможность получать информацию, например, рассчитать таблицу расхода топлива на пройденное расстояние, посчитать пульс, определить скорость электропоезда, которая равна соответствующей табличной форме.

Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

2.2 Логарифмическая спираль.

Почему логарифмическая спираль является примером логарифмической зависимости в природе и не только? Попробую ответить на этот интересующий нас вопрос. Во-первых, логарифмы и сегодня позволяют упрощать вычисления.

Во-вторых, всегда, во все времена цель математической науки, остаётся одной, помочь людям узнать больше об окружающем мире, познать его тайны и закономерности.

Многие явления природы помогает описать логарифмическая зависимость, т.е. логарифмическая функция. Математики, пытаясь составить математическую модель того или иного явления, стали часто обращаться к логарифмической функции. Ярким примером этого обращения является логарифмическая спираль. Рисунок 4.

Логарифмическая спираль – плоские линии в геометрии, которые отличаются от прямых и окружностей и скользят сами по себе.

Эта логарифмическая спираль закручивается вокруг полюса, стремится к нему, но не достигает, а в другую сторону до бесконечности развёртывается.

Логарифмическая спираль явилась ярким примером логарифмической зависимости в природе, а почему? Постараюсь найти объяснение этому.

По правилам природы, все живые существа растут во всех направлениях, сохраняя общие начертания своей формы. Взрослое существо всегда выше и толще детёныша. Однако раковины морских животных растут лишь в одном направлении. Рисунок 5.

И чтобы не вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие первоначальной формы раковины.

А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога горных козлов закручены по логарифмической спирали. Рисунок 6.

Логарифмическая спираль является математическим символом соотношения формы и роста. Немецкий поэт Иоганн-Вольфганг Гете считал эту спираль математическим символом духовного развития и жизни.

По логарифмической спирали очерчены не только раковины. По логарифмическим спиралям закручивает нити вокруг центра один из распространенных пауков, Эпейра, таким образом, сплетая паутину. Рисунок 7.

Семечки в подсолнухе располагаются по линиям, напоминающим логарифмическую спираль. Рисунок 8.

По логарифмическим спиралям закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система.

Вопрос логарифмических линий в природе не остался без внимания не только математиков, но и художников. Один из известных художников того времени Сальвадора Дали 18 декабря 1955г. вынес на повестку своего публичного выступления, которое проходило в Париже, в главной аудитории Сорбонны вопрос о замечательных логарифмических линиях. Вот небольшие отрывки из его выступлений.

«…моей навязчивой идеей, настоящей маниакальной страстью, стала картина Вермера «Кружевница», репродукция которой висела в отцовском кабинете. Рисунок 9.

« Уже много лет спустя я попросил в Лувре разрешение написать копию с этой картины. Потом я попросил киномеханика показать на экране репродукцию нарисованной моей копии… Я объяснил, что, пока не написал копию, в сущности, почти ничего не понимал в «Кружевнице», и мне понадобилось размышлять над этим вопросом целое лето, чтобы осознать наконец, что я инстинктивно провел на холсте строгие логарифмические кривые…»

«Одновременно с этим я углубил свои исследования по морфологии подсолнуха – по вопросу, по которому в свое время сделал чрезвычайно интересные выводы еще Леонардо да Винчи. Никогда еще в природе не существовало столь совершенного примера логарифмических спиралей…»

Вот некоторые удивительные свойства логарифмической спирали:

1.При преобразовании подобия логарифмическая спираль остается неизменной. Это свойство так удивило изучавшего ее Якоба Бернулли ( XVII в.), что он придал им мистический смысл.

2. Логарифмическая спираль пересекает свои радиус-векторы под постоянным углом, поэтому её называют равноугольной.

3.Третье свойство. Свойство логарифмической спирали пересекать все свои радиус-векторы под одним углом, даёт возможность её применения в технике.

В технике часто применяются вращающиеся ножи. Сила давления ножей на разрезаемый ими материал, зависит от направления скорости вращения и угла между лезвием ножа. Чтобы давление удержать постоянным, нужно сохранить постоянное значение угла резания, а это возможно, если лезвия ножей имеют форму дуги логарифмической спирали. Рисунок 10.

Величина угла резания зависит от материала, из которого изготовлен нож. По логарифмической спирали изгибают трубу, которая приводит поток воды к лопастям турбины. Благодаря форме логарифмической спирали, потери энергии на изменение течения воды в трубе становятся, минимальными, а напор воды становится, максимальным. Рисунок 11.

2.3 Логарифмы в сельском хозяйстве.

Поскольку мы живём в сельской местности, захотелось узнать, где применяются логарифмы в сельском хозяйстве? Из дополнительной литературы я узнал, что есть формула m = m ₀ ∙ e kt , по которой происходит рост животных, и можно узнать относительную скорость роста, где m -масса животного в полмесяца, m ₀ – масса при рождении, e — экспонента, k — коэффициент относительной скорости роста, t –период времени. Рисунок 12.

Приведу пример своего расчёта, используя данную формулу.

Новорожденный бычок имел массу 27,2 кг, через полмесяца он подрос, набрал массу уже до 41кг. Узнаю, какой масса будет в возрасте одного месяца. Нахожу относительную скорость роста, используем формулу: m = m ₀ ∙ e kt ; 41= 27,2 e k 0,5 ;

lg 41= lg 27,2 + 0,5 k ∙ lg e , 1,6128 =1,4346 +0,5 k ∙0,4343; k =0,821 теперь легко определить массу в возрасте одного месяца:

m =27,2∙ e 0,821 ; lgm = lg 27,2+0,821 lge =1,4346 + 0,821∙0,4343 =1,7912; m =58,4 (кг.)

Работая над темой, я раскрыл для себя много интересного, полезного.

Я ещё раз убедился, что своё применение логарифмы нашли в сельском хозяйстве на ферме для животных.

Чтобы рассчитать сколько нужно корма для поддержки организма на работу внутренних органов, теплоотдачу, на восстановление отмирающих клеток и т.д., которое происходит пропорционально внешней поверхности тела животных.

Например, нужно определить калорийность такого корма для быка, весящего 320кг, если мы знаем, что бык весом 530кг тратит при этих условиях 11360 калорий.

Для решения этой задачи приходит и геометрия: т.к. по условию задачи сказано, что калорийность пропорциональна поверхности быка

х : 11360 = s : s ₁ , где S ₁ — поверхность тела быка, который весит 530кг. т.е. =

Из геометрии мы знаем, что поверхности (s) подобных тел относятся, как квадраты их линейных размеров, а объемы (и, следовательно, веса) — как кубы линейных размеров. Поэтому = ;т.е. = ; = = ;

х = 11360∙; используя логарифмические таблицы, находим х =12300 Быку необходимо 12300 калорий.

Что объединяет шум и звёзды?

Я узнал, что громкость шума и яркость звёзд оцениваются по логарифмической шкале. Применение логарифмических шкал рекомендовано особенностями наших органов чувств: зрения, слуха и т.д. Рисунок 13.

Со времен древнегреческого астронома Гиппарха ( II в. до н.э.) используется понятие «звездная величина». В те времена считали, что расстояния до звёзд одинаковы и что чем она ярче, тем звезда больше.

Астрономы разделили звёзды на светила первой величины 1 T , а величины едва различимые глазом к шестой 6 T в зависимости от степени видимой яркости.

Блеск звезды 1 T в 100раз больше звезды в 6 T , а это означает, что разность в 5 звёздных величин ровно в 100 раз соответствует различию в блеске.

Я узнал, что звёздная величина характеризуется не размерами звезды, а её блеском, т.е. освещенностью, которая создается на Земле.

Так как звёзды находятся на разных расстояниях, их видимые звёздные величины не говорят о мощности излучения звёзд, в астрономии, кроме понятия «видимая звёздная величина» появилось понятие абсолютные звёздные величины.

«Величина» звезды является не что иное, как логарифм ее физической яркости.

Я узнал, что работая над оцениванием яркости звёзд, астрономы пользуются таблицами логарифмов по основанию 2,5. Как происходит оценивание громкости шума?

Единицей громкости служит «бел», практически – его десятая доля, «децибел».

Для слуха человека степени громкости 10 децибел, 20 децибел и т.д. составляют геометрическую прогрессию.

Однако объективная (физическая) сила шумов является геометрической прогрессией со знаменателем 10.

Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы. Рассмотрим несколько примеров.

Тихий шелест листьев деревьев оценивается в 1 бел, громкая разговорная речь — в 6,5 бела, рычанье зверя — в 8,6 бела. Получаем, что сила звука разговорной речи громче шелеста листьев деревьев.

106,5-1 = 105,5 = 316000 раз; рычанье зверя сильнее громкой разговорной речи в 108,6-6,5 = 102,1 = 158 раз.

Вредным для человеческого организма считается шум громкостью больше 8 бел.

При оценке видимой яркости светил и при измерении громкости шума, мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения. Оказывается, что оба эти явления–следствие общего психофизического закона Вебера-Фехнера, согласно которому ощущение изменяется пропорционально логарифму раздражения. Рисунок 14.

Так я узнал, что логарифмы вторгаются и в область психологии.

Децибелы, измеряющие громкость звука, которые воздействуют на наши уши, пропорциональны логарифму мощности звука. Человеческий мозг в отличие от мощности звука воспринимает раздражения от органов чувств: зрения, слуха и т.д. пропорционально её логарифму, а не пропорционально силе раздражителя. Поэтому наши уши способны услышать шорох листьев деревьев и не оглохнуть от громкого звука. Глаза могут заметить, как сверкает снег на свету и не ослепнуть, смотря на солнце, которое ярче в миллиарды раз.

Логарифмы находят самое широкое применение и при обработке результатов тестирований в психологии и социологии.

Воспринимаемые органами чувств человека ощущения, могут отличаться во много миллионов, даже миллиардов раз друг от друга раздражениями. Удары молота о металлическую трубу в сто раз громче, чем тихий шелест листьев деревьев, а яркость вольтовой дуги в триллионы раз превышает яркость какой-нибудь звезды, едва видимой на ночном небе. Опыты показали, что организм человека как бы «логарифмирует» полученные раздражения, то есть величина ощущения приблизительно пропорциональна десятичному логарифму величины раздражения. Поэтому учёные выработали приём точной числовой оценки громкости шума, которую необходимо соблюдать во избежание вредного влияния промышленных шумов на здоровье рабочих и на производительность труда. Отсюда делаем вывод, что логарифмы и логарифмическая функция помогают человеку объяснить многие тайны природы человеческих ощущений.

Логарифмы в музыке.

Теперь рассмотрим еще один интереснейший пример о связи логарифмов и музыки. Рисунок 15.

Математикой музыканты редко увлекаются, но тем ни менее даже не подозревая, они с математикой встречаются и очень часто и притом с такими «странными» понятиями как логарифмы. Определённые закономерности являются основой музыкальной гаммы. Для создания гаммы удобно пользоваться логарифмами соответствующих частот: log 2w0, log 2w1.

lg N _pm = , N _pm – номер клавиши, m — номер октавы, p — номер звука в октаве делённый на 12.

Оказывается, нажимая на клавиши рояля, можно сказать, что музыкант играет на логарифмах. Действительно, так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношению к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. И основание этих логарифмов равно 2.

Номер клавишей есть логарифм числа колебаний соответствующих им звуков умноженные на 12.

Можно сказать, что номер октавы представляет, целую часть (характеристику) логарифма числа колебаний этого тона, а номер звука в данной октаве, деленный на 12 – дробную часть (мантиссу) этого логарифма.

Звездные галактики. Галактики, штормы и ураганы – впечатляющее применение логарифмов.

Галактика закручена по логарифмической спирали, и ей принадлежит солнечная система. Рисунок 16.

В 1845 году английский астроном Уильям Парсонс с помощью с помощью телескопа открыл класс туманностей в виде логарифмической спирали. Яркий пример тому является туманность в созвездии Гончих Псов. В первой половине XX столетия было установлено, что спиральные туманности – это звёздные системы, которые стали называть галактиками.

Чтобы описать с помощью логарифмов свойства спиральных галактик астрономам пришлось приложить много усилий. Галактики состоят из скоплений газа и горячих звёзд. И когда они вращаются, то распределяются вдоль ветвей логарифмической спирали.

В спиральных ветвях происходит повышение плотности, как звезд, так и межзвездного вещества – пыли и газа. У центра галактики ветви вращаются быстрее, повышенная плотность газа ускоряет образование и последующее сжатие газовых облаков и тем самым способствует рождению новых звезд. Поэтому спиральные ветви являются местом интенсивного звездообразования.

Молекула ДНК для каждой клетки нашего организма является ядром. Она представляет собой спираль, которая содержит генетический код жизни. Рисунок 17.

Молекулы ДНК, с точки зрения молекулярной теории, имеют огромную длину, которая состоит из двух нитей сплетённых в двойную спираль между собой. Эти нити сравниваются с нитями бус. Белки, которые также сравниваются с нитями бус, их «бусины» являются аминокислотами 20 различных типов.

У ДНК-всего 4 типа «бусин» и зовутся они нуклеотидами. «Бусины» двух нитей двойной спирали ДНК связаны между собой и строго соответствуют друг другу. Мы часто встречаем изготовление предметов по шаблону, называемому матрицей. Отливка монет или медалей, типографского шрифта. По аналогии происходящее в живой клетке восстановление двойной спирали по одной её цепи, как по матрице, так же называют матричным синтезом.

2.4 Применение логарифмов в различных сферах жизнедеятельности человека.

Математика вторгается в нашу современную жизнь с ее особым стилем мышления, становящимся сейчас обязательным и для инженера, и для биолога. Логарифмическая функция нашла применение и в биологии. Рисунок 18.

Логарифмы используются в биологии для описания явлений биологами. Процессы размножения микроорганизмов, рост колоний бактерий, радиоактивный распад элементов, изменение скоростей химических реакций и т.п.

Например, бактерия кишечной палочки в питательной среде каждую минуту делится.

Следовательно, общее количество бактерий каждую минуту становится в два раза больше.

То есть в начале процесса была одна бактерия, то через х минут их число N станет 2х, т.е. N (х) = 2х.

Пример. В начале процесса было 6 бактерий, через 2ч , после того как их поместили в питательную среду их число стало 100.

Через сколько времени сначала помещения бактерий в питательную среду возможно получить колонию 500 бактерий?

х=6, t =2, р = , в = 500. То есть требуемое время равно значению выражения 2∙ = ≈ 3,28, т.е. примерно через 3ч. 20мин.

Логарифмы нашли своё применение при расчёте звукоизоляции стен. Формула D = A ∙ Lg , где p – давление звука прошедшего через стену, p _{0 –} давление звука до поглощения, A — константа, которая равна 20 децибелам, позволяет определить коэффициент звукоизоляции стен. Например, если D — коэффициент звукоизоляции равен 20 децибел, тогда Lg =1, отсюда p ₀ =10 p , а это означает, что стена снижает звук в 10 раз. Такая изоляция у деревянной двери. Рисунок 19.

Радиоактивный распад. Формула m = m _{0 ∙} e ,где m ₀ начальная масса вещества в период времени t =0, m – масса вещества в момент времени t , помогает проследить, как изменяется масса радиоактивного вещества., T — период полураспада. Через время T масса радиоактивного вещества уменьшится в 2 раза после начального момента времени. Рисунок 20.

Формула Циолковского было важным достижением в истории того времени, т.к. открыла новую эпоху в области космонавтики.

Формула давала возможность рассчитывать характеристическую скорость летательного аппарата под действием тяги двигателя без воздействия сил со стороны.

V = V _{r ∙} ∙ Ln V _{r ∙} — означает скорость вылетающих газов, m ₀ – стартовая масса ракеты.

Формула позволяет связать скорость ракеты V с её массой m . При сгорании топлива V _r скорость истечения газа невелика. Логарифм растёт медленно, поэтому почти всю стартовую массу нужно отдать под топливо, чтобы отношение сделать большим и чтобы оно достигло космической скорости. Рисунок 21.

Изучив литературу, я узнал, что существует формула сложных процентов, которая нашла применение в банковском деле.

S _n = S ₀ (1 + ) n . Рисунок 22.

Например, вы положили в банк некоторую сумму денег. За то что деньги лежат в банке и банк ими пользуется, он за это начисляет р % годовых. И если деньги вы не снимаете, то положенная вами сумма S увеличивается за год и станет S ₁ , где S ₁ = S ₀ (1 + ).

S ₀ — начальная сумма, S ₁ — конечная сумма,

— процентная ставка

В конце n –ого года сумма вклада станет равной S _{n ,} которую посчитаем по формуле сложных процентов.

S _n = S ₀ (1 + ) n , тогда n = log∙( )

Например. Сколько потребуется лет, чтобы 100000 руб. выросли до 1000000 руб. при процентной ставке 20%, если деньги не снимали.

n = log ∙ ( ), считаем: n = log _(1+20/100) (1000000/100000) = 8.9 лет

Важно знать, что при процентной ставке больше, чем в 2,7 раза вклад, положенный под 100% годовых не увеличивается, если бы даже наросшие проценты начислялись каждую минуту, т.к. e = 2,7 используется в логарифмах как log _e x = lnx

В своей работе я постарался рассмотреть различные сферы практического применения логарифмов, показать, что их использование облегчает и сокращает сложные вычисления.

Мы знаем, что население Земли растет с каждым годом, и возникают проблемы с используемым пространством. Современные города в большинстве строятся без учёта будущего роста и впоследствии возникают пробки, загрязнения окружающей среды, снижение уровня здоровья населения.

Свойства логарифмической спирали нашло своё применение

и в архитектуре. Рисунок 23.

Можно строить города по принципу двойной логарифмической спирали. Примером служит самая красивая и современная столица Казахстана – Астана. Можно построить совершенно новый мегаполис в нашей стране, с красивыми микрорайонами в виде спирали, где могут находиться здания в виде логарифмической спирали или крыши зданий спроектированные в виде спиралей.

Вывод: Многие природные явления не могли быть изучены без понятия логарифма;

Логарифмы используются для описания природных явлений астрономами, физиками, биологами.

Понятие логарифма широко применяется человеком во многих науках.

Логарифмы на самом деле очень интересно изучать, если приводятся примеры из жизни. Оказывается, что логарифмы окружают нас в нашей жизни практически везде. Поэтому знание правил вычисления логарифмов и их свойств поможет разобраться во многих вопросах, которые ставит перед нами жизнь.

Результаты нашего исследования следующие:

1.Слова Галилео Галилея «Великая книга природы написана математическими символами» подтвердились в ходе работы над исследовательской работой;

2. Без понятия логарифма невозможно изучить многие природные явления;

3. Для описания многих природных явлений не только математики, но и учёные из области физики, биологии, астрономии, химии используют логарифмы для описания природных явлений;

4. Во многих науках человек применяет понятие логарифма;

5. Радиоактивный распад, изменение количества людей в стране, зависимость скорости ракеты от ее массы, коэффициент звукоизоляции и т.д. для их вычисления логарифм является инструментом.

Изучив, некоторые источники и дополнительную литературу, поставленные мной задачи были выполнены, я убедился, гипотеза подтверждена, цель достигнута. Математика есть в каждом предмете, она повсюду.

Я убедился, что логарифмы находят самое широкое применение и являются частью нашей жизни. Как уже мной было сказано, что цель математики помогать человеку, познать закономерности и тайны окружающего мира.

Логарифмы, в чём их преимущество, помогают сократить и упростить сложные вычислительные операции.

Логарифмы помогают определить раздражимость человека в определённой ситуации, люди, которые проживают в деревне и держат хозяйство, могут спокойно определить вес телёнка. Зная процент по вкладам, который предлагают банки, можно определить какой из них выгодный на данный момент.

По-другому взглянуть на процессы, которые происходят в огромных пространствах и временных интервалах даёт возможность для понимания и осмысления общей картины логарифмическая функция.

Использование логарифмов для удовлетворения практических нужд человека стало неотъемлемой частью нашей жизни.

Процессы размножения микроорганизмов, рост колоний бактерий, радиоактивный распад элементов, изменение скоростей химических реакций и т.п. имеют практическое применение логарифмов и показательной функции.

Итак, логарифмы имеют непосредственное отношение к физике, химии, биологии, экологии и многочисленным смежным наукам.

Как показало исследование, область применения логарифмов не ограничивается лишь техническими науками, она также играет важную роль в литературе, психологии.

С помощью их можно не только определить скорость летательного аппарата, рассчитать интенсивность звука, но и предсказать землетрясение, так как логарифмы являются основой физических и сейсмологических процессов. Величина, которая характеризует энергию, выделяющуюся, в виде сейсмических волн при землетрясении называется магнитудой землетрясения.

Итак, в результате исследования мы ещё раз убедились, что логарифмы появились исходя из практических нужд человека, и имеют непосредственное отношение многочисленным открытиям в различных областях науки.

В данной работе мною была рассмотрена тема «Применение логарифмов в различных сферах жизни человека», которая включает в себя вопросы об истории развития логарифмов, а также о логарифмической зависимости в окружающем нас мире.

Сведения, собранные мной в данной работе, — это далеко не всё, что можно рассказать о логарифмах в науках.

Использованная литература и источники

А.А.Колосов. Книга для внеклассного чтения по математике в старших классах (VIII – X) (издание второе, дополненное). Государственное учебно-педагогическое издательство Министерства просвещения РСФСР. Москва, 1963.

Райхмист Р.Б. Графики функций: Справ. пособие для вузов. – М.: Высш. шк., 1991. – 160 с.: ил.

Виленкин Н.Я. Функции в природе и технике: Кн. для внеклас. чтения IX – X кл. – 2-е изд., испр. – М.: Просвещение, 1985. – 192 с. – (Мир знаний).

Большая электронная энциклопедия «Кирилл и Мефодий»: 2004. Е.Я.Штейн «Большая школьная энциклопедия» том 1; Москва, 2004

М. Д. Аксенова. «Энциклопедия для детей». Том 11. Математика. – Аванта+, 2009

М.М. Лиман. Школьникам о математике и математиках. М.:Просвещение,1981;

📸 Видео

Математика это не ИсламСкачать

Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать

Интересная задача на логарифмы в ЕГЭСкачать

ЗАЧЕМ НУЖНЫ ЭТИ ... логарифмы! Математика на QWERTYСкачать

Проще простого! Как решить Логарифмическое Уравнение?Скачать

Решение логарифмических уравнений методом группировкиСкачать

84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Что такое Логарифмы? для ЧайниковСкачать

Логарифмическое уравнение / Как решить?Скачать

✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать