Видеоурок: Применение интегралов в физике и математике
Лекция: Примеры применения интеграла в физике и геометрии
Процесс нахождение первообразной называется интегрированием.
Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.
Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.
Итак, начнем сначала. Мы помним, что скорость – это первая производная перемещения. Но так как мы знаем, что интегрирование и нахождение производной – это два взаимообратных процесса, то мы можем предполагать, что, если для нахождения скорости, нужно было найти производную от перемещения, то для нахождения перемещения по скорости, необходимо произвести интегрирование заданной функции.
Отсюда можно сделать вывод, что перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:
Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:
По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].
Итак, найдем определенный интеграл данной функции:
Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.
Точно так же можно найти скорость по заданной функции ускорения.
Еще одной физической величиной, которая находится с помощью интегрирования, является работа.
Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:
Пример: Предположим, что к некоторому телу для его передвижения прикладывают силу, которая изменяется по закону F(x) = x +3. Необходимо найти работу, которую при этом совершает сила для перемещения тела с 1 м до 2 м.
Для нахождения работы следует найти определенный интеграл заданной функции по известным пределам интегрирования:
Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.
Кроме рассматриваемых задач, интегрирование в физике используется для нахождения работы по мощности, массы по плотности, заряда по силе тока, количества теплоты по известной теплоемкости, а также многое другое.
Что же касается геометрии, то геометрическим смыслом интегрирования считается нахождение площади фигуры под графиком.
Итак, чтобы найти площадь фигуры, которая ограничена с двух сторон пределами интегрирования и с одной стороны графиком функции, то необходимо найти интеграл данной функции:
Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х 2 на пределах рассмотрения х = 0, х = 4.
Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:
Видео:Простейшие интегральные уравненияСкачать

Решение задач физики и техники с применением интеграла
п.1. От ускорения к скорости и координате
Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).
п.2. Физические величины как интегралы других величин
Если (v(t)) — скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.
Скорость (v(t)=int a(t)dt)
Координата (x(t)=int v(t)dt)
Угловое ускорение (beta(t))
Угловая скорость (omega(t)=int beta(t) dt)
Угловая скорость (omega(t))
Угол поворота (varphi(t)=intomega(t)dt)
Скорость расходования горючего (u(t))
Масса горючего ракеты (m(t)=int u(t)dt)
Заряд (q(t)=int I(t)dt)
Работа (A(t)=int N(t)dt)
ЭДС индукции (varepsilon(t))
Магнитный поток (Ф(t)=-intvarepsilon(t)dt)
Скорость радиоактивного распада (I(t))
Число атомов радиоактивного вещества (N(t)=int I(t)dt)
Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_^F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.
В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow
cdot overrightarrowdt $$ где (overrightarrow
cdot overrightarrow) — скалярное произведение векторов импульса и скорости.
п.3. Примеры
Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin s(t)=int_^v(t)dt\ s=int_^(3t+2t^2)dt=left(frac+fracright)|_^=frac+frac-0=\ =3cdot 18+4cdot 36=54+144=198 text end
б) (v(t)=2(t+2)^, t_1=0, t_2=7) begin s=int_^2(t+2)^dt =2cdotfrac<(t+2)^>|_^=frac47cdot 9^-0=frac47cdot 3^7approx 1250 text end
Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin Q(t)=int_^I(t)dt end По условию: begin Q=int_^(e^+2t)dt=(-e^+t^2)|_^=-e^+6^2+e^-2^2=frac-frac+32=\ =frac+32approx 32,1 text end
Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.
Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin t=0\ t=2 end right. $$ (t=0) – начало движения, (t=2) — разворот.
 | Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум. Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно. |
Общий путь: 12+12 = 24 м.
Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.
Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) — по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin A=int_^dA=int_^pirho gH(R^2-H^2)dH=pirho gint_^(HR^2-H^3)dH=\ =pirho gleft(fracR^2-fracright)|_^=pirho gleft(frac-frac-0right)=fracpi 4=rho gR^4 end Ответ: (A=fracpi 4=rho gR^4)
Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с 2 , радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с 2 (R_E=6371) км.
Ускорение свободного падения на поверхности планеты: (g_0=Gfrac)
Ускорение свободного падения при подъеме на высоту x: begin g(x)=Gfrac end Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin A=int_^mg(x)dx=mint_^Gfracdx=GmMint_^frac=\ =GmMcdotleft(-fracright)|_^=GmMcdotleft(-frac+frac1Rright)=GmMleft(frac1R-fracright)=\ =GmMfrac=GmMfrac end Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=fracfrac=mg_0frac
$$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac=frac $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac=frac=frac, frac=fracapprox 22,2 $$ На Земле работа в 22,2 раза больше.
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Другие приложения интегралов в физике
При решении физических задач изучаемый процесс разбивают на элементарные части, в пределах каждой из которых изменением соответствующих величин можно пренебречь. Теперь задача решается по формулам для постоянных величин, после чего окончательный ответ находится с помощью интегрирования.
а) Найдем работу силы при переходе материальной точки из в , если материальная точка движется по прямой линии под действием силы , направленной вдоль этой прямой, причем величина силы зависит от координаты этой точки: .
Известно, что в случае, если сила постоянна, работа равна , где — изменение координаты точки. Поэтому разобьем отрезок на элементарные части, в пределах каждой из которых считаем силу постоянной. Тогда работа силы на участке равна . Общая работа выражается интегралом
Пример 10. Найдем работу, выполняемую при переносе материальной точки, имеющей массу , из в , если притягивающая ее по закону Ньютона точка имеет массу и находится в начале координат (рис. 66).
Решение. По закону Ньютона сила тяготения равна , где — гравитационная постоянная, а — расстояние между точками. По формуле (2) получаем:
б) Найдем работу, выполненную двигателем за промежуток времени , если мощность двигателя в момент времени равна .
За элементарный промежуток времени двигатель, имеющий мощность , выполняет работу . Поэтому вся работа двигателя равна
Пример 11. Найдем работу переменного тока, изменяющегося по формуле за промежуток времени , если сопротивление цепи равно .
Решение. Как известно из физики, в случае постоянного тока мощность выражается формулой . Поэтому по формуле (3) имеем:
Заметим, что средняя мощность переменного тока равна .
в) Вычислить количество электричества, протекающее через цепь за промежуток времени , если ток изменяется по формуле .
За элементарный промежуток времени протекает количество электричества . Значит, общее количество электричества равно
В заключение рассмотрим еще один физический пример.
Пример 12. Найдем давление воды на плотину, если вода доходит до ее верхнего края и если известно, что плотина имеет вид трапеции с высотой , верхним основанием и нижним основанием .
Решение. Рассмотрим элементарный слой, находящийся на глубине и имеющий высоту (рис. 67). Легко доказать, что длина этого слоя равна . Поэтому его площадь равна
Все давление воды на плотину выражается интегралом
💥 Видео
Зачем нужен ИНТЕГРАЛ. Объяснение смыслаСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Интегральные уравнения с вырожденным ядромСкачать

Применение интегралов в физике и математикеСкачать
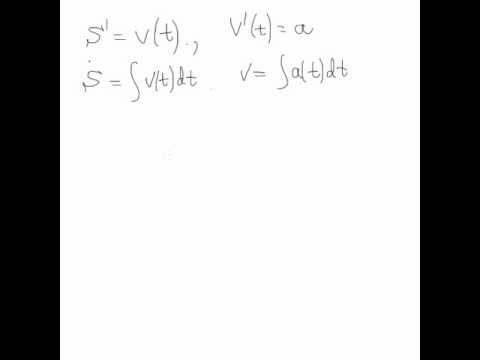
Решение физических задач с помощью дифференциальных уравненийСкачать

Интегральные уравнения ВольтерраСкачать

Урок 323. Применение производной в задачах физики - 1Скачать

Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

Билеты №32, 33 "Уравнения Максвелла"Скачать

Интегрирование в физических задачах.Скачать

Курс по ИДУ: Численное решение интегральных уравнений | Занятие 14Скачать

ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма РиманаСкачать

✓ Формула Ньютона-Лейбница. Что такое первообразная и интеграл | Осторожно, спойлер! | Борис ТрушинСкачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать






