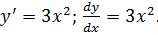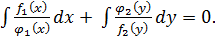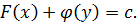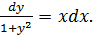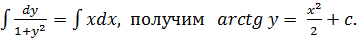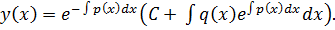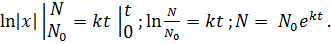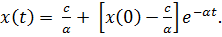Применение дифференциальных уравнений к решению задач (6 видео)

ГЛАВА 3. Применение дифференциальных уравнений первого порядка для решения прикладных задач физики, биологии, медицины

Задача 1. Скорость размножения некоторых бактерий пропорциональна количеству бактерий, имеющихся в наличии в рассматриваемый момент времени t. Количество бактерий утроилось в течение 5 часов. Найти зависимость числа бактерий от времени.

Решение. Обозначим количество бактерий в момент времени t через x, тогда — скорость размножения бактерий.

По условию задачи — уравнение с разделяющимися переменными.

Потенцируем последнее выражение и получаем общее решение нашего дифференциального уравнения.

Найдем частное решение, соответствующее начальным условиям

При t=0, x=x₀ -частное решение дифференциального уравнения.

Чтобы найти искомую зависимость, определим коэффициент пропорциональности k. По условию задачи известно, что через 5 часов .

Прологарифмируем последнее выражение

Окончательно получаем

Задача 2. При прохождении света через вещество происходит ослабление интенсивности светового потока, вследствие превращения световой энергии в другие виды энергии, т.е. происходит поглощение света веществом. Найти закон поглощения, если известно, что ослабление интенсивности пропорционально толщине слоя и интенсивности падающего излучения.

Решение. Исходя из условия задачи, можно сразу написать дифференциальное уравнение

где dI -ослабление интенсивности при прохождении слоя толщиной dx.

k -коэффициент пропорциональности.

Знак минус показывает, что интенсивность падает по мере прохождения слоя.

Проинтегрируем наше уравнение, предварительно разделив переменные

Исходя из того, что падающий на поверхность вещества свет имел интенсивность I=I₀ _, при x=0, найдем частное решение

Итак, мы получили закон поглощения света веществом ( закон Бугера), где
k -натуральный показатель поглощения.

Задача 3. Известно, что механические свойства биологических объектов изучаются с помощью вязкоупругих моделей (поршень — пружина). Одной из найболее распространенных является модель Кельвина — Фойхта, состоящая из параллельно соединенных пружины и поршня (см. рис.1).

Рис. 4. Модель Кельвина — Фойхта

Найти зависимость деформации от времени , если к модели приложена постоянная нагрузка.

Решение. Согласно условию задачи , и учитывая также, что при малых деформациях выполняется закон Гука, т.е. , а механическое напряжение, возникающее в вязкой среде пропорционально скорости деформации, т.е. , мы можем написать дифференциальное уравнение.

, или

Проинтегрируем полученное дифференциальное уравнение от начального момента времени и нулевой деформации до текущих значений t и , мы будем иметь сразу частное решение.

Потенцируя последнее выражение, получаем

Находим отсюда

Как видно из полученной формулы, в рамках модели Кельвина — Фойхта деформация при постоянной нагрузке возрастает с течением времени. Это соответствует реальным материалам. Такое свойство материала названо текучестью.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Применение дифференциальных уравнений первого порядка для решения задач

Раздел 1. Математический анализ

Тема 1.4. Дифференциальные уравнения и их применения в медицине

1. Основные понятия и определения дифференциального уравнения.

2. Методы решения некоторых дифференциальных уравнений.

3. Применение дифференциальных уравнений первого порядка для решения задач.

Основные понятия и определения дифференциального уравнения

Опр. Равенство, связывающее независимую переменную х, неизвестную функцию у = f(x), а так же её производные y’,y”,….. y n , называется обыкновенным дифференциальным уравнением.

F(x,y.y’,y”………) = 0, где F – известная функция, заданная в некоторой фиксированной области; х – независимая переменная; у – зависимая переменная; y’,y”,….. y n – её производные.

Опр. Решением дифференциального уравнения называется функция у = f(x), которая будучи представлена в уравнении F(x,y.y’,y”………) = 0, обращает его в тождество. График этой функции называется интегральной кривой.

Пример 1.1. Дифференциальное уравнение

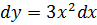
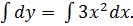
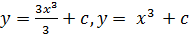
Представим в виде: ; возьмём интеграл от левой и правой части уравнения: Получим – общее решение дифференциального уравнения, которое включает произвольную постоянную с.

Методы решения некоторых дифференциальных уравнений

Выбор метода решения дифференциального уравнения зависит от его вида.

Дифференциальные уравнения первого порядка с разделяющимися переменными.

Уравнения вида называется уравнением с разделяющимися переменными, если функция разлагаются на множители, зависящие каждый только от одной переменной:

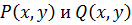
После резделения переменных, когда каждый член будет зависеть только от одной переменной, общий интеграл уравнения находится почленным интегрированием:

Решением этого уравнения будет:

Пример 2.1. Найти решение уравнения: .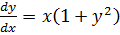

Разделим уравнение на множители, зависящие только от одной переменной:

Проинтегрируем левую и правую части:

Общее решение:

Линейные дифференциальные уравнения первого порядка.

Опр. Уравнения вида: , где – непрерывные функции, называются линейными дифференциальными уравнениями первого порядка.

При уравнение – называется линейным однородным уравнением. Общее решение:

При уравнение – называется линейным неоднородным уравнением. Общее решение: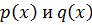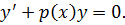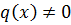

Применение дифференциальных уравнений первого порядка для решения задач

Этапы решения задач с помощью дифференциальных уравнений:

1. Оформить условия, в которых протекают изучаемые процессы;

2. Выбрать зависимые и независимые переменные;

3. Определить функциональные зависимости между ними

4. Решение уравнения;

5. Анализ полученных решений.

В уравнениях, описывающих медико-биологические процессы, в качестве независимой переменной чаще всего используется временная компонента.

Размножение бактерий

Если бактерии обитают в благоприятной среде, то скорость размножения бактерий пропорциональна размеру популяции. Такое предположение описывается дифференциальным уравнением: 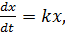где х – количество бактерий; k – коэффициент пропорциональности. Тогда, разделяя переменные и интегрируя левую и правую части уравнения получим: где N₀ – начальное количество бактерий; N — количество бактерий в момент времени t.

Вычислим определённые интегралы:

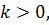
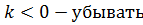
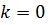
Получим экспоненциальную кривую, которая зависит от времени и k. Если то количество бактерий будет возрастать по экспоненциальному закону, при , а при — оставаться на постоянном уровне.

N₀

k 0

Для определения значения k необходимо иметь дополнительные сведения об изменении численности бактерий за определённый промежуток времени.

Внутривенное введение глюкозы

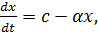
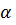
При внутривенном введении с помощью капельницы скорость поступления глюкозы в кровь постоянна и равна с. В крови глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Тогда дифференциальное уравнение, описывающее этот процесс, имеет вид: где х – количество глюкозы в крови в текущий момент времени; с – скорость поступления глюкозы в кровь; — положительная постоянная. Запишем это уравнение в виде:

Это неоднородное линейное дифференциальное уравнение первого порядка, и его общее решение находиться по формуле:

где k- постоянная интегрирования. Чтобы найти постоянную k, необходимо знать начальное значение глюкозы в крови х (0).

Тогда .

Частное решение уравнения 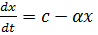имеет вид:

При увеличении времени уровень глюкозы в крови приближается к .

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Применение дифференциальных уравнений к решению задач

Дифференциальные уравнения. Тезисы. Примеры применений.

Тип публикации: Тезисы

Язык: Русский

Enter the password to open this PDF file:

Григоренко М.Н., Уральский государственный экономический университет, г. Екатеринбург Дифференциальные уравнения и их применение Изучая разделы математики можно рассматривать решение задач с использованием математического аппарата, например таких как, методы расчета рисковых оптимального временного ситуаций, использования ряда [2]. Более выбор оптимального ресурсов, анализ подробно портфеля, и задачи прогнозирование рассмотрим применение дифференциальных уравнений. Дифференциальные уравнения — раздел математики, изучающий теорию и способы решения уравнений, содержащих искомую функцию и ее производные различных дифференциальные) или порядков одного нескольких аргумента аргументов (обыкновенные (дифференциальные уравнения в частных производных) [1]. В самом уравнении участвует не только неизвестная функция, но и различные ее производные. Дифференциальным уравнением описывается связь между неизвестной функцией и ее производными. Такие связи отыскиваются в различных областях знаний: в механике, физике, химии, биологии, экономике и др. Дифференциальные уравнения применяются для математического описания природных явлений. Так, например, в биологии дифференциальные уравнения применяются для описания популяции; в физике многие законы можно описать с помощью дифференциальных уравнений. Широкое применение находят дифференциальные уравнения и в моделях экономической динамики. В данных моделях отражается не только зависимость переменных от времени, но и их взаимосвязь во времени. Рассмотрим одну из задач макроэкономической динамики [1]. Например, пусть y(f) — объем продукции некоторой отрасли, реализованной к моменту времени t. Будем полагать, что вся производимая отраслью продукция реализуется по некоторой фиксированной цене р, т.е. выполнено условие ненасыщаемости рынка. Тогда доход к моменту времени t составит Y (t )  py(t ) Обозначим через I(t) величину инвестиций, направляемых на расширение производства. В модели естественного роста полагают, что скорость выпуска продукции (акселерация) пропорциональная величине инвестиций, т.е. y’ (t )  lI (t ) , где 1/l – норма акселерации. (Здесь мы пренебрегаем временем между окончанием производства продукции и ее реализацией, то есть считаем, что инвестиционный лаг равен нулю). Полагая, что величина инвестиций I(t) составляет фиксированную часть дохода, получим I (t )  mY (t )  mpy(t ) , где коэффициент пропорциональности m (так называемая норма инвестиций) — постоянная величина ( 0  m  1 ). Подставляя последнее выражение для I(t) в y’ (t )  lI (t ) приходим к уравнению y’  ky , где k  mpl . Полученное дифференциальное уравнение — с разделяющимися переменными. Решая его, приходим к функции y(t )  y0 e k ( t t0 ) , где y0  y(t 0 ) . Заметим, что уравнение y’  ky описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и др. Модель роста в условиях роста конкурентного рынка имеет вид y’ mlp( y) y . Научный руководитель Кныш А.А., старший преподаватель Список литературы: 1. Высшая математика для экономического бакалавриата: учебник и практикум / Н. Ш. Кремер, Б. А. Путко, И. М. Три-шин, М. Н. Фридман; под ред. Н. Ш. Кремера. – М.: Издательство Юрайт; ИД Юрайт, 2012. — 909 с. 2. Кныш А.А. Примеры реализации межпредметных связей на занятиях математики в экономическом вузе // Новая наука: от идеи к результату. — Стерлитамак: АМИ, 2017. — №2 (2) – С. 55 – 57.