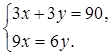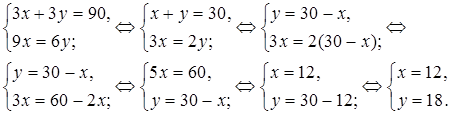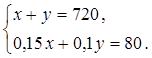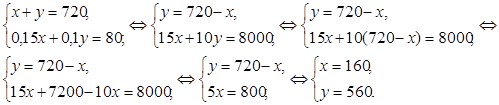Прикладная задача на составление уравнения задание (2 видео)

Прикладные задачи по тригонометрии

Разделы: Математика

Цель данной статьи — обоснование роли прикладных задач курса тригонометрии на уроках математики.

Одним из направлений модернизации современного математического образования является усиление прикладной направленности школьного курса математики, то есть осуществление связи его содержания с практикой.

В педагогических исследованиях прикладная направленность математики понимается как содержательная и методическая связь школьного курса с практикой, что предполагает у учащихся наличие умений, необходимых для решения средствами математики практических задач. А так как в основе их решения лежит математическое моделирование, то для реализации прикладной направленности необходимо организовать обучение школьников элементам моделирования, которыми с дидактической точки зрения являются учебные действия, выполняемые в процессе решения задач.

Кроме того, для реализации прикладной направленности математики существенное значение имеет использование в преподавании различных активных форм и методов организации учебного процесса, которые построены на коммуникативном взаимодействии и самостоятельном добывании и применении знаний самими учащимися: мозговая атака и мозговой штурм, метод проектов, тренинг, исследовательский метод, деловые игры и др.

В данной статье рассмотрен фрагмент одного из уроков математики, проведенного в форме деловой игры «Метод проектов» [1]. В статье опущены подробные описания этапов организации урока (они известны учителям, использующим интерактивные методы обучения), а рассмотрены лишь содержательные аспекты урока.

Содержание

Микрогруппа 1
Микрогруппа 2
Микрогруппа 3
Решение уравнений. Решение задач прикладного содержания. методическая разработка по алгебре (11 класс) на тему
Скачать:
Предварительный просмотр:
Задачи на составление уравнений
💥 Видео

Микрогруппа 1

Задача 1. При планировании графика полета, пилот должен рассчитать скорость, v км/ч, на плоскости, принимая во внимание скорость и направление ветра. Скорость в км/ч можно выразить в виде . Без использования калькулятора, найти значение v, если .

Задача 2. Найти высоту горы. (рис.1)

Задача 3. Электрическая цепь. В колебательном контуре, заряд, q Кулонов, задан формулой , где t — время в секундах после включения схемы.

Найдите первоначальный заряд.
Найдите значения А и В, если дано, что , где
Выведите значение заряда с течением времени.

Микрогруппа 2

Задача 1. Популяция насекомых. Эколог, изучающий вид жука, оценивает популяцию колонии в течение восьми недель. Если t — это количество недель после первоначальной оценки, то численность насекомых в тысячах может быть смоделирована формулой , где .

Какова была первоначальная численность вида?
Каковы были самое маленькое и самое большое число популяции?
В течение какого интервала(ов) численность превышала 6000?

Задача 2. С подножия здания я должен смотреть 22 o вверх, чтобы посмотреть на вершину дерева. С вершины здания, на высоте 150 метров над уровнем земли, я должен смотреть вниз под углом 50 o ниже горизонтали, чтобы увидеть вершину дерева. (рис. 2)

Насколько высоко дерево?
Как далеко от здания растёт это дерево?

Задача 3. Равновесие. Диаграмма показывает шар P, присоединенный к двум струнам, которые наклонены под углами А и Q к горизонтали. Напряженностью в струнах являются 10 N (то есть ньютонов) и F N. Усилие на мяче под воздействием силы тяжести составляет 20 N. (рис.3) Когда мяч находится в равновесии, то можно показать, что

Используйте тождество , чтобы выразить F через A.
Показать, что
Найти точные значения F и учитывая, что A = 30 o .

Микрогруппа 3

Задача 1. Приливы. Высота, в метрах, приливов регистрируется на определенном пляже со временем t часов. Обнаружено, что высота y m, задается уравнением .

Нарисуйте график y для .
Найти высоту прилива через 4 часа с начала исследования.

Задача 2. Башня связи. Как показано на рисунке, башня связи построена наверху здания. Найдите высоту башни. (рис.4)

Задача 3. Артериальное давление. Джерри измерил своё артериальное давление P (в мм ртути) со временем и обнаружил, что функция , где t > 10, примерно соответствует его артериальному давлению в момент времени t (в секундах). Найдите наименьшее значение t больше 10, для которого P = 100 .

Наблюдения и анализ уроков показывают, что уроки, построенные в форме группового общения имеют большое значение для развития учащихся. Кроме того, решение прикладных задач повышает мотивацию обучения.

Литература

1. Полат Е.С., Бухаркина М.Ю., Моисеева М.В., Петров А.Е. Новые педагогические технологии в системе образования. — М.: Академия, 2000.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Решение уравнений. Решение задач прикладного содержания.
методическая разработка по алгебре (11 класс) на тему

Урок итогового повторения «Решение уравнений. Решение садач практического содержания». Данный урок может быть использован при подготовки к ЕГЭ в 11 классе.

Видео:Математика 6 класс. Решение задач на составление уравненийСкачать

Скачать:

Вложение	Размер
tema_uroka.docx	27.23 КБ
ustnyy_schet.pptx	153.56 КБ

Видео:Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Предварительный просмотр:

Урок итогового повторения: Решение уравнений. Решение задач прикладного содержания. 11 класс

Автор: Шемарова Татьяна Анатольевна, учитель математики МОУ «Средняя школа №16», г.Кимры, Тверской области.

Предмет: алгебра и начала анализа.

Цель урока : 1) умение анализировать условие задачи, умение логически мыслить, умение выделять основные этапы решения, умение конкретизировать и обобщать, умение анализировать полученный результат, умение делать выводы.

Образовательные — повторить алгоритм решения логарифмических, показательных, иррациональны, дробно-иррациональных уравнений, применение уравнений при решении задач прикладного содержания, оценка знаний полученных учащимися.

Развивающие — развитие логического и пространственного мышления учащихся; память; анализ.

Воспитательные — эстетическое воспитание; воспитание ответственности за конечный результат, самостоятельности.

I. Организационный момент. Постановка цели урока. Перед нами стоит задача: повторить виды, методы и особенности решения логарифмических, показательных и иррациональных уравнений и применить их на практике. Только личный труд каждого в изучении математики может принести результаты.

Наши знания должны работать и дать положительный результат на экзамене. Сегодня Маша, Даша Зина и Наташа проверят свои знания и умения решать уравнения, Вам предлагается решить по 4 уравнения. В соответствии с этой оценкой мы постараемся устранить имеющиеся пробелы.

А мы с вами повторим решение уравнений. Внимание на доску, решаем уравнения.

II. Устная работа:

1. Найдите корни уравнения:

Вопросы к учащимся при решении устных заданий:

Повторить алгоритм решения логарифмических, показательных, иррациональных уравнений.
Что надо учитывать при решении логарифмических уравнений и иррациональных уравнений.
Решение тригонометрических уравнений.

Четверо учащихся в это время решают устно на местах индивидуальные задания.

III. Работа с текстом заданий.

В заданиях ЕГЭ встречаются задания (конкретно – задания В5, В12, В13, С1, С5), где возникает необходимость в знании и умении решать уравнения.

Сегодня мы вместе будем выполнять задания типа В12 и С1. У Вас на партах лежат памятки по выполнению задания В12, сейчас выполняем вместе используя данную памятку будем выполнять задания на доске.

В ходе распада радиоактивного изотопа его масса уменьшается по закону

m(t) = , где (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа =40 мг. Период его полураспада T=10 мин. Через сколько минут масса изотопа будет равна 10 мг?

Для обогрева помещения, температура в котором равна , через радиатор отопления, пропускают горячую воду температурой . Расход проходящей через трубу воды m=0,3 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры T(˚C) , причeм x=α (м), где c= 4200 — теплоeмкость воды,γ =21 — коэффициент теплообмена, а α=0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м?
В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону H(t)=a , где =6м — начальный уровень воды, м/мин2, и b= — м /мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

Сейчас мы с частью учащихся будем решать задания С1, а на парте у учащихся лежат задания это перевернутые листочки, вы выполняете в тетрадях для подготовки к ЕГЭ.

IV. Самостоятельная работа

Далее работаем параллельно часть учеников выполняет часть 2 С1, а тем кто не решает вторую часть выполняет самостоятельную работу.

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h=5 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q=100-10p . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p)=q•p . Определите наибольшую цену p , при которой месячная выручка r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой η= , где — температура нагревателя (в градусах Кельвина), — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя КПД этого двигателя будет не меньше 25%, если температура холодильника К? Ответ выразите в градусах Кельвина.

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h=5 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 1,4 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q=130-10p . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p)=q•p . Определите наибольшую цену p , при которой месячная выручка r(p) составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой η= , где — температура нагревателя (в градусах Кельвина), — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя КПД этого двигателя будет не меньше 15%, если температура холодильника К? Ответ выразите в градусах Кельвина.

б) Найдите все корни уравнения принадлежащие, промежутку

б) Найдите все корни уравнения принадлежащие, отрезку промежутку

Д/З: а) Решите уравнение =4

б) Найдите все корни уравнения принадлежащие, промежутку

Домашнее задание: Выполнить 5 заданий В12 (различные) из Открытого банка заданий ЕГЭ по математике.

1) Алгебра и начала анализа для 10 класса, авторов: Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова и М.И. Шабунин, под редакцией А.Б. Жижченко. – М. Просвещение, 2009.

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Задачи на составление уравнений

Задачи на составление уравнений

Бригада рабочих должна была выполнить заказ за 5 дней. Ежедневно превышая норму на 18 деталей, она за 3,5 дня работы не только выполнила задание, но и изготовила 27 деталей сверх плана. Сколько деталей изготовила бригада?

В упаковке находится 2 кг смеси сухофруктов. Чернослива в этой смеси в 1,6 раза больше, чем яблок, а изюма на 0,2 кг больше, чем яблок. Сколько яблок, чернослива и изюма в упаковке в отдельности?

Каждый из двух пешеходов прошел по 6 км. Скорость первого пешехода на 3 км/ч больше скорости второго, а поэтому время, которое был в пути первый пешеход, отличается от времени второго пешехода на 1 час. Сколько времени был в пути первый пешеход?

Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от пункта А. Найдите скорость каждого, если известно, что пешеход, вышедший из А, шел со скоростью на 1км/ч большей, чем второй пешеход, и сделал в пути получасовую остановку.

Катер, собственная скорость которого 8 км/ч, прошел по реке расстояние, равное 15 км/ч, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.

Зарплата лаборанта составляла 100 рублей в месяц, после двух последовательных повышений на одно и то же число процентов она стала составлять 121 р. На сколько процентов каждый раз повышалась зарплата лаборанта?

За 3 м одной ткани и 3 м другой заплатили 90 рублей. Сколько стоит 1 м каждой ткани, если 9 м первой ткани стоят столько же, сколько 6 м второй ткани?

В двух корпусах пансионата было 720 мест для отдыхающих. После реконструкции в первом корпусе число мест увеличилось на 15 %, а во втором – на 10 %. Сколько мест для отдыхающих стало в каждом корпусе, если общее число мест в обоих корпусах увеличилось на 80?

Обозначим через х количество деталей, которое бригада планировала изготавливать за один день. Тогда, выполнив заказ за 5 дней, она по плану должна была изготовить 5х деталей, но превышая норму, бригада изготовляла в день (х + 18) деталей, значит, за 3,5 дня она сделала (х + 18) · 3,5 деталей. По условию задачи бригада за 3,5 дня не только выполнила задание, но и изготовила 27 деталей сверх плана. С учетом этого составляем уравнение: (х + 18) · 3,5 = 5х + 27.

Решаем полученное уравнение (х + 18) · 3,5 = 5х + 27.

5х – 3,5х = 63 – 27; 1,5х = 36; х = 24. Значит, бригада планировала изготовлять в день по 24 детали, а делала 24 + 18 = 42 детали; тогда за 3,5 дня она сделала 42 · 3,5 = 147 деталей.

О т в е т: 147 деталей.

Пусть в упаковке х кг яблок, тогда чернослива в ней 1,6х кг, а изюма – (х + 0,2) кг. Вся смесь имеет массу 2 кг.

Уравнение: х + 1,6х + х + 0,2 = 2.

Решение уравнения: 3,6х = 2 – 0,2,

В упаковке 0,5 кг яблок, 0,7 кг изюма и 0,8 кг чернослива.

О т в е т: 0,5 кг; 0,7 кг; 0,8 кг.

Пусть первый пешеход был в пути х часов, тогда 6 км он прошел за км/ч. Так как скорость первого пешехода была больше скорости второго, то второй пешеход на такое же расстояние времени затратил, по условию задачи, на 1 час больше. Значит он в пути был (х + 1) часов и его скорость была ровна км/ч.

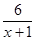
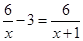
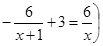
По условию задачи скорость первого пешехода была больше скорости второго пешехода на 3 км/ч. С учетом этого составляем уравнение: . (Уравнение также можно записать в виде , или .

Решаем полученное уравнение:

; ; ; ;

;

+ х – 2 = 0;

;

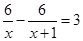
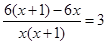
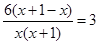
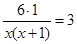
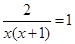
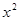
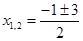
При х1 = 1 х(х+1) ? 0; при х2 = –2 х(х + 1) ? 0. значит х1 = 1 и х2 = –2 – корни уравнения, но значение х2 = –2 условию задачи не удовлетворяет, так как время движения пешехода не может быть выражено отрицательным числом. Следовательно, х = 1.

О т в е т: первый пешеход был в пути 1 час.

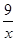
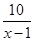
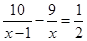
Обозначим скорость пешехода, вышедшего из пункта А, – х км/ч, тогда скорость второго пешехода – (х – 1) км/ч. Первый пешеход был в пути ч, а второй – ч. По условию задачи пешеходы вышли одновременно и встретились, но второй пешеход делал остановку на ч, следовательно, можно составить уравнение: .

Решение уравнения: Решение уравнения: 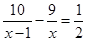, НОЗ: 2х(х – 1).

D = 9 + 4 · 18 = 91,

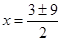
При х = 6 2х(х – 1) ? 0, при х = –3 2х(х – 1) ? 0, значит, х = 6 и х = –3 – корни составленного уравнения, но х = –3 не удовлетворяет условию задачи, остается х = 6. Скорость пешехода, вышедшего из пункта А – 6 км/ч, скорость второго 6 – 1 = 5 км/ч.

О т в е т: 6 км/ч, 5 км/ч.

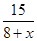
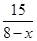
Пусть хкм/ч – скорость течения реки, тогда скорость катера по течению (8 + х) км/ч, а против течения – (8 – х) км/ч, и время движения по течению ч, а против течения ч. По условию задачи время, затраченное на весь путь, равно 4 ч.

Уравнение: .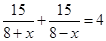

Решение уравнения: 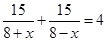;НОЗ: (8 + х)(8 – х),

При х = 2 (8 + х)(8 – х) ≠ 0, при х = –2 (8 + х)(8 – х) ≠ 0, значит х = 2 и х = –2 – корни уравнения, но х = –2 условию задачи не удовлетворяет, следовательно, х = 2, т. е. скорость течения реки 2 км/ч.

О т в е т: 2 км/ч.

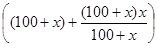
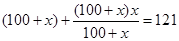
Пусть зарплата лаборанта повышалась каждый раз на х %, тогда первый раз она повысилась на 100 : 100 · х = х руб. и стала составлять (100 + х) рублей. Во второй раз она повысилась на (100 + х) : 100 · х рублей и стала составлять после этого рублей, достигнув, по условию задачи, размера 121 рубль в месяц. С учетом этого составляем уравнение: .

Решаем полученное уравнение:

;

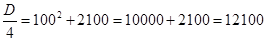
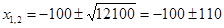
Значит, х = –210 и х = 10 – корни уравнения, но значение х = –210 условию задачи не удовлетворяет, так как является отрицательным числом. Следовательно, зарплата лаборанта дважды повышалась на 10 %.

Пусть один метр первой ткани стоит х рублей, а один метр второй ткани стоит у рублей. Тогда 3 м первой ткани стоят 3х рублей, а 3 м второй ткани стоят 3у рублей. Так как по условию задачи за 3 м одной ткани и 3 м второй заплатили 90 рублей, составляем уравнение: 3х + 3у = 90.

Поскольку 9 м первой ткани стоят 9х рублей, а 6 м второй ткани стоят 6у рублей, а по условию задачи 9 м первой ткани стоят столько же, сколько 6 м второй ткани, составляем второе уравнение: 9х = 6у.

Так как х и ув обоих уравнениях обозначают одни и те же величины, можно составить систему уравнений:

Решаем систему уравнений.

Итак, решение системы: (12; 18). Значит, 1 м первой ткани стоит 12 рублей, а 1 м второй – 18 рублей.

О т в е т: 12 р., 18 р.

Пусть в первом корпусе было х мест, а во втором у мест. Так как по условию задачи в обоих корпусах вместе было 720 мест, то можно составить уравнение: х + у = 720.

Поскольку число мест в первом корпусе увеличилось на 15 %, то есть на 0,15х мест, а во втором – на 10 %, то есть на 0,1у мест, причем общее число мест в обоих корпусах увеличилось на 80, то можно составить второе уравнение: 0,15х + 0,1у = 80.

Итак, имеем систему уравнений:

Решаем полученную систему уравнений:

Значит, в первом корпусе первоначально было 160 мест, затем стало: 160 · 1,15 = 184; во втором корпусе первоначально было 560 мест, затем стало: 560 · 1,1 = 616 мест.

О т в е т: 184 места и 616 мест.

ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

По шоссе движутся две автомашины с одной и той же скоростью. Если первая машин увеличит свою скорость на 10 км/ч, а вторая – уменьшит на 10 км/ч, то первая автомашина за 5 часов пройдет столько же, сколько вторая за 7 часов. С какой скоростью движутся автомашины?

Два токаря должны изготовить по 40 деталей. Сколько деталей в час изготавливал первый токарь, если второй, изготавливая на 3 детали в час меньше, затратил на всю работу на 3 часа больше?

Группа школьников купила мороженое, уплатив за покупку 1 р. 45 к. монетами достоинством в 10 к. и 15 к. Сколько монет по 10 к. и сколько монет по 15 к. отдали школьники за покупку, если всего было отдано 11 монет?

О т в е т: 60 км/ч.

О т в е т: 8 деталей в час.

О т в е т: 4 монеты по 10 к. и 7 монет по 15 к.