Приборы магнитоэлектрической системы уравнение шкалы (3 видео)

Магнитоэлектрические приборы

Магнитоэлектрические приборы применяются в качестве амперметров, вольтметров и гальванометров для измерений в цепях постоянного тока, а в сочетании с преобразователями переменного тока в постоянный – и для измерений в цепях переменного тока.

Узел для создания вращающего момента состоит из сильного постоянного магнита и легкой подвижной катушки, по которой протекает измеряемый ток (Рис.5, а).

Обмотка подвижной катушки состоит из витков тонкого провода, поэтому магнитоэлектрический прибор можно применять непосредственно только в качестве микро- или миллиамперметра и милливольтметра.

Катушка в форме прямоугольной рамки помещена в кольцевом зазоре между полюсными наконечниками магнита и цилиндрическим сердечником, т.е. в радиальном магнитном поле. Принцип действия магнитоэлектрических приборов заключается во взаимодействии поля постоянного магнита с проводником (катушкой), по которому протекает измеряемый ток. При этом возникает пара сил F (Рис.5, б), создающая вращающий момент. Энергия магнитоэлектрической системы является суммой энергии поля магнита W_п.м_. , энергии катушки с током и энергии взаимодействия поля магнита и катушки с током YI, где Y — потокосцепление, численно равное произведению числа силовых магнитных линий, пересекаемых обеими сторонами катушки при ее повороте на угол а, на число витков n ее обмотки:

(5)

Здесь В – магнитная индукция в зазоре, Тл; s – площадь обеих сторон катушки, м 2 .

Таким образом, вся энергия, сосредоточенная в узле, вызывающем вращающий момент, равна

(6)

На основании формулы (1), дифференцируя выражение (6) по перемещению, получим уравнение вращающего момента

(7)

На основании формулы (2) отклонение подвижной части прибора подчинено следующей зависимости:

(8)

где S_i = Bns/W – чувствительность прибора по току.

Формула (8) является уравнением шкалы прибора магнитоэлектрической системы. Из этого уравнения следует, что отклонение указателя пропорционально измеряемому току, шкала равномерна (линейна), при включении следует соблюдать полярность, так как прибор чувствителен к постоянному току. При включении прибора в цепь по которому протекает пульсирующий или импульсный ток, отклонение указателя будет пропорционально постоянной составляющей (среднему значению) этих токов; в цепи с током синусоидальной формы вследствии инерционности подвижной части показания будут равны нулю и лишь при частоте переменного тока ниже 10 Гц подвижная часть с указателем будет совершать колебательные движения.

Время установления показаний сокращается с помощью электромагнитного успокоения, возникающего за счет индуцированного тока в катушке, возбуждаемого при пересечении ею магнитного поля: I = e/R_S , где е – индуцированная ЭДС, а R_S – сумма сопротивлений подвижной катушки и внешней цепи, на которую она замкнута;

Находим момент электромагнитного успокоения

Коэффициент успокоения в соответствии с формулой (4)

(9)

Для увеличения коэффициента успокоения нужно уменьшиь общее сопротивление, что не всегда возможно. Выход состоит в том, что катушка наматывается на алюминиевом каркасе, в котором индуцируется ЭДС; тогда формула (9) примет вид:

где R_k – электрическое сопротивление каркаса.

Если катушку утяжелять нежелательно, то она выполняется бескаркасной (витки склеиваются), а для получения индуцированной ЭДС наматывают дополнительный короткозамкнутый виток.

Имеются конструкции магнитоэлектрических приборов с неподвижной катушкой и подвижным магнитом на одной оси с указателем (рис. 5,в ).

К достоинствам магнитоэлектрических приборов относятся: высокая чувствительность (до 3*10 -11 А); высокая точность (до класса 0,05); малое потребление мощности от измеряемой цепи (10 -5 – 10 -6 Вт); влияющая величина –температура окружающей среды.

Недостатки: сложность изготовления и ремонта; недопустимость даже кратковременных перегрузок (деформируются или перегорают токоподводящие пружинки, нити растяжек и подвесов).

Амперметры. Для измерения токов параллельно зажимам прибора присоединяется электрический шунт представляющий собой прямоугольную манганиновую пластину. Для измерения токов выше 50 А применяют наружние шунты. Переносные приборы снабжаются внутренними многопредельными шунтами или наружными наборами шунтов на несколько номинальных токов. Выбор шунта для данного прибора зависит от заданного расширения пределов измерения m= I/I_Aи внутреннего сопротивления прибора (сопротивления его катушки) R_A. Для электрической цепи, приведенной на рис.6, а, справедливы следующие равенства: I_aR_a=I_шR_ш; I=mI_a; I_ш=I-I_a. Отсюда находим сопротивление шунта: R_ш=R_аI_a/I_ш=R_aI_a/(mI_a-I_a)=R_a/(m-1). Через катушку прибора будет протекать (1/m)-я часть измеряемого тока, а через шунт – в (m-1) раз больше.

Погрешность шунтированного амперметра возрастает вследствие неточности изготовления шунтов (от 0,005 до 0,5%) и различных температурных коэффициентов сопротивления катушки и шунта.

Вольтметры. При параллельном подключении магнитоэлектрического прибора к участку электрической цепи можно измерить напряжение. В этом случае уравнение (8) примет вид:

, (10)

где S_u – чувствительность вольтметра по напряжению; R_v – сопротивление проводов катушки.

Сопротивление обмотки катушки мало и для измерения больших напряжений последовательно ей включают добавочные резисторы с сопротивлением R_д. Пусть задано расширить предел измерений в m=U/U_v раз. Для электрической цепи представленной на рис. 6, б, можно написать: U_Rд/R_д=U_v/R_v, откуда R_д=R_vU_Rд/U_v=R_v(m-1). Значит на катушке прибора падение напряжения составит (1/m)-ю часть измеряемого напряжения, а на добавочном резисторе в (m-1) раз больше. В формуле (10) вместо R_v нужно подставить R_v+R_д.

Гальванометры. Особо чувствительные магнитоэлектрические приборы для измерения токов, напряжений и количества электричества. Гальванометры часто используют в качестве нулевых индикаторов, показывающих отсутствие тока в цепи. Для этого выпускаются гальванометры с двухсторонней шкалой, т.е. с нулевой отметкой посередине.

Гальванометры разделяются на переносные и стационарные. Подвижная катушка у переносных гальванометров крепится на растяжках; внутреннее отсчетное устройство снабжено оптическим указателем. Стационарные (зеркальные) гальванометры выполняют с подвесом рамки (катушки) и внешней шкалой, на которую падает луч света, отраженный от зеркальца (Рис.2,в). Легкая катушка и малый удельный противодействующий момент создает условия для возникновения механических затухающих колебаний подвижной части гальванометра (Рис.7, кривая 1). Для убыстрения затухания колебаний применяют электромагнитное успокоение. Коэффициент успокоения (9)

где R_г – сопротивление проводов рамки гальванометра; R_н – сопротивление наружного резистора (цепи), на который замкнута рамка.

Зная, что P=f(R_г+R_н); изменяя наружное сопротивление, можно изменять коэффициент успокоения и интервал времени успокоения. Положим, что при некотором P=P_кр наступает критический режим, при котором в течении минимального интервала времени t_у наступает успокоение. Введем понятие степени успокоения b :

где R_н.кр – некоторое значение наружного сопротивления, при котором возникает критический режим.

В критическом режиме b_кр = 1 и процесс установления характеризуется кривой 3 на рис.7. Если b_кр > 1, режим апериодический (кривая 2), если b_кр

Видео:КАК РАБОТАЮТ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ [РадиолюбительTV 50]Скачать

Магнитоэлектрические приборы

Устройство. Магнитоэлектрические приборы (МЭП) состоят из ИЦ, ИМ и ОУ

(см. рис.2.1) Конструктивно измерительный механизм может быть выполнен либо с подвижным магнитом, либо с подвижной катушкой. На рис. 2.2 показана конструкция прибора с подвижной катушкой.

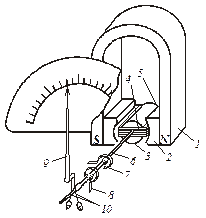
Рис.2.2. Устройство магнитоэлектрического прибора.

Постоянный магнит 1, магнитопровод с полюсными наконечниками 2 и неподвижный сердечник 3 составляют магнитную систему механизма. В зазоре между полюсными наконечниками и сердечником создается сильное равномерное радиальное магнитное поле, в котором находится подвижная прямоугольная катушка 4, намотанная медным или алюминиевым проводом на алюминиевом каркасе (применяют и бескаркасные рамки). Катушка (рамка) может поворачиваться в зазоре на полуосях 5 и 3. Спиральные пружины 7 и 8 создают противодействующий момент и используются для подачи измеряемого тока от выходных зажимов прибора в рамку (механические и электрические соединения на рисунке не показаны) Рамка жестко соединена со стрелкой 9. Для балансировки подвижной части имеются передвижные грузики 10.

Принцип действия.Проходя по проводникам обмотки рамки, ток I взаимодействует с магнитным потоком постоянного магнита, что вызывает появление механических сил F, создающих вращающий момент Мвр для рамки. Из теоретических основ электротехники известно выражение для механической работы, совершаемой при перемещении проводника с током в магнитном поле:

где F— сила, действующая на проводник в направлении элементарного перемещения dα; dW_М — изменение запаса энергии магнитного поля.

Если проводник движется по окружности с радиусом r, то

где dα — элементарный угол поворота.

Здесь F_r— вращающий момент — М_ВР, т. е.

Тогда окончательно запишем:

Это уравнение является обобщенным выражением вращающего момента для всех приборов, в которых используют сила электромагнитного поля

Противодействующий момент в приборах необходим для создания однозначного соответствия измеряемой величины определенному углу отклонения подвижной части. В аналоговых электромеханических приборах противодействующий момент создается либо при помощи спиральных пружин (растяжек и подвесов), либо за счет энергии электромагнитного поля (в логометрах).

В случае, когда противодействующий момент создается спиральной пружинкой

где W – удельный противодействующий момент, зависящий от геометрических размеров и материала пружины (растяжек)

Уравнение шкалы.Выражение для вращающего момента, действующего на рамку при протекании по ней тока I, может быть получен, исходя из обобщенного выражения вращающего момента (2.1). Запас электромагнитной энергии в контуре с током I, находящемся в поле постоянного магнита, выражается формулой:

где Ψ— полное потокосцепление данного контура с магнитным полем постоянного магнита. Тогда

При повороте рамки на угол dα каждая ее сторона опишет дугу dα·b/2, пересекая при этом силовые линии магнитного поля; число пересеченных линий будет равно произведению пройденного пути dα·b/2 на длину активной стороны рамки l и на индукцию в зазоре В.

Полное изменение потокосцепления с рамкой равно произведению числа силовых линий, пересеченных обеими сторонами рамки, на число витков ее обмотки, т. е.

где ω — число витков обмотки.

Произведение·Βl равно площади рамки; обозначив еечерез S,получим:

Если положить dα =1 рад, то произведение BSω — величина постоянная для каждого данного прибора — будет равна изменению потокосцепления при повороте рамки на 1 рад. Обозначая его через Ψ₀, запишем:

Подставляя выражение (2.5) формулу (2.3), получим выражение вращающего момента для магнитоэлектрического механизма в следующем виде:

Установившееся положение подвижной катушки наступает при равенстве вращающего и противодействующего моментов? М_ВР = М_ПР, т.е. с учетом (2.2) запишем:

Отсюда находим уравнение шкалы измерительного механизма магнитоэлектрической системы

где величина S = Ψ₀ / W является чувствительностью прибора (в радианах на ампер).

Используя выражение (2.4) можно ввести в уравнение шкалы конструктивные параметры измерительного механизма:

α = Bsω Ι · 1/W, (2.9)

т.е. угол отклонения подвижной части прямо пропорционален току в рамке, поэтому магнитоэлектрические приборы имеют равномерные шкалы.

Успокоение подвижной части магнитоэлектрических приборов магнитоиндукционное, т.е. создается взаимодействием магнитных полей от вихревых токов в каркасе рамки и поля постоянного магнита.

Метрологические характеристики MЭП: классы точности – 0,05; 0,1 и т.д., равномерная шкала, высокая и стабильная чувствительность, малое собственное потребление мощности, большой диапазон измерений, большой МВР, успокоение только магнитоиндукционное.

Эксплуатационные характеристики: возможность использования только в цепях постоянного тока, малая нагрузочная способность, сложны и дороги, на показания прибора влияет температура, но не влияют внешние магнитные и электрические поля.

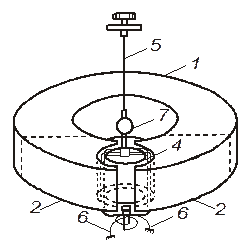Приборы магнитоэлектрической системы уравнение шкалы

Гальванометры постоянного тока. На рис. 2.5 показано устройство магнитоэлектрического гальванометра постоянного тока. Сильный постоянный магнит 1 из высококоэрцетивного сплава, полюсные наконечники 2 из магнитомягкой стали с

Рис. 2.5. Устройство магнитоэлектрического гальванометра.

цилиндрической расточкой концов, неподвижный стальной цилиндр 3 , укрепленный в расточке, служат для создания в зазоре сильного равномерного магнитного поля. В этом зазоре находится рамка 4,укрепленная на подвесе 5; ток подводится через безмоментные спирали 3. На оси рамки закреплено зеркальце 7 для оптического отсчета угла отклонения рамки от нулевого положения.

На рамку, при подаче тока I действуют моменты: вращающий М_ВР (2.6), успокоения М_У = − Р dα/dt, направленный в сторону, противоположную М_ВР. и противодействующий момент, создаваемый при закручивании подвеса М_ПР = Wα.

Величина P = Ψ₀ / (R_Г + R_ВН) называется коэффициентом успокоения и определяется конструктивными параметрами гальванометра Ψ_0, R_Г и сопротивлением внешней цепи R_ВН. Изменяя R_ВН можно изменять коэффициент успокоения.

Известно, что движение вращающегося тела определяется уравнением

где J – момент инерции тела; d 2 α/dt 2 – угловое ускорение; ΣM – сумма вращающих моментов, действующих на тело.

Для гальванометра это уравнение имеет вид:

Подставляя в уравнение (2.15) значения моментов с учетом их знака получим дифференциальное уравнение движения подвижной рамки гальванометра:

Интеграл этого дифференциального уравнения второго порядка с постоянными коэффициентами и с правой частью, как известно, состоит из двух членов: α_С –частного решения при заданных условиях и α₀ – общего решения данного уравнения без правой части, т.е.

Частное решение уравнения (2.16), рассмотренное для случая установившегося равновесия подвижной части гальванометра, когда скорость ее движения (dα/dt ) и ускорение (d 2 α/dt 2 ) будут равны нулю, через выражение (2.7) получим

Уравнение (2.16) без правой части для получения общего решения имеет вид:

Решением его будет функция

Где С₁ и С₂ постоянные интегрирования, получаемые из начальных условий; Х₁ и Х₂ – корни характеристического уравнения

JX 2 + PX + W = 0 (2.21)

Нахождение этих корней и подстановка их в выражение (2.19) и далее полученного значения α₀ в (2.17) дает искомое уравнение движения подвижной части гальванометра:

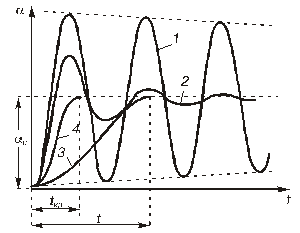График функции (2.22) для различных значений сопротивления нагрузки приведен на рис.2.3.

Рис.2.3. Режимы движения подвижной части гальванометра.

При R_ВН = ∞ колебания подвижной части гальванометра будут постепенно, хотя и медленно, затухать из-за трения подвижной рамки о воздух (кривая 1) и режим движения рамки — колебательный.

Дата добавления: 2016-03-22 ; просмотров: 2481 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Урок 179 (осн). Электроизмерительные приборыСкачать

Приборы магнитоэлектрической системы уравнение шкалы

АНАЛОГОВЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ.

АНАЛОГОВЫЕ ЭЛЕКТРОМЕХАНИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ.

Структурную схему аналогового электромеханического прибора в общем виде можно представить как:

Измерительная цепь – обеспечивает преобразование электрической величины Х в промежуточную электрическую величину Y, функционально связанную с величиной Х и пригодную для непосредственной обработки измерительным механизмом.

Измерительный механизм – основная часть прибора, предназначенная для преобразования электромагнитной энергии в механическую, необходимую для создания угла поворота a.

Отсчетное устройство – состоит из указателя, связанного с измерительным механизмом и шкалы.

Указатели – бывают стрелочные (механические) и световые.

Шкала – совокупность отметок, представляющих ряд последовательных чисел вдоль какой либо линии.

По начертанию шкалы бывают прямолинейные (горизонтальные или вертикальные), дуговые (при дуге 180°) и круговые (при дуге > 180°).

Цена деления шкалы определяются как:

где: Х – конечное значение шкала на данном пределе измерения,

N . число отметок шкалы.

Рассмотрим общий принцип действия измерительного механизма.

Обобщенная механическая схема измерительного механизма представлена на рисунке.

1 – ось, 2 – электромеханический преобразователь, приведенный к общему центру масс, 3 – стрелка, 4 – пружина, 5 – подшипниковые опоры.

Дифференциальное уравнение моментов, описывающее работу измерительного механизма, имеет вид:

где J – момент инерции подвижной части измерительного механизма,

— угол отклонения подвижной части,

— угловое ускорение.

На подвижную часть (при движении) воздействуют следующие составляющие моментов:

Вращающий момент – М- определяется скоростью изменения энергии электромагнитного поля , сосредоточенной в механизме, по углу отклонения .

Противодействующий момент — М— создается, как правило, при помощи спиральных пружин и растяжек

где: W – удельный противодействующий момент на единицу угла закручивания пружины (определяется её материалом, длиной и т.д.).

Момент успокоения – М_усп— момент сил сопротивления движению. Всегда направлен встречно вращающему моменту.

р- коэффициент успокоения (демпфирования) подвижной части.

После подстановки всех составляющих момента в основное уравнение получим:

или

В статическом режиме, т.е когда стрелка прибора находится в неподвижном состоянии при каком то угле отклонения a, можно записать:

По типу измерительного механизма приборы делятся на:

магнитоэлектрический механизм;

магнитоэлектрический механизм логометрического типа;

электромагнитный механизм;

электромагнитный механизм логометрического типа;

электромагнитный поляризованный механизм;

электродинамический механизм;

электродинамический механизм логометрического типа;

ферродинамический механизм;

ферродинамический механизм логометрического типа;

электростатический механизм:

измерительный механизм индукционного типа.

Общие технические требования ко всем электроизмерительным приборам нормируются

Условные обозначения определены в

ПРИБОРЫ МАГНИТОЭЛЕКТРИЧЕСКОГО ТИПА.

Общее устройство прибора электромагнитного типа показано на рисунке:

На рисунке а показана схема магнитоэлектрического механизма с подвижным магнитом, а на рисунке б- с неподвижным магнитом.

На рисунке приняты следующие обозначения:

стрелка; 2- катушка; 3- постоянный магнит; 4- пружина; 5- магнитный шунт; 6- полюсные наконечники.

Вывод уравнения шкалы прибора.

Уравнением шкалы называется математическая зависимость, дающая связь между измеряемой величиной и углом отклонения стрелки прибора.

Обозначим потокосцепление, связанное с катушкой как , тогда:

=I, где — энергия электромагнитного поля запасенной в измерительном механизме, I- величина тока, протекающего по катушке.

Если катушка имеет n витков, длина и ширина катушки соответственно l и b, магнитная индукция пронизываюшая катушку –В уравнение для потокосцепления в полном виде можно записать как:

или где S активная площадь катушки.

Подставив эти уравнения в уравнение для статики получим:

После подстановки имеем:

Тогда установившийся угол отклонения aу можно записать как:

или

где S_п— чувствительность прибора.

Уравнение шкалы показывает, что шкала магнитоэлектрического измерительного механизма — линейна.

Следует отметить, что подвижная часть магнитоэлектрического механизма обладает относительно большим моментом инерции. Поэтому при включении в цепь переменного синусоидального тока, среднее значение которого за период равно нулю, средний вращающий момент также

равен нулю. Следовательно, данный механизм, примененный непосредственно может измерять только постоянные токи.

Магнитоэлектрический механизм логометрического типа.