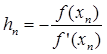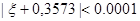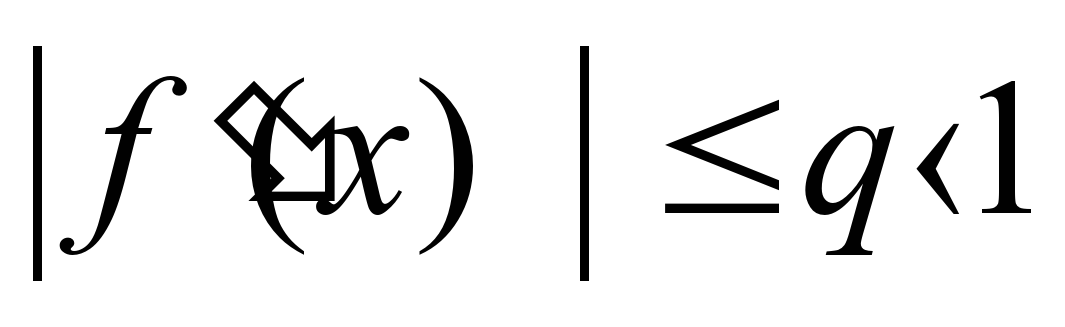| Название: Приближенное решение алгебраических и трансцендентных уравнений Метод Ньютона Раздел: Рефераты по математике Тип: реферат Добавлен 04:59:04 04 января 2011 Похожие работы Просмотров: 261 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||
| n | xn | f(xn) | f'(xn) | hn |
| 0 | 0 | 1 | 3 | -0,333333333 |
| 1 | -0,3 33333333 | 0,062142078 | 2,606445364 | -0,023841696 |
| 2 | -0,357 175029 | 0,000392296 | 2,573426701 | -0,000152441 |
| 3 | -0,35732747 0 | 1,63265E-08 | 2,573213436 | -6,34481E-09 |
| 4 | -0,357327477 | 2,9976E-15 | 2,573213427 | -1,16493E-15 |
| 5 | -0,357327477 | 0 | 2,573213427 | 0 |
Вывод: в третьем приближении получен результат с 4-мя точными знаками после запятой: 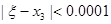
Ответ:
Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Список литературы
· «Основы вычислительной математики», Б. П. Демидович, И.А. Марон, 1966г.
Видео:Метод половинного деления решение нелинейного уравненияСкачать

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
БИК Курс лекций по дисциплине «Численные методы»
для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем
Раздел 2. Численные методы
2.1.1. Приближенные решения алгебраических и трансцендентных уравнений
Алгебраические и трансцендентные уравнения
Графический метод решения уравнений
1. Алгебраические и трансцендентные уравнения
При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

где 
В общем случае нелинейное уравнение можно записать в виде:
F ( x ) определена и непрерывна на конечном или бесконечном интервале 
Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.
Всякое число 

Число 

F ( 


Однократный корень называется простым.
Решить уравнение – значит найти множество всех корней этого уравнения.
Оно может быть конечным или бесконечным.
Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.
В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.
Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .
Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:
где a 0, a 1, . , a n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.
Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.
В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.
Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).
Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.
Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.
При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.
Решить уравнение – это значит
установить, имеет ли оно корни,
и найти значение корней с заданной точностью.
Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:
отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,
и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.
Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).
2. Графические методы решения уравнений
Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.
Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).
После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х0, ординаты обоих графиков в этой точке равны между собой, т. е. f (х0) = g (х0). Из этого равенства следует, что х0 – корень уравнения (рис. 2).

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.
Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)


Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).
Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.
Перепишем уравнение следующим образом: lg х = Зх — 5.
Функции в левой и в правой части уравнения имеют общую область определения: интервал 0
Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x 1 





Пример 3. Найти графически корни уравнения 2 х = 2х.
Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х 1 = 1 и х 2 = 2. Данное уравнение имеет два корня х 1 = 1 и х 2 = 2 (рис. 6).
Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.
1. Представить указанное уравнение в виде 

2. На бумаге вычертить графики функций у =
3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.
Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.
Корень 
Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.
Отделение корней можно произвести двумя способами – графическим и аналитическим.
Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.
Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.
Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.
Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.
1) Если непрерывная на отрезке 
2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке 
Рассмотрим примеры поведения некоторых функций:


Для отделения корней можно эффективно использовать ЭВМ.
П

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.
Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X 1 и X 2 (Концов выделенных отрезков).
Видео:Решение систем уравнений методом подстановкиСкачать

Решение алгебраических и трансцендентных уравнений приближенными методами
Существуют формулы и правила для нахождения решений уравнений третей и четвертой степени, но эти формулы громоздкие и не удобные в применении, особенно в практических задачах. Если рассмотреть не алгебраические уравнения, то задача усложняется еще больше, потому что получить формулу для нахождения корней такого уравнения практически невозможно.
Трансцендентные уравнения – это уравнения в которых переменная x находится в нутрии тригонометрических функций, показательных, логарифмических функций.
Если записать уравнение в виде f(x)=0 , то известные алгоритмы обычно не накладывают не каких ограничений на конкретный вид функций f(x), чтобы найти корни такого уравнения, т. е. те значения x которые обращают уравнения тождества, необходимо подобрать численный метод этого решения, численный метод как правило дает приближенное значение.
Если имеется нелинейное уравнение , то в процессе приближенного отыскания обычно выделяют два этапа:
- отделение корня;
- уточнение корня.
Под отделение корня понимается определение промежутка содержащего один и только один корень. Вторая точка находится в зависимости от заданной точности и условия задачи, чаще всего процесс отделения корня уравнения не может быть алгоритмизирован, существуют только некоторые классы уравнений для которых разработаны специальные приемы позволяющие отделять корень. Эти приемы могут быть аналитические или графические.
Просмотр содержимого документа
«Решение алгебраических и трансцендентных уравнений приближенными методами »
ГБОУ СПО САМАРСКИЙ СОЦИАЛЬНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ
практического занятия №5-6
Решение алгебраических и трансцендентных уравнений приближенными методами
Автор-составитель: Родионова Т.В.
По дисциплине: «Численные методы»
Тип урока: практическое занятие
Тема. Решение алгебраических и трансцендентных уравнений приближенными методами.
Формировать умения решить алгебраические уравнения приближёнными методами.
Учить использовать логические приёмы активизации мыслительной деятельности.
Развивать алгоритмическое мышление.
Проверить уровень знаний некоторых методов приближённого решения уравнений.
Воспитывать вычислительную культуру, внимательность, аккуратность, дисциплинированность.
Развивать познавательный интерес, навыки самоконтроля, умения работать с тестом смешанного типа.
Оборудование: доска, планшеты функций, карточки с заданием (тест).
Орг. момент. (5 мин)
Целевая установка и актуализация знаний. (5 мин)
Решение уравнений(20 мин)
Самостоятельная работа студентов (тест). (10 мин)
Подведение итогов урока. Домашнее задание (5 мин)
Приветствие, проверка присутствующих. Сегодня на уроке мы рассмотрим пример применения метода итераций для решения алгебраических уравнений. Вспомним алгоритм решения и численные, приближённые методы решения уравнений. В конце урока выясним, как каждый знает основные положения темы с помощью мини-теста.
II. Актуализация знаний.
Что называется уравнением?
Что является корнем уравнения?
Какие уравнения называют трансцендентными, и какие — алгебраическими?
Что значит непрерывная функция, приведите пример?
Вспомним алгоритм решения алгебраических и трансцендентных уравнений. Из скольких этапов он состоит.
В каком случае говорят, что корень отделён?
Метод проб с десятичным делением
Метод проб с половинным делением
аким способом может быть отделён корень?
-Назовите методы уточнения корня.
-Чем похожи, и чем отличаются метод проб с десятичным делением и метод проб с половинным делением?
-Охарактеризуйте кратко остальные методы.
III. Решение уравнений.
1.На прошлом занятии мы рассмотрели теоретический блок метода итераций. Сейчас рассмотрим конкретный пример.
Пусть корень уравнения отделён и принадлежит интервалу [0,1; 0,2].
Для уточнения корня применим метод итераций. Представим уравнение в виде, удобном для применения метода
Проверим условия применимости метода. Найдем производную и сравним модуль её значения на заданном отрезке с1.
Пусть х = 0,15, тогда f ‘(0,15) =-0,005625
Получили |-0,005625| f ‘(х) | значит, метод итераций применить можно.
Примем за начальное приближение любое число из данного интервала.
х0≈0,16 и будем вычислять последовательные приближения
Получили приближённое значение корня и ответ.
IV. Самостоятельная работа студентов (тест).
(см. Приложение 1.)
V. Подведение итогов урока. Домашнее задание.
1.Решить комбинированным методом проб и хорд с точностью до 0,001:
х 5 +0,2х-0,84=0, (положительный корень). (Отв.0,919)
2. Решить комбинированным методом хорд и касательных с точностью до 0,001:
х 6 +2х-1=0, (положительный корень). (Отв.0,493)
3.*Составить алгоритм и программу для нахождения приближенных решений алгебраических и (или) трансцендентных уравнений.
(см. Приложение 2.)
1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.
2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.
3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.
4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.
Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»
Вариант для преподавателя Вариант №1
Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.
Установите соответствие понятия определению:
1. Численные методы
2. Корень уравнения
3. Скорость сходимости
А) – это характеристика близости приближённого решения к точному решению при некоторых дополнительных ограничениях.
Б) позволяют получить численный ответ с помощью последовательности осуществимых численных операций.
В). – число, при подстановке которого в уравнение, получается верное равенство.
Установите соответствие уравнения его виду:
А
Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.
Среди предложенных функций выберите непрерывную:
А) у = 5х 4 -7х 2 +4х+10, Б) у = tg х,
В) у = 18 / х, Г) у = 5 / (х-1).
Решить уравнение х 4 -25х 2 +144=0
и выбрать правильный ответ.
Метод итераций можно применять для решения алгебраического уравнения, если:
Б) | f ‘(x)| 1 на отрезке [a,b];
Г) | f ‘(x)| 0 на отрезке [a,b].
Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.
Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то применяется формула………..
Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то
х0 =b и применяется формула………..
Найти приближённое значение корня уравнения
х 3 +х 2 -3=0 на отрезке [1;1,5]., применяя метод хорд и метод касательных, с точностью до 0,01.
Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»
Вариант для преподавателя Вариант №2
Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.
Установите соответствие понятия определению:
1. Открытый интервал
2. Условие сходимости метода
3. Численные методы
А) — раздел математики, в котором разрабатываются численные методы решения задач.
Б) — это минимальные по возможности ограничения, при которых приближённое решение задачи стремится к точному решению.
В) – совокупность всех действительных чисел х , удовлетворяющих неравенству: а х b, где а и b – данные числа. Обозначается так (а,b).
Установите соответствие уравнения его виду:
А) sin 3 х = 2cosх; Б
Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.
Среди предложенных функций выберите непрерывную:
А) у =, сtg х; Б) у = 3х 4 -5х 2 +2х+9;
В) у = 8 / х; Г) у = 15 / (х-2).
Решить уравнение х 4 — 13х 2 +36=0
и выбрать правильный ответ.
В процессе решения алгебраического уравнения отделение корня можно выполнить следующими способами:
А) практически; Б) аналитически;
В) графически; Г) на глаз.
Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.
Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то
х0 =b и применяется формула………..
Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то применяется формула………..
Найти приближённое значение корня уравнения
х 3 -2х-1=0 на отрезке [1,5;2]., применяя метод десятичного деления и метод проб, с точностью до 0,01.
Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»
Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.
Установите соответствие понятия определению:
1. Численные методы
2. Корень уравнения
3. Скорость сходимости
А) – это характеристика близости приближённого решения к точному решению при некоторых дополнительных ограничениях.
Б) позволяют получить численный ответ с помощью последовательности осуществимых численных операций.
В). – число, при подстановке которого в уравнение, получается верное равенство.
Установите соответствие уравнения его виду:
А
Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.
Среди предложенных функций выберите непрерывную:
А) у = 5х 4 -7х 2 +4х+10, Б) у = tg х,
В) у = 18 / х, Г) у = 5 / (х-1).
Решить уравнение х 4 -25х 2 +144=0
и выбрать правильный ответ.
Метод итераций можно применять для решения алгебраического уравнения, если:
Б) | f ‘(x)| 1 на отрезке [a,b];
Г) | f ‘(x)| 0 на отрезке [a,b].
Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.
Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то применяется формула………..
Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то
х0 =b и применяется формула………..
Найти приближённое значение корня уравнения
х 3 +х 2 -3=0 на отрезке [1;1,5]., применяя метод хорд и метод касательных, с точностью до 0,01.
Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»
Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.
Установите соответствие понятия определению:
1. Открытый интервал
2. Условие сходимости метода
3. Численные методы
А) — раздел математики, в котором разрабатываются численные методы решения задач.
Б) — это минимальные по возможности ограничения, при которых приближённое решение задачи стремится к точному решению.
В) – совокупность всех действительных чисел х , удовлетворяющих неравенству: а х b, где а и b – данные числа. Обозначается так (а,b).
Установите соответствие уравнения его виду:
А) sin 3 х = 2cosх; Б
Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.
Среди предложенных функций выберите непрерывную:
А) у =, сtg х; Б) у = 3х 4 -5х 2 +2х+9;
В) у = 8 / х; Г) у = 15 / (х-2).
Решить уравнение х 4 — 13х 2 +36=0
и выбрать правильный ответ.
В процессе решения алгебраического уравнения отделение корня можно выполнить следующими способами:
А) практически; Б) аналитически;
В) графически; Г) на глаз.
Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.
Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то
х0 =b и применяется формула………..
Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то применяется формула………..
Найти приближённое значение корня уравнения
х 3 -2х-1=0 на отрезке [1,5;2]., применяя метод десятичного деления и метод проб, с точностью до 0,01.
Практическая работа № 5
Приближенное решение алгебраического уравнения комбинированным методом
Содержание работы. Отыскание корня алгебраического уравнения комбинированным методом (методом проб и хорд или методом хорд и касательных).
Тип задания. Дано алгебраическое уравнение степени выше второй f(x)=0. Даются указания, какой именно корень требуется найти. Ставится задача отыскания приближенного значения корня с заданной точностью.
1. Графически отделить корень данного уравнения: найти отрезок [а; b] достаточно малой длины, внутри которого содержится искомый корень, и этот корень единственный.
Проверить аналитически, что:
Методом проб уточнить корень, добившись того, что длина отрезка [а; b] станет равной 0,1.
Избрать один из рекомендуемых комбинированных методов, составить расчетный бланк для записи вычислений.
Провести вычисления в соответствии с разработанной схемой.
Проверить полученный результат путем подстановки найденного корня в уравнение.
Задание 1. Вычислить наименьший положительный корень уравнения
2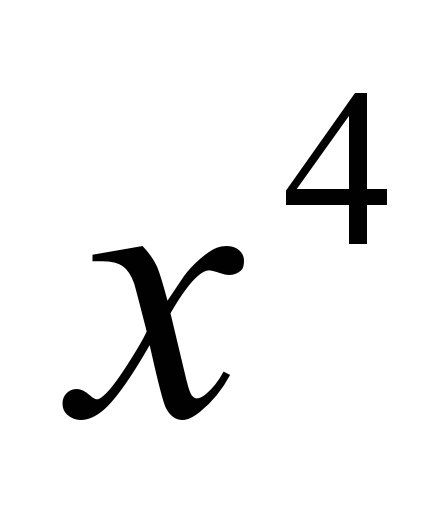
комбинированным методом проб и хорд с точностью до четвертого десятичного знака.
Задание 2. Вычислить наименьший положительный корень уравнения
2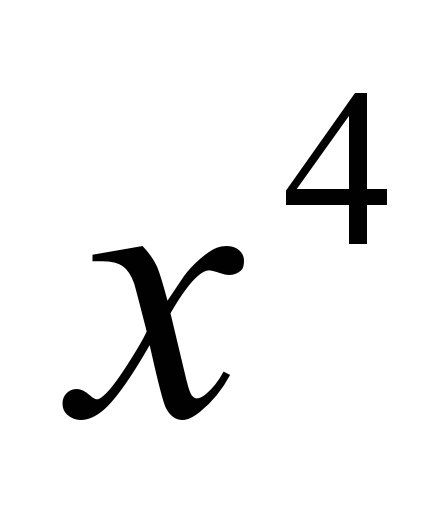
комбинированным методом хорд и касательных.
1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.
2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.
3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.
4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.
Практическая работа №6*.
Приближенное решение трансцендентного уравнения
Тип задания. Найти корень данного уравнения F(x)=0 с заданной точностью одним из методов: 1) комбинированным методом проб и хорд;
2) комбинированным методом хорд и касательных;
3) методом итераций.
Если решено применить метод (1) или (2), то порядок выполнения работы тот, который изложен в работе № 5. Заметим лишь, что при выполнении данной работы следует пользоваться таблицами тех трансцендентных функций, которые содержат в уравнении (логарифм, тригонометрические функции и др.).
Приведем план выполнения данной работы в случае применения метода итераций.
Графически или другим методом найти грубое приближенное значение корня 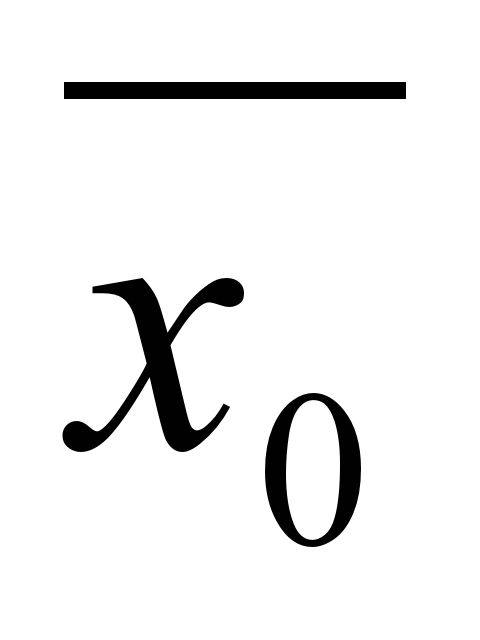
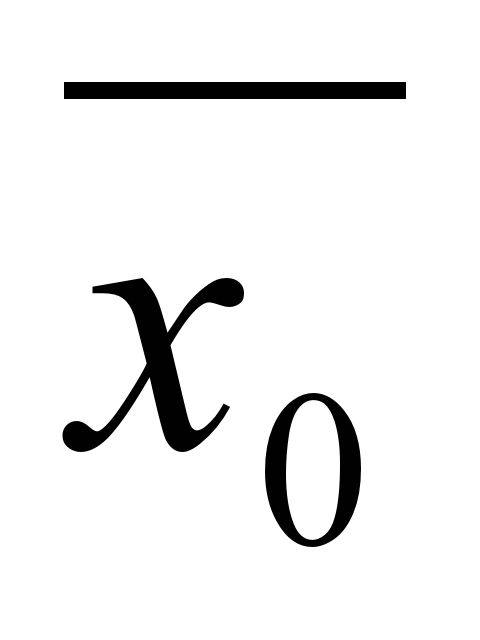
Привести данное уравнение F (х) = 0 к виду x = f (x). Из различных представлений уравнения в этом виде выбрать такое, при котором 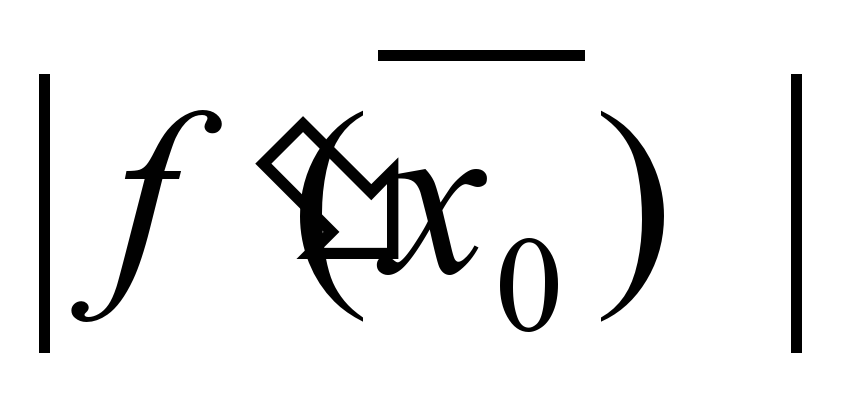
Убедиться в том, что для всех х отрезка [а; b] выполняется неравенство
где q—малое число, значительно меньшее единицы. (Если 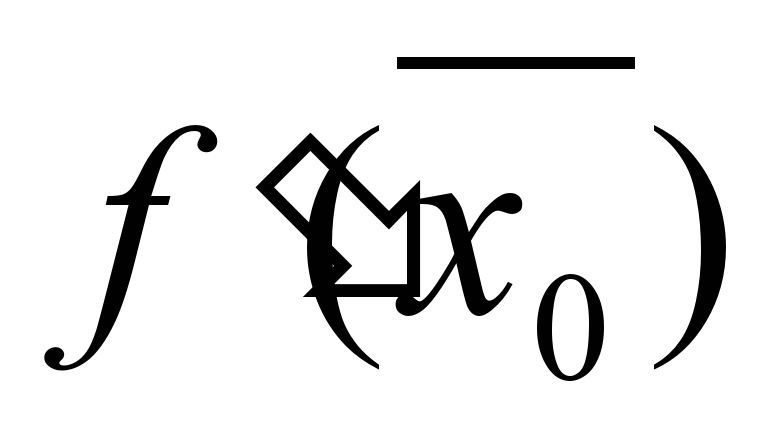
Составить расчетный бланк для вычисления последовательных приближений, приняв за начальное приближение 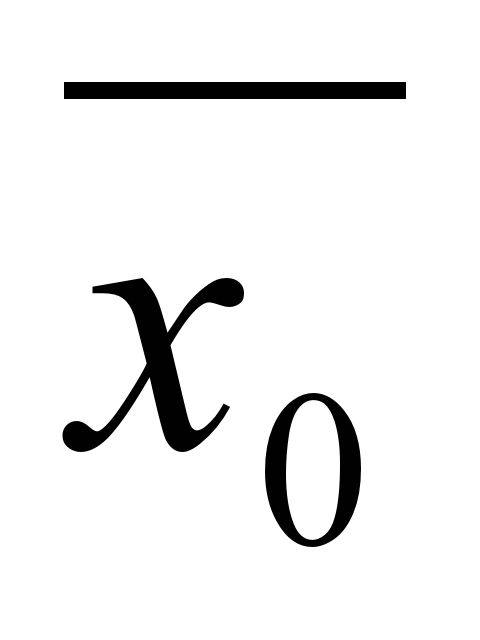
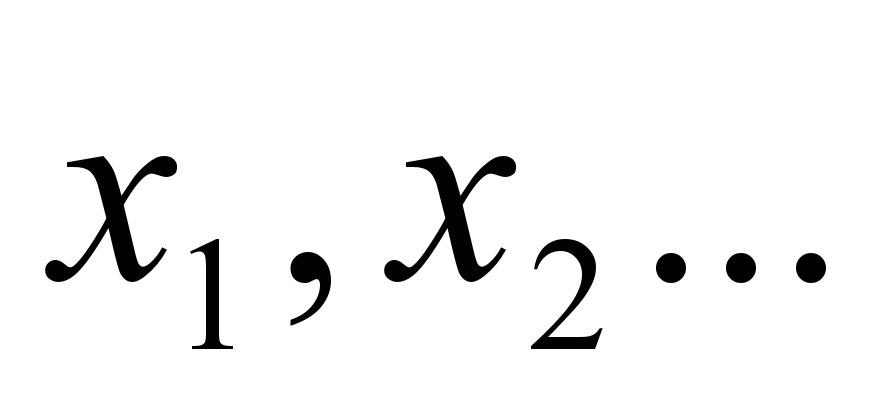
Если окажется необходимым, произвести дополнительную оценку точности найденного корня.
Задание. Вычислить корень уравнения lg x+5x—2=0 с точностью до 0,0001 методом итераций.
1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.
2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.
3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.
4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.
📹 Видео
Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Метод итераций (последовательных приближений)Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод итерацийСкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать




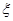 уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при
уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при 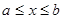 . Найдя какое-нибудь n-e приближение корня
. Найдя какое-нибудь n-e приближение корня 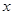 n
n 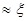 (
(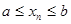 ), мы можем уточнить его по Методу Ньютона следующим образом. Пусть
), мы можем уточнить его по Методу Ньютона следующим образом. Пусть 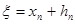 , где hn малая величина. Отсюда, применяя формулу Тейлора, получим:
, где hn малая величина. Отсюда, применяя формулу Тейлора, получим: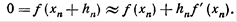
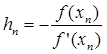
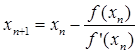 (n=0,1,2…).
(n=0,1,2…).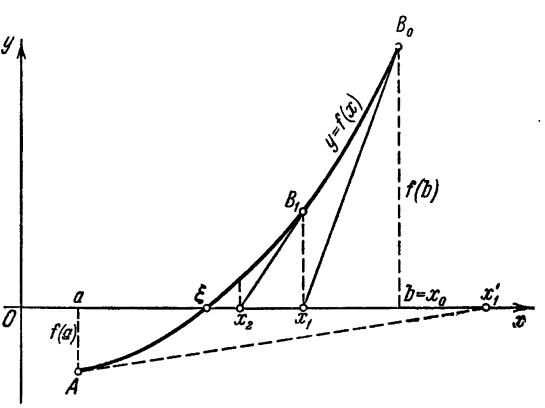
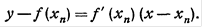
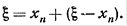
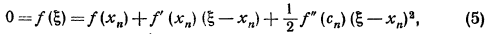
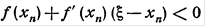
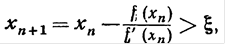
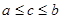 .
.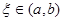 .
.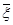 функции f ( x ) такому, что
функции f ( x ) такому, что 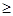 а. Так как в силу положительности производной f ‘ (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +
а. Так как в силу положительности производной f ‘ (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +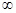 ), то
), то 
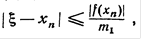 (6)
(6)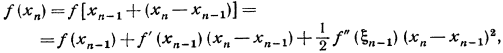 (7)
(7)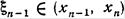 .Так как в силу определения приближения хп имеем
.Так как в силу определения приближения хп имеем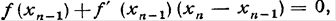

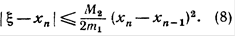
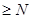 имеем:
имеем: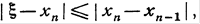
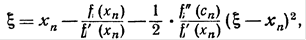
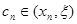 . Отсюда, учитывая формулу (3), будем иметь:
. Отсюда, учитывая формулу (3), будем иметь: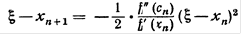
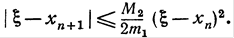 (9)
(9)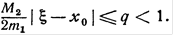
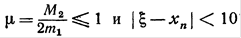
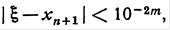
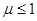 , то с помощью метода Ньютона число верных знаков после запятой искомого корня
, то с помощью метода Ньютона число верных знаков после запятой искомого корня 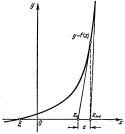
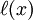 , значения которой совпадают со значениями f (x ) в двух фиксированных точках, в данном случае — в точках xi − 1 и xi .)
, значения которой совпадают со значениями f (x ) в двух фиксированных точках, в данном случае — в точках xi − 1 и xi .)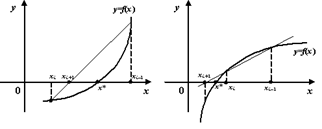
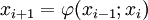 . Найдём выражение для функции
. Найдём выражение для функции 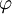 .
.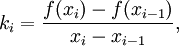
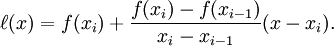
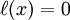 , находим
, находим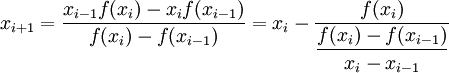
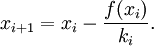 (1)
(1)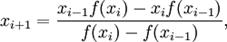
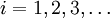 , начиная с двух приближений x 0 и x 1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x 0 и x 1 (и что значения функции f в точках x 0 и x 1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство
, начиная с двух приближений x 0 и x 1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x 0 и x 1 (и что значения функции f в точках x 0 и x 1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство 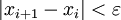 , где
, где 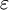 — желаемая точность нахождения корня. При этом полагают приближённое значение корня равным
— желаемая точность нахождения корня. При этом полагают приближённое значение корня равным 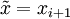 .
.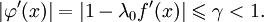 Это неравенство может быть переписано в виде
Это неравенство может быть переписано в виде 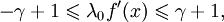 откуда получаем, что сходимость гарантируется, когда, во-первых,
откуда получаем, что сходимость гарантируется, когда, во-первых, 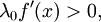 так как
так как 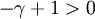 (тем самым проясняется смысл выбора знака числа
(тем самым проясняется смысл выбора знака числа 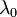 ), а во-вторых, когда
), а во-вторых, когда 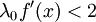 при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если
при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если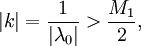
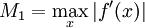 . Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
. Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
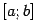 и знаки
и знаки  и
и 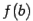 различны (функция
различны (функция 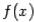 меняет знак при переходе через корень
меняет знак при переходе через корень 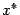 ).
).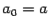 и
и  и вычислим значения функции в левом конце отрезка,
и вычислим значения функции в левом конце отрезка, 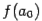 , и в его середине
, и в его середине 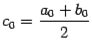 ;
; 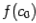 . Сравним знаки чисел
. Сравним знаки чисел 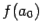 и
и 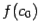 . Если эти знаки различны, то корень
. Если эти знаки различны, то корень 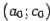 ; если же одинаковы, то тогда различны знаки
; если же одинаковы, то тогда различны знаки 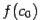 и
и 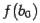 , и корень лежит в интервале
, и корень лежит в интервале 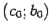 . (Возможен ещё случай
. (Возможен ещё случай 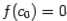 ; тогда корень
; тогда корень 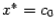 уже найден.) В обоих случаях смены знака корень оказывается отделён на отрезке
уже найден.) В обоих случаях смены знака корень оказывается отделён на отрезке 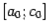 либо
либо 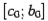 , длина которого ровно в два раза меньше длины исходного отрезка
, длина которого ровно в два раза меньше длины исходного отрезка 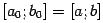 . Обозначим этот отрезок половинной длины через
. Обозначим этот отрезок половинной длины через 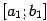 (то есть положим
(то есть положим 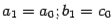 в случае, когда
в случае, когда 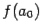 и
и 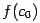 разных знаков, и
разных знаков, и 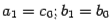 в случае, когда
в случае, когда 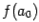 и
и  : снова отыщем его середину
: снова отыщем его середину 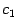 , найдём значение функции
, найдём значение функции 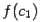 и сравним знак этого числа со знаком
и сравним знак этого числа со знаком 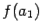 ; если знаки разные, то корень отделён на
; если знаки разные, то корень отделён на 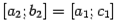 , если одинаковые, то на
, если одинаковые, то на 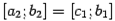 (или же оказывается, что
(или же оказывается, что 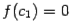 ; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.
; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.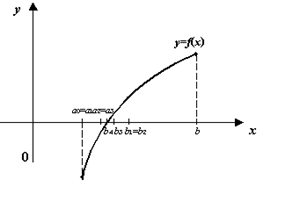
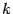 делений длина отрезка, на котором лежит корень, сокращается в
делений длина отрезка, на котором лежит корень, сокращается в 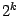 раз и становится равной
раз и становится равной 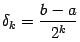 (если корень не был точно определён на каком-то предыдущем этапе, то есть не совпал с
(если корень не был точно определён на каком-то предыдущем этапе, то есть не совпал с 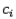 при некотором
при некотором 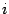 ).
).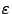 — заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство
— заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство 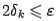 . Очевидно, что если при этом положить
. Очевидно, что если при этом положить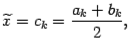
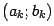 , до середины этого интервала
, до середины этого интервала 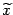 будет не больше
будет не больше 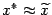 будет выполнено с нужной точностью. C увеличением точности заметно возрастает объем вычислительной работы, поэтому метод удобно применять для нахождения грубого корня уравнения.
будет выполнено с нужной точностью. C увеличением точности заметно возрастает объем вычислительной работы, поэтому метод удобно применять для нахождения грубого корня уравнения.
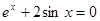 ,
, 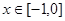 .
.
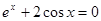
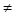 0 при
0 при