Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение:
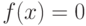 | ( 4.1) |
Необходимо решить это уравнение, т. е. найти его корень 
Если функция имеет вид многочлена степени m,
где ai — коэффициенты многочлена, 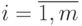
Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .
Такие уравнения обычно имеют бесконечное множество решений.
Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .
Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.
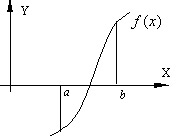
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).
Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
- отделение корней, — т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
- уточнение корней, — т.е. сужение интервала [a,b] до величины равной заданной степени точности
.
Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
Видео:10 Численные методы решения нелинейных уравненийСкачать

Последовательность действий
Лабораторная работа №4
Тема. Приближенные методы решения нелинейных уравнений
Задание.
Решить нелинейное уравнение с заданной точностью e ,
двумя приближёнными (итерационными) методами:
1. методом половинного деления (все студенты)
2. методом, выбранным в соответствии с вариантом.
Вид уравнения и метод выбрать в соответствии с вариантом (приложение 1).
Порядок выполнения
1. Первый этап – этап локализация корней
· Определите область допустимых значений (ОДЗ) функции y=f(x).
· Определите количество действительных корней уравнения (1.1) и их расположение. Для этого протабулируйте функцию y=f(x) на достаточно большом отрезке [а, b] из ОДЗ с шагом h=(b-a)/10 и постройте её график (рис.1.1).
· Выделите отрезки, на которых существует единственный корень, используя теорему из математического анализа.
Теорема 1. Уравнения (1.1) имеет единственный корень в интервале x * Î (а, b), если функция у=f(x) удовлетворяет на отрезке xÎ [a, b] следующим условиям:
1. функция непрерывна,
2. f(a) f(b) ’ (x) сохраняет знак на этом отрезке.
· Определите нулевое приближение (нулевую итерацию) х0 для метода хорд и метода касательных.
· Протабулируйте функцию на отрезке, на котором существует единственный корень, и постройте ее график.
2. Второй этап – этап уточнения корня (этап построения итерационного процесса) до заданной точности
Для построения итерационного процесса используйте одну из приведенных ниже расчетных схем в зависимости от метода решения нелинейного уравнения (рис. 1.2, 1.3 и 1.4).
Рис.1.2 Расчетная схема метода половинного деления
Для формирования концов сужающегося отрезка [a, b] в методе половинного деления рекомендуется использовать логическую функцию Excel ЕСЛИ.
Рис.1.3. Расчетная схема метода хорд
Рис.1.4. Расчетная схема метода касательных
3. Условное форматирование
Условное форматирование–это форматирование выделенных ячеек на основе некоторого критерия, в результате чего произойдет цветовое оформление ячеек, содержимое которых удовлетворяет заданному условию.
Чтобы сделать наглядным окончание итерационного процесса, воспользуйтесь Условным форматированием. Для этого выполните следующие действия:
· выделите ячейки последнего столбца расчетной схемы, где будет задаваться критерий окончания итерационного процесса (рис. 1.2, или 1.3, или 1.4);
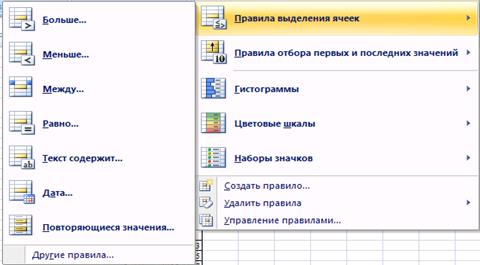
· на вкладке Главная выберите панель Стили и нажмите кнопку Условное форматирование;
· в появившемся меню (рис.1.5) выберите пункт Правила выделения ячеек, а в подменю – пункт Меньше;
Рис.1.5. Установка параметров условного форматирования
· в левой части открывшегося диалогового окна Меньше (рис.1.6) задайте значение, которое будет использовано в качестве критерия (в нашем примере это адрес ячейки Е4 для всех трех расчетных схем, где находится значение точности ε).
· в выпадающем списке правой части окна выберите цвет, которым будут окрашены ячейки, отвечающие заданному условию; и нажмите кнопку ОК.
Рис.1.6. Диалоговое окно условного форматирования
В результате условного форматирования наглядно видно (рис.1.2, 1.3 и 1.4)., что решением нелинейного уравнения (1.1) с точностью e=0,01 является:
| Приближенное значение корня | Номер итерации | Метод |
| Х * ≈1,763 | n=3 | касательных |
| Х * ≈1,759 | n=3 | хорд |
| Х * ≈1,758 | n=8 | половин.деления |
4. Исследовательская часть (численный эксперимент)
· Постройте таблицу и диаграмму зависимости количества итераций от заданной точности n=n(e) для e=0.1; 0.01; 0.001; 0.0001.
· Проанализируйте полученные результаты, сделайте соответствующие выводы.
5. Контрольный пример
Решите ваше нелинейное уравнение, используя надстройку Подбор параметра.
Последовательность действий
1. 

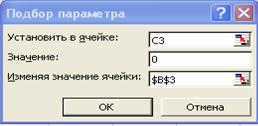
2. Выберите вкладку Данные, на панели Работа с данными нажмите кнопку Анализ «что-если» и в открывшемся подменю выберите пункт Подбор параметра.
Рис.1.8. Окно «Подбор параметра»
3. В появившемся окне «Подбор параметра»сделайте установки, как показано на рис.1.8 и нажмите кнопку ОК.
Если все было проделано правильно, то в ячейке В3 (рис.1.7) будет получено приближенное значение корня нашего уравнения.
Проделайте все эти операции ещё раз с другим значением начального приближения х0., для определения других корней уравнения (если они имеются).
1. Какое уравнение называется нелинейным. Пример нелинейного уравнения.
2. Что является решением нелинейного уравнения.
3. Геометрическая интерпретация решения нелинейного уравнения.
4. Методы решения нелинейного уравнения (прямые и итерационные), в чем разница.
5. Два этапа решения нелинейного уравнения. Какие задачи ставятся на первом и втором этапах.
6. Табулирование функции, сеточная функция, шаг табулирования.
7. Построение итерационной последовательности. Понятие сходимости итерационной последовательности. Нахождение приближенного значения корня нелинейного уравнения с заданной точностью ε.
8. Критерии окончания итерационного процесса. Геометрический смысл критериев.
9. Метод половинного деления. Суть метода (см. вопросы 6,7).
10. Метод Ньютона (касательных). Как выбирается нулевое приближение (нулевая итерация). Суть метода (см. вопросы 6, 7).
11. Метод хорд. Как выбирается нулевое приближение (нулевая итерация). Суть метода (см. вопросы 6, 7).
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Приближенные методы решения нелинейных уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
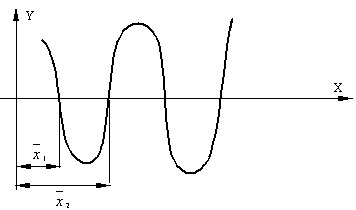
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
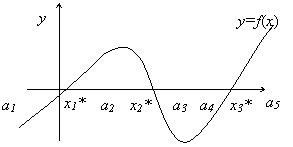
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 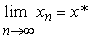
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 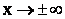
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1=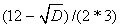
X2=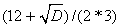
Так как f / (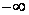
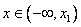
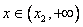
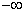
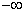
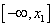
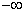
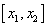
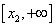
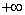
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при 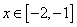
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 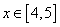
📺 Видео
Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

МЗЭ 2021 Лекция 9 Метод Ньютона для решения нелинейных уравненийСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод простой итерации Пример РешенияСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Метод половинного деления решение нелинейного уравненияСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Метод касательных (метод Ньютона)Скачать

1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

Метод итерацийСкачать

Лекция 2. Методы решения нелинейных уравнений. 18.02.2021Скачать


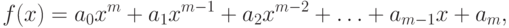
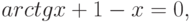

 .
.