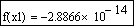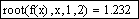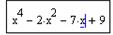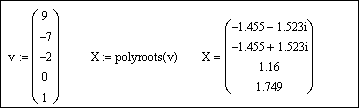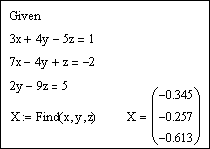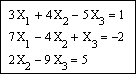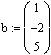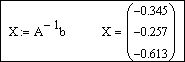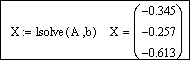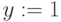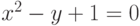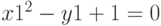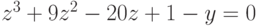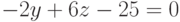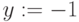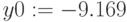Приближенное решение уравнений в маткаде

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

• отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
• уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

• f(x) – функция левой части уравнения f(x) = 0;
• x – переменная, относительно которой требуется решить уравнение;
• a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

1. задается матрица коэффициентов при неизвестных системы A;
2. задается столбец свободных членов b;
3. вводится формула для нахождения решения системы X:=A -1 b;
4. выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

1. Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
2. Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3. Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

1. В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
2. Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

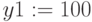
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

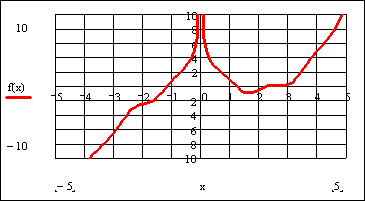
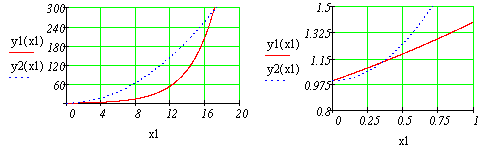
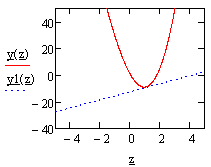
После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

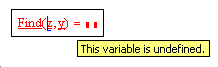
Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .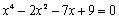

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 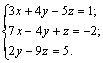Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Возможности математического пакета MathCad. Приближенные решения уравнений и их систем

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМ. М. Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

РЕФЕРАТ
Возможности математического пакета MathCad. Приближенные решения уравнений и их систем

студентка группы МДИ-117
Рыбкина В. А.

Видео:Mathcad-09. Пример: уравненияСкачать

Введение

При решении некоторых математических задач, при моделировании различных явлений, при автоматизации рабочего места пользователю приходится выбирать ту среду, которая бы позволяла реализовать с наибольшим комфортом многие варианты решений. До недавнего времени исследователю приходилось разрабатывать на основе алгоритма свои программные средства, пользуясь известными языками программирования. В настоящее время появилось много пакетов прикладных программ, в которых за счет встроенного процессора можно, легко освоив правила работы данной среды, проводить построение различных моделей, решать сложные математические задачи и находить значения выражений.

Система MathCad – пакет, предназначенный для проведения математических расчетов, который содержит текстовый редактор, вычислитель и графический процессор. Фирма MathSoft Inc (США) выпустила первую версию системы в 1986 г. Главная отличительная особенность системы MathCad заключается в её входном языке, который максимально приближён к естественному математическому языку, используемому как в трактатах по математике, так и вообще в научной литературе.

От других продуктов аналогичного назначения MathCad отличается ориентацией на создание высококачественных документов (докладов, отчетов, статей) в режиме WYSIWYG (What You See Is What You Get). Это означает, что, внося изменения, пользователь немедленно видит их результаты и в любой момент может распечатать документ во всем блеске. Преимущества MathCad состоит в том, что он не только позволяет провести необходимые расчеты, но и оформить свою работу с помощью графиков, рисунков, таблиц и математических формул. А эта часть работы является наиболее рутинной и мало творческой, к тому же она и время емкая и малоприятная.

Видео:Приближенное решение систем уравнений в MathCAD 14 (30/34)Скачать

1. Основные возможности математического пакета MathCad

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

1.1 Общая характеристика MathCad

Система MathCad содержит текстовый редактор, вычислитель и графический процессор.

Текстовый редактор служит для ввода и редактирования текстов. Текст может состоять из слов, математических выражений и формул, спецзнаков. Отличительная черта системы – это использование общепринятой в математике символики (деление, умножение, квадратный корень).

Вычислитель обеспечивает вычисление по сложным математическим формулам, имеет большой набор встроенных математических функций, позволяет вычислять ряды, суммы, произведения, определенный интеграл, производные, работать с комплексными числами, решать линейные и нелинейные уравнения, проводить минимизацию функции, выполнять векторные и матричные операции и т. д. Легко можно менять разрядность чисел и погрешность интеграционных методов.

Графический процессор служит для создания графиков. Он сочетает простоту общения с пользователем с большими возможностями графических средств. Графика ориентирована на решение типичных математических задач. Возможно быстрое изменение размеров графиков, наложение их на текстовые надписи и перемещение их в любое место документа.

Многие задачи, решаемые с помощью математических пакетов, сводятся к решению уравнений – алгебраических, степенных, тригонометрических, к поиску значений неизвестных, превращающих эти уравнения в тождества строго или приближенно. Успех в решении подобных задач зависит не только от мощности соответствующих инструментов, встроенных в MathCad , но и от знания пользователем их особенностей, нюансов, сильных и слабых сторон.

Задачи, решаемые в MathCad:

1) Подготовка научно-технической документации, содержащей текст и формулы в привычной для специалиста форме;

2) Вычисления результатов математических операций с константами, переменными и размерными физическими величинами;

3) Векторные и матричные операции;

4) Решение уравнений и систем уравнений;

5) Статистические расчеты и анализ данных;

6) Построение графиков;

7) Аналитические преобразования и аналитическое решение уравнений и систем;

8) Аналитическое и численное дифференцирование и интегрирование;

9) Решение дифференциальных уравнений.

Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

1.2 Структура программы MathCad

Основное окно приложения имеет ту же структуру, что и большинство

приложений Windows. Сверху вниз располагаются заголовок окна, строка меню, панели инструментов (стандартная и форматирования) и рабочий лист,

или рабочая область, документа. Новый документ создается автоматически при запуске MathCad. Файлы документов в MathCad имеют расширение .mcd.

Большинство команд можно выполнить как с помощью меню (верхнего или контекстного), так и панелей инструментов или клавиатуры. Панель Math (Математика) предназначена для вызова на экран еще девяти панелей, с помощью которых происходит вставка математических операций в документы. Чтобы вызвать какую-либо из них, нужно нажать соответствующую кнопку на панели Математика.

В окне редактирования формируется документ MathCad. Новый документ получает имя Untitled (Без названия) и порядковый номер. Одновременно открыто может быть до восьми документов.

Документ состоит из трех видов областей: формульных, текстовых и графических. Расположение нетекстовых блоков в документе имеет принципиальное значение. Области просматриваются системой, интерпретируются и исполняются. Просмотр идет слева направо и сверху вниз.

Для ввода текстового комментария нужно выполнить команду Text Region (Текстовая область) из пункта меню Insert или нажать клавишу с двойной кавычкой (“), или нажать на кнопку текста на панели инструментов. Текстовая область служит для размещения текста между формулами и графиками. При этом в месте ввода появляется курсор в виде вертикального штриха, на место которого вводятся символы текста. Внутри текста курсор перемещается клавишами перемещения курсора. Переход на новую строку производится нажатием на клавишу Enter. Для окончания ввода нужно щелкнуть мышью вне текстовой области.

Для ввода формулы нужно установить указатель мыши в свободном месте окна редактирования и щелкнуть левой кнопкой мыши. Появится визир в виде красного крестика. Он указывает место, с которого начинается набор формулы.

Константами называются поименованные объекты, хранящие некоторые значения, которые не могут быть изменены.

В MathCad применяются десятичные, восьмеричные и шестнадцатеричные числовые константы. Десятичные константы могут быть целочисленными, вещественными, заданными с фиксированной точкой, и вещественными, заданными в виде мантиссы и порядка.

В MathCad содержится особый вид констант – размерные. Помимо своего числового значения они характеризуются еще и указанием на то, к какой физической величине они относятся. Для этого указания используется символ умножения. В системе MathCad заданы следующие основные типы физических величин: time (время), length (длина), mass (масса) и charge (заряд). При необходимости их можно изменить на другие.

Переменные являются поименованными объектами, которым присвоено некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы MathCad должны начинаться с буквы и могут содержать следующие символы:

1) латинские буквы любого регистра;

2) арабские цифры от 0 до 9;

3) символ подчеркивания (_), символ процент (%) и символ (.);

4) буквы греческого алфавита (набираются с использованием клавиши Ctrl или применяется палитра греческих букв).

Переменные должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной. Попытка использовать неопределенную переменную ведет к выводу сообщения об ошибке. MathCad читает рабочий документ слева направо и сверху вниз, поэтому определив переменную, ее можно использовать в вычислениях везде правее и ниже равенства, в котором она определена.

Переменные могут использоваться в математических выражениях, быть аргументами функций или операндом операторов.

Переменные могут быть и размерными, т. е. характеризоваться не только своим значением, но и указанием физической величины, значение которой они хранят. Проведение расчетов с размерными величинами и переменными особенно удобно при решении различных физических задач.

Предопределенные (системные) переменные – особые переменные, которым изначально системой присвоены начальные значения.

Рисунок 1 Предопределенные переменные

Операторы – элементы языка, с помощью которых можно создавать математические выражения. Операторы, обозначающие основные арифметические действия, вводятся с панели Calculator (Калькулятор, Арифметика). Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus (Матанализ). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Результатом действия логических, или булевых, операторов являются только числа 1 (если логическое выражение, записанное с их помощью, истинно) или 0 (если логическое выражение ложно).

Видео:Пример решения уравнения в MathCAD 14 (33/34)Скачать

2. Приближенные решения уравнений и их систем в MathCad

Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

2.1 Особенности решения уравнений и их систем в MathCad

Алгоритм приближенного решения уравнения f(x)=0 состоит из двух этапов:

1. Нахождения промежутка, содержащего корень уравнения (или начальных приближений для корня);

2. Получения приближенного решения с заданной точностью с помощью функции root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид v₀+v₁x+…+v_n-1x n-1 + +v_nx n , лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.

Функция Polyroots(v) – возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома.

Решение систем уравнений матричным методом

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х₁, х₂, …, х_n:

Система линейных уравнений может быть записана в матричном виде: Ах = b, где:

Если det A ≠ 0 то система или эквивалентное ей матричное уравнение имеет единственное решение.

Системы линейных уравнений удобно решать с помощью функции lsolve. Функция lsolve(А, b) – возвращает вектор решения x такой, что Ах = b.

Решение системы уравнений методом Гаусса

Метод Гаусса, его еще называют методом Гауссовых исключений, состоит в том, что систему уравнений приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей. В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду, а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица. Последний, (n+1) столбец этой матрицы содержит решение системы.

В MathCad прямой и обратный ходы метода Гаусса выполняет функция rref(A).

Решение систем уравнений с помощью функций Find или Minner

Для решения системы уравнений с помощью функции Find необходимо выполнить следующее:

1. Задать начальное приближение для всех неизвестных, входящих в систему уравнений. MathCad решает систему с помощью итерационных методов;

2. Напечатать ключевое слово Given. Оно указывает MathCad, что далее следует система уравнений;

3. Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов , ≥ и ≤;

4. Введите любое выражение, которое включает функцию Find, например: х:= Find(х, у).

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блоком решения уравнений.

Функция Minner очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minner возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minner такие же, как и функции Find. Функция Minerr(x1, x2, . . .) – возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Символьное решение уравнений

Имеются некоторые задачи, для которых возможности MathCad позволяют находить решения в символьном (аналитическом) виде. Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:

• если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении;

• если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.

Команда Символы → Переменные → Вычислить позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

Видео:MathCAD. Given - FindСкачать

2.2 Решения уравнений и их систем в MathCad

Пример 1. Построить график функции f(x) и приблизительно определить один из корней уравнения. Решить уравнение f(x) = 0 с помощью встроенной функции MathCAD root.

Пример 2. Для полинома g(x) выполнить следующие действия:

1. С помощью команды Символы → Коэффициенты полинома создать

вектор V, содержащий коэффициенты полинома;

2. Решить уравнение g(x) = 0 с помощью функции polyroots;

3. Решить уравнение символьно, используя команду Символы →

Пример 3. Решить систему линейных уравнений:

1. Матричным способом и используя функцию lsolve;

2. Методом Гаусса;

3. Используя функцию Find.

Пример 4. Решить систему нелинейных уравнений с помощью функции Minerr .

Пример 5. Символьно решить системы уравнений.

Видео:Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать

Заключение

MathCad – это универсальная система, которая может использоваться в любой области науки и техники, везде, где применяются математические методы. Запись команд в системе MathCad на языке, очень близком к стандартному языку математических расчетов, упрощает постановку и решение задач.

И так, перечислим основные достоинства MathCad.

Во-первых, это универсальность пакета, который может быть использован для решения самых разнообразных инженерных, экономических, статистических и других научных задач.

Во-вторых, программирование на общепринятом математическом языке позволяет преодолеть языковой барьер между машиной и пользователем. Потенциальные пользователи пакета – от студентов до академиков.

И в-третьих, совместно применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ.

Но, к сожалению, популярный во всем мире пакет MathCad фирмы MathSoft, в России распространен еще слабо, как и все программные продукты подобно рода.

Видео:MathCAD Решение системы уравненийСкачать

Список использованных источников

1. Белинская, С. И. Использование пакета Mathcad в информатике : учебное пособие / С. И. Белинская. – Иркутск : ИрГУПС, 2012. – 84 с.

2. Гурский, Д. А. Вычисления в MATCHCAD 12 / Д. А. Гурский,
Е. С. Турбина. – СПб.: Питер, 2006. – 544 с.

3. Дьяконов, В. Mathcad 2000. Учебный курс / В. Дьяконов. – СПб.: Питер, 2001. – 592 с.

4. Макаров, Е. Г. Инженерные расчёты в MATCHCAD 14 /
Е. Г Макаров. – СПб.: Питер, 2007. – 592 с.

5. Охорзин, В. А. Прикладная математика в системе Mathcad /
В. А. Охорзин. – Лань, 2009. – 352 с.

6. Очков, В. Mathcad 14 для студентов, инженеров и конструкторов / В. Очков. – BHV.: – Спб, 2007. – 368 с.

7. Поршнев, С. В. Численные методы на базе MATCHCAD /
С. В. Поршнев, И. В. Беленкова. – СПб.: БХВ-Питербург, 2005. – 464 с.

8. Шушкевич, Г. Компьютерные технологии в математике. Система Mathcad 14. Часть 1 / Г. Шушкевич, С. Шушкевич. – Издательство Гревцова. 2010. – 288 с.

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Что такое given в mathcad

Видео:Математический анализ, 39 урок, Формулы и ряды Тейлора и МаклоренаСкачать

Решение уравнений

При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given — и имеющий следующую структуру:

Выражения с функцией Find()

Find(vl, v2, …, vn) — возвращает значение одной или ряда переменных для точного решения;

Знак равенства в уравнениях вызывается с математической панели БУЛЕВО(Boolean) или с клавиатуры клавишами «CTRL http://www.intuit.ru/2010/edi» >

Как и в предыдущем случае, сначала необходимо провести локализацию корней – задание начальной точки, от которой будет происходить поиск решения. Решение ищется методом итераций и при наличии нескольких корней, очевидно, будет найдено лишь ближайшее решение, если оно существует. Блок Given…Find(.) можно использовать и для решения уравнений одним неизвестным.

Пример 4.4

Решить систему уравнений 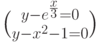>=0choose y-x^2-1=0>»>.

Осуществляется решение системы нелинейных уравнений при помощи блока Given…Find(.) (Рис.4.3).

• Локализация корней: задаем систему уравнений, строим график.
• По графику определяем три корня.
• Задаем последовательно разные начальные значения корней.

>»>

,

>-y=0″>

0.354 \ 1.125 end

,

>-y=0″>

-2.631 cdot 10^ \ 1 end

,

>-y1=0″>

17.015 \ 290.506 end

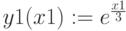
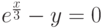
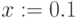
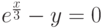
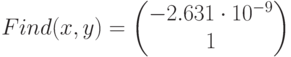
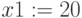
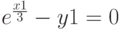
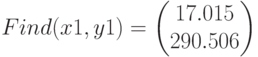
Поиск корней при помощи блока Given Minerr()

Функция Minerr использует тот же самый алгоритм, что и функция Find. Различие состоит в следующем. Функция Find ищет решение с заданной точностью и, если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, то она возвращает сообщение об ошибке. Функция Minerr возвращает это приближение. Системная переменная ERR дает величину ошибки.

Minerr (vl, v2, …, vn ) возвращает значения ряда переменных для приближенного решения.

Minerr() пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения. При использовании функции Minerr обязательно предусматривать проверку решений. Полезно как можно точнее указывать начальные приближения к решению.

Пример 4.5

Решить систему уравнений «>.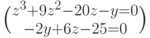

Решаем при помощи блока Given…Find(.) (Рис.4.4).

• Локализация корней: задаем систему уравнений, строим график.
• Графики имеют точку касания. Функция . Find( ) не решает систему.
• Функция Minerr() дает приближенное решение. Системная переменная ERR=0.37. Это ошибка определения корня. Проверка показывает максимальную ошибку 0.33.

,

Система не решается:

,

1.082 \ -9.169 end

,

Видео:MathCAD Решение системы линейных уравнений матричным методомСкачать

Решение уравнений с помощью функции Find(x)

Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:

— задать начальное приближение

— ввести служебное слово

• — записать уравнение, используя знак боулево равно
• — написать функцию find с неизвестной переменной в качестве параметра

В результате после знака равно выведется найденный корень.

Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.

В Mathcad можно писать программы двух видов

• 1)в виде скриптов(последовательность команд)
• 2)в виде настоящих программ с входными и выходными параметрами.

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).

Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).

Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Видео:Решение СЛАУ в пакете MathCadСкачать

Вычислительный блок Given/Odesolve

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:

• Given — ключевое слово;
• ОДУ и начальное условие, записанное с помощью логических операторов, причем начальное условие должно быть в форме у (t1) = b;
• odesoive(t, t1) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).

Допустимо, и даже часто предпочтительнее, задание функции Odesolve (t, t1, step) с тремя параметрами, где step— внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге — Купы, будет рассчитывать решение дифференциального уравнения. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск. Помните, что подбором этого параметра можно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Пример решения задачи Коши для ОДУ первого порядка у’ =у-у 2 посредством вычислительного блока приведен в листинге 11.1.

Листинг 11.1. Решение задачи Коши для ОДУ первого порядка

Не забывайте о том, что вставлять логические операторы следует при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры помните, что логическому знаку равенства соответствует сочетание клавиш + . Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано в листинге 11.1, так и в виде штриха, набрав его с помощью сочетания клавиш + (соответствующий пример будет приведен ниже в листинге 11.3.) Выбирайте тот или иной способ представления производной из соображений наглядности представления результатов — на ход расчетов он не влияет.

Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге-Кутты. Для смены метода необходимо нажатием правой кнопки мыши на области функции odesolve вызвать контекстное меню и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг) или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е. метод Рунге — Кутты с фиксированным шагом. Подробнее о различии этих методов сказано в разд. 11.3.

1. Электромагнитная волна (в религиозной терминологии релятивизма — «свет») имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например,

200 тыс км/с в стекле и

3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью «Температура эфира и красные смещения»), разную скорость для разных частот (см. статью «О скорости ЭМ-волн»)

2. В релятивизме «свет» есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский «свет» — это волнение ничего в ничем. У него нет среды-носителя колебаний.

3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.

4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те «подтверждающие теорию Эйнштейна факты», которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.

📽️ Видео

8. MathCad. Решение систем линейных алгебраических уравненийСкачать

Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать