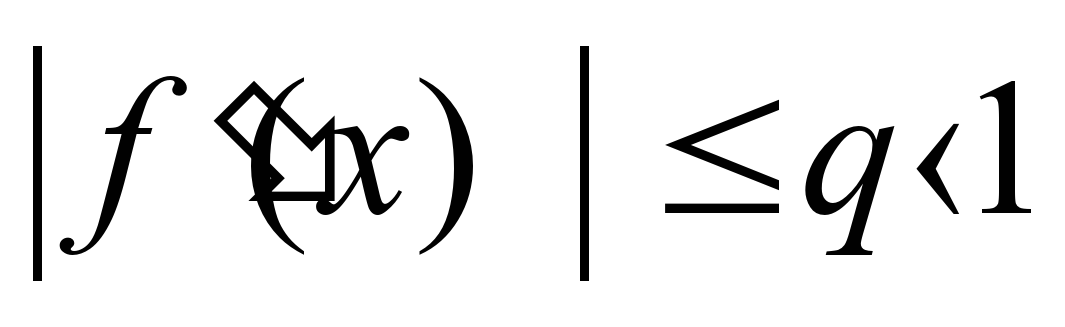Приближенное решение алгебраических и трансцендентных уравнений постановка задачи локализации корней

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение алгебраических и трансцендентных уравнений приближенными методами

Существуют формулы и правила для нахождения решений уравнений третей и четвертой степени, но эти формулы громоздкие и не удобные в применении, особенно в практических задачах. Если рассмотреть не алгебраические уравнения, то задача усложняется еще больше, потому что получить формулу для нахождения корней такого уравнения практически невозможно.

Трансцендентные уравнения – это уравнения в которых переменная x находится в нутрии тригонометрических функций, показательных, логарифмических функций.

Если записать уравнение в виде f(x)=0 , то известные алгоритмы обычно не накладывают не каких ограничений на конкретный вид функций f(x), чтобы найти корни такого уравнения, т. е. те значения x которые обращают уравнения тождества, необходимо подобрать численный метод этого решения, численный метод как правило дает приближенное значение.

Если имеется нелинейное уравнение , то в процессе приближенного отыскания обычно выделяют два этапа:

1. отделение корня;
2. уточнение корня.

Под отделение корня понимается определение промежутка содержащего один и только один корень. Вторая точка находится в зависимости от заданной точности и условия задачи, чаще всего процесс отделения корня уравнения не может быть алгоритмизирован, существуют только некоторые классы уравнений для которых разработаны специальные приемы позволяющие отделять корень. Эти приемы могут быть аналитические или графические.

Просмотр содержимого документа
«Решение алгебраических и трансцендентных уравнений приближенными методами »

ГБОУ СПО САМАРСКИЙ СОЦИАЛЬНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ

практического занятия №5-6

Решение алгебраических и трансцендентных уравнений приближенными методами

Автор-составитель: Родионова Т.В.

По дисциплине: «Численные методы»

Тип урока: практическое занятие

Тема. Решение алгебраических и трансцендентных уравнений приближенными методами.

Формировать умения решить алгебраические уравнения приближёнными методами.

Учить использовать логические приёмы активизации мыслительной деятельности.

Развивать алгоритмическое мышление.

Проверить уровень знаний некоторых методов приближённого решения уравнений.

Воспитывать вычислительную культуру, внимательность, аккуратность, дисциплинированность.

Развивать познавательный интерес, навыки самоконтроля, умения работать с тестом смешанного типа.

Оборудование: доска, планшеты функций, карточки с заданием (тест).

Орг. момент. (5 мин)

Целевая установка и актуализация знаний. (5 мин)

Решение уравнений(20 мин)

Самостоятельная работа студентов (тест). (10 мин)

Подведение итогов урока. Домашнее задание (5 мин)

Приветствие, проверка присутствующих. Сегодня на уроке мы рассмотрим пример применения метода итераций для решения алгебраических уравнений. Вспомним алгоритм решения и численные, приближённые методы решения уравнений. В конце урока выясним, как каждый знает основные положения темы с помощью мини-теста.

II. Актуализация знаний.

Что называется уравнением?

Что является корнем уравнения?

Какие уравнения называют трансцендентными, и какие — алгебраическими?

Что значит непрерывная функция, приведите пример?

Вспомним алгоритм решения алгебраических и трансцендентных уравнений. Из скольких этапов он состоит.

В каком случае говорят, что корень отделён?

Метод проб с десятичным делением

Метод проб с половинным делением

аким способом может быть отделён корень?

-Назовите методы уточнения корня.

-Чем похожи, и чем отличаются метод проб с десятичным делением и метод проб с половинным делением?

-Охарактеризуйте кратко остальные методы.

III. Решение уравнений.

1.На прошлом занятии мы рассмотрели теоретический блок метода итераций. Сейчас рассмотрим конкретный пример.

Пусть корень уравнения отделён и принадлежит интервалу [0,1; 0,2].

Для уточнения корня применим метод итераций. Представим уравнение в виде, удобном для применения метода

Проверим условия применимости метода. Найдем производную и сравним модуль её значения на заданном отрезке с1.

Пусть х = 0,15, тогда f ‘(0,15) =-0,005625

Получили |-0,005625| f ‘(х) | значит, метод итераций применить можно.

Примем за начальное приближение любое число из данного интервала.

х₀≈0,16 и будем вычислять последовательные приближения

Получили приближённое значение корня и ответ.

IV. Самостоятельная работа студентов (тест).

(см. Приложение 1.)

V. Подведение итогов урока. Домашнее задание.

1.Решить комбинированным методом проб и хорд с точностью до 0,001:

х 5 +0,2х-0,84=0, (положительный корень). (Отв.0,919)

2. Решить комбинированным методом хорд и касательных с точностью до 0,001:

х 6 +2х-1=0, (положительный корень). (Отв.0,493)

3.*Составить алгоритм и программу для нахождения приближенных решений алгебраических и (или) трансцендентных уравнений.

(см. Приложение 2.)

1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.

2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.

3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.

4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.

Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»

Вариант для преподавателя Вариант №1

Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.

Установите соответствие понятия определению:

1. Численные методы

2. Корень уравнения

3. Скорость сходимости

А) – это характеристика близости приближённого решения к точному решению при некоторых дополнительных ограничениях.

Б) позволяют получить численный ответ с помощью последовательности осуществимых численных операций.

В). – число, при подстановке которого в уравнение, получается верное равенство.

Установите соответствие уравнения его виду:

А) √х+3 + √3х-2 = 7; Б) lg х = 1 / х 2 ;

Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.

Среди предложенных функций выберите непрерывную:

А) у = 5х 4 -7х 2 +4х+10, Б) у = tg х,

В) у = 18 / х, Г) у = 5 / (х-1).

Решить уравнение х 4 -25х 2 +144=0

и выбрать правильный ответ.

Метод итераций можно применять для решения алгебраического уравнения, если:

Б) | f ‘(x)| 1 на отрезке [a,b];

Г) | f ‘(x)| 0 на отрезке [a,b].

Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.

Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то применяется формула………..

Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то

х₀ =b и применяется формула………..

Найти приближённое значение корня уравнения

х 3 +х 2 -3=0 на отрезке [1;1,5]., применяя метод хорд и метод касательных, с точностью до 0,01.

Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»

Вариант для преподавателя Вариант №2

Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.

Установите соответствие понятия определению:

1. Открытый интервал

2. Условие сходимости метода

3. Численные методы

А) — раздел математики, в котором разрабатываются численные методы решения задач.

Б) — это минимальные по возможности ограничения, при которых приближённое решение задачи стремится к точному решению.

В) – совокупность всех действительных чисел х , удовлетворяющих неравенству: а х b, где а и b – данные числа. Обозначается так (а,b).

Установите соответствие уравнения его виду:

А) sin 3 х = 2cosх; Б) 2х 2 -2х+1=0;

Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.

Среди предложенных функций выберите непрерывную:

А) у =, сtg х; Б) у = 3х 4 -5х 2 +2х+9;

В) у = 8 / х; Г) у = 15 / (х-2).

Решить уравнение х 4 — 13х 2 +36=0

и выбрать правильный ответ.

В процессе решения алгебраического уравнения отделение корня можно выполнить следующими способами:

А) практически; Б) аналитически;

В) графически; Г) на глаз.

Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.

Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то

х₀ =b и применяется формула………..

Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то применяется формула………..

Найти приближённое значение корня уравнения

х 3 -2х-1=0 на отрезке [1,5;2]., применяя метод десятичного деления и метод проб, с точностью до 0,01.

Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»

Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.

Установите соответствие понятия определению:

1. Численные методы

2. Корень уравнения

3. Скорость сходимости

А) – это характеристика близости приближённого решения к точному решению при некоторых дополнительных ограничениях.

Б) позволяют получить численный ответ с помощью последовательности осуществимых численных операций.

В). – число, при подстановке которого в уравнение, получается верное равенство.

Установите соответствие уравнения его виду:

А) √х+3 + √3х-2 = 7; Б) lg х = 1 / х 2 ;

Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.

Среди предложенных функций выберите непрерывную:

А) у = 5х 4 -7х 2 +4х+10, Б) у = tg х,

В) у = 18 / х, Г) у = 5 / (х-1).

Решить уравнение х 4 -25х 2 +144=0

и выбрать правильный ответ.

Метод итераций можно применять для решения алгебраического уравнения, если:

Б) | f ‘(x)| 1 на отрезке [a,b];

Г) | f ‘(x)| 0 на отрезке [a,b].

Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.

Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то применяется формула………..

Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то

х₀ =b и применяется формула………..

Найти приближённое значение корня уравнения

х 3 +х 2 -3=0 на отрезке [1;1,5]., применяя метод хорд и метод касательных, с точностью до 0,01.

Тест по теме «Численные методы решения алгебраических и трансцендентных уравнений»

Инструкция по выполнению заданий 1-2: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв.

Установите соответствие понятия определению:

1. Открытый интервал

2. Условие сходимости метода

3. Численные методы

А) — раздел математики, в котором разрабатываются численные методы решения задач.

Б) — это минимальные по возможности ограничения, при которых приближённое решение задачи стремится к точному решению.

В) – совокупность всех действительных чисел х , удовлетворяющих неравенству: а х b, где а и b – данные числа. Обозначается так (а,b).

Установите соответствие уравнения его виду:

А) sin 3 х = 2cosх; Б) 2х 2 -2х+1=0;

Инструкция по выполнению заданий № 3-5: выберите букву (буквы), соответствующую (щие) правильному варианту ответа, и запишите в колонку ответов.

Среди предложенных функций выберите непрерывную:

А) у =, сtg х; Б) у = 3х 4 -5х 2 +2х+9;

В) у = 8 / х; Г) у = 15 / (х-2).

Решить уравнение х 4 — 13х 2 +36=0

и выбрать правильный ответ.

В процессе решения алгебраического уравнения отделение корня можно выполнить следующими способами:

А) практически; Б) аналитически;

В) графически; Г) на глаз.

Инструкция по выполнению заданий № 6-8: в колонку ответов запишите формулу или число.

Для уточнения корня методом касательных, если f ‘(х) и f »(х) имеют одинаковые знаки на отрезке [а,b], то

х₀ =b и применяется формула………..

Для уточнения корня методом хорд, если f ‘(х) и f »(х) имеют разные знаки на отрезке [а,b], то применяется формула………..

Найти приближённое значение корня уравнения

х 3 -2х-1=0 на отрезке [1,5;2]., применяя метод десятичного деления и метод проб, с точностью до 0,01.

Практическая работа № 5

Приближенное решение алгебраического уравнения комбинированным методом

Содержание работы. Отыскание корня алгебраического уравнения комбинированным методом (методом проб и хорд или методом хорд и касательных).

Тип задания. Дано алгебраическое уравнение степени выше второй f(x)=0. Даются указания, какой именно корень требуется найти. Ставится задача отыскания приближенного значения корня с заданной точностью.

1. Графически отделить корень данного уравнения: найти отрезок [а; b] достаточно малой длины, внутри которого содержится искомый корень, и этот корень единственный.

Проверить аналитически, что:

Методом проб уточнить корень, добившись того, что длина отрезка [а; b] станет равной 0,1.

Избрать один из рекомендуемых комбинированных методов, составить расчетный бланк для записи вычислений.

Провести вычисления в соответствии с разработанной схемой.

Проверить полученный результат путем подстановки найденного корня в уравнение.

Задание 1. Вычислить наименьший положительный корень уравнения

2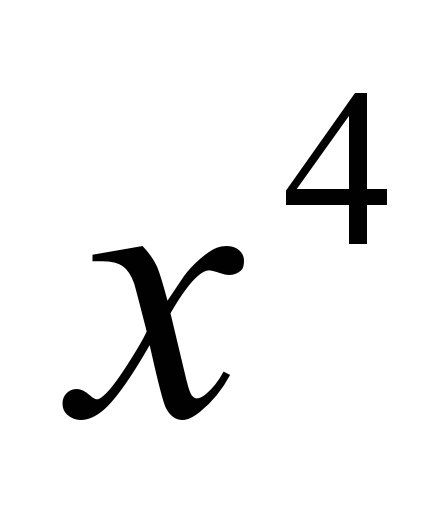— х – 2 = 0

комбинированным методом проб и хорд с точностью до четвертого десятичного знака.

Задание 2. Вычислить наименьший положительный корень уравнения

2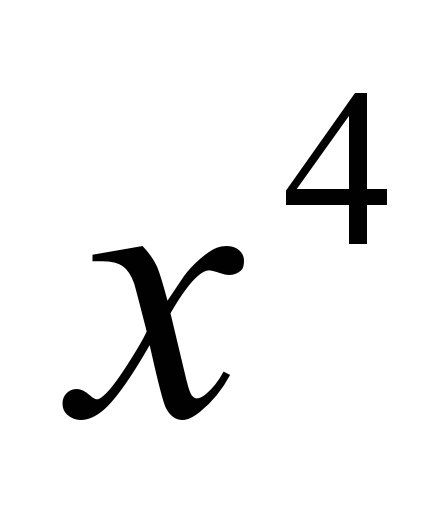— х – 2 = 0

комбинированным методом хорд и касательных.

1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.

2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.

3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.

4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.

Практическая работа №6*.

Приближенное решение трансцендентного уравнения

Тип задания. Найти корень данного уравнения F(x)=0 с заданной точностью одним из методов: 1) комбинированным методом проб и хорд;

2) комбинированным методом хорд и касательных;

3) методом итераций.

Если решено применить метод (1) или (2), то порядок выполнения работы тот, который изложен в работе № 5. Заметим лишь, что при выполнении данной работы следует пользоваться таблицами тех трансцендентных функций, которые содержат в уравнении (логарифм, тригонометрические функции и др.).

Приведем план выполнения данной работы в случае применения метода итераций.

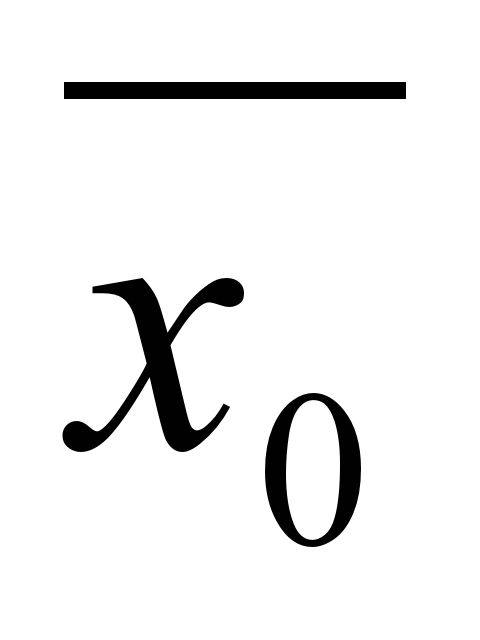
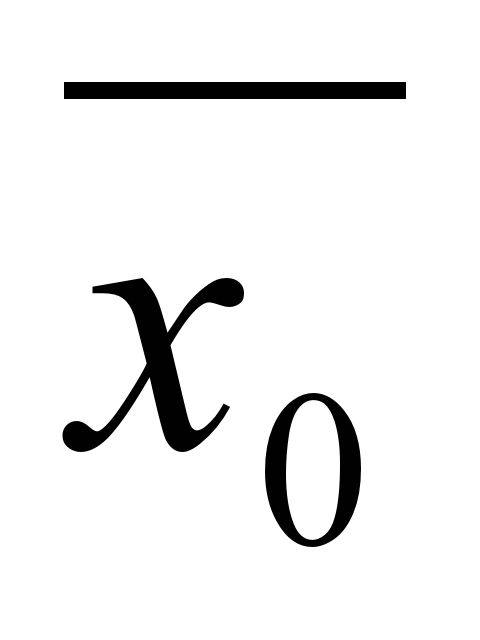
Графически или другим методом найти грубое приближенное значение корня . Отделить корень — найти отрезок [а; b] достаточно малой длины, в котором содержится корень (также находится в этом отрезке).

Привести данное уравнение F (х) = 0 к виду x = f (x). Из различных представлений уравнения в этом виде выбрать такое, при котором 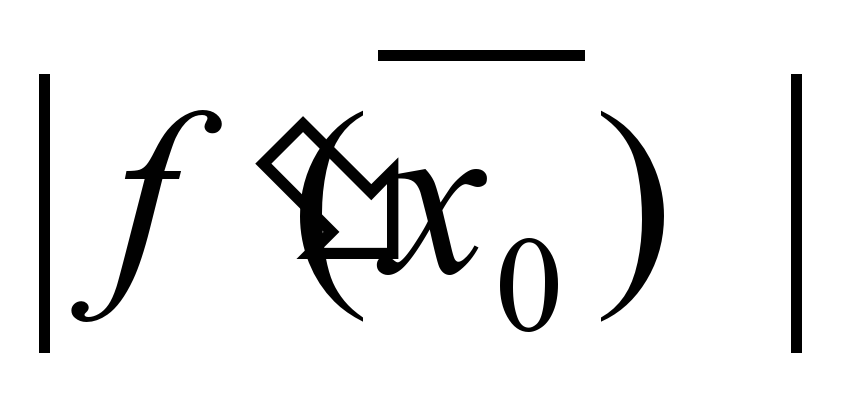есть малое число, значительно меньшее единицы (чем меньше, тем лучше).

Убедиться в том, что для всех х отрезка [а; b] выполняется неравенство

где q—малое число, значительно меньшее единицы. (Если 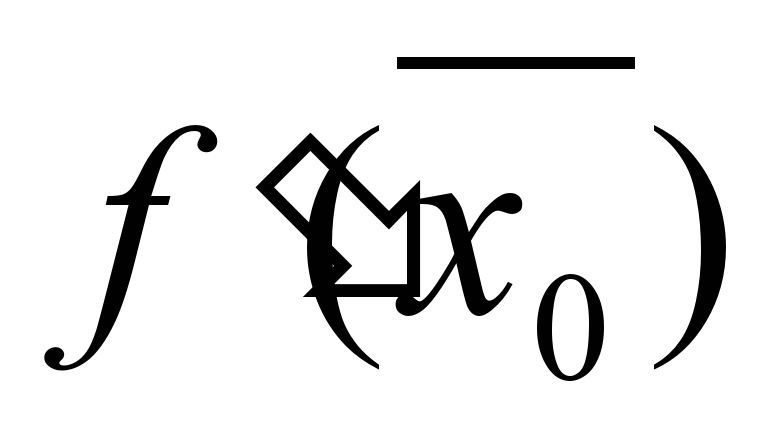) очень мало и длина отрезка [а; b] также очень мала, то эту проверку можно не выполнять.)

Составить расчетный бланк для вычисления последовательных приближений, приняв за начальное приближение 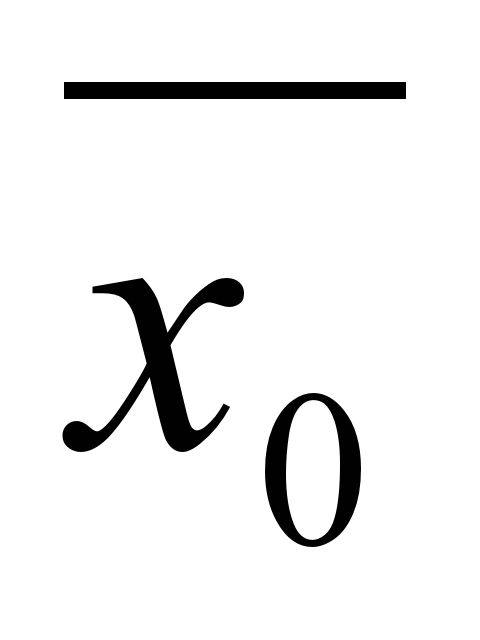или (если окажется удобным) любое другое число из отрезка [а; b]. (Обозначить начальное приближение х₀.) Провести вычисление последовательных приближений с одним запасным знаком. Вычисления прекратить, когда совпадут два соседних приближения в пределах заданной точности.

Если окажется необходимым, произвести дополнительную оценку точности найденного корня.

Задание. Вычислить корень уравнения lg x+5x—2=0 с точностью до 0,0001 методом итераций.

1. Костомаров Д.П. Программирование и численные методы – М.: Издательство МГУ, 2001.,стр.87-100.

2. Пирумов У.Г. Численные методы: Учебн. пособие для студентов – М.: Дрофа, 2004.,стр.23-41.

3. Костомаров Д.П. Вводные лекции по численным методам. М.: «Логос», МГУ,2004.,стр.53-70.

4. Пулькин С.П. Вычислительная математика. – М. «Просвещение», 1994., стр.84-123.

Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Раздел 2. Численные методы

1. Алгебраические и трансцендентные уравнения

2. Графический метод решения уравнений

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

( x )= g ( x ), (1)

где (х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения.

В общем случае нелинейное уравнение можно записать в виде:

где функция F ( x ) определена и непрерывна на конечном или бесконечном интервале .

? Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х: из этой совокупности называется корнем уравнения.

? Всякое число , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F ( )=0, называется корнем уравнения (1).

? Число называется корнем k -той кратности , если при x = вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:

F ( ) = F / ( ) = … = F ( k -1) ( ) = 0.

Однократный корень называется простым.

? Решить уравнение – значит найти множество всех корней этого уравнения.

Оно может быть конечным или бесконечным.

? Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные.

Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

где a ₀ , a ₁ , . , a_n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.

Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).

Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.

Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.

При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.

? Решить уравнение – это значит

· установить, имеет ли оно корни,

· и найти значение корней с заданной точностью.

? Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:

1. отделение корней , т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,

2. и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.

Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).

2. Графические методы решения уравнений

Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ) , где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Рисунок 1

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).

После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀, ординаты обоих графиков в этой точке равны между собой, т. е. f (х₀) = g (х₀). Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

Рисунок 2

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.

Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)

Рисунок 3 Рисунок 4

Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).

Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.

Перепишем уравнение следующим образом: lg х = Зх — 5.

Функции в левой и в правой части уравнения имеют общую область определения: интервал 0 . Поэтому будем искать корни именно в этом интервале.

Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x₁0,00001 и x₂1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x₁0,00001 и x₂1,75

Рисунок 5 Рисунок 6

Пример 3. Найти графически корни уравнения 2 х = 2х.

Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х₁ = 1 и х₂ = 2. Данное урав­нение имеет два корня х₁= 1 и х₂ = 2 (рис. 6).

Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0 , все корни которого лежат в промежутке [а, b ], следующую простую схему.

1. Представить указанное уравнение в виде (х) = g (х) с таким расчетом, чтобы функции у= (х) и у = g (х) были просты и удобны для исследования и построения.

2. На бумаге вычертить графики функций у = (х) и у = g (х) в промежутке [а, b ].

3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.

Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.

? Корень уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.

? Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.

Отделение корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.

Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.

Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.

1) Если непрерывная на отрезке функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке единственный.

Рассмотрим примеры поведения некоторых функций:

Рисунок 7

Для отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) , содержат не по одному корню.

Будем вычислять значения F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X ₁ и X ₂ (Концов выделенных отрезков).

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Численные методы решения алгебраических и трансцендентных уравнений в среде Microsoft Excel

Цель урока: Совершенствование умений и навыков по теме «Решение алгебраических и трансцендентных уравнений», применяя возможности MS Excel по решению алгебраических и трансцендентных уравнений. Отработать практическое освоение соответствующих умений и навыков.

Задачи урока:

• Образовательные – совершенствование умений студентов при решении алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel. Выработать умение применять теоретические знания в практических расчетах;
• Развивающие – познакомить студентов с применением компьютеров в качестве помощников при решении уравнений. Развивать у студентов математическую речь: создать ситуацию для применения основных понятий в речи; абстрактное мышление: создать ситуацию предъявления материала от общего к частному и от частного к общему, стимулировать самостоятельное обобщение материала сильными студентами;творческого мышления через создание условий для самореализации творческого потенциала обучающихся;
• Воспитательные – выработать у студентов умение рационально использовать время и возможности компьютерных технологий при решении задач. Воспитывать интерес к предмету через ситуацию успеха и взаимодоверия;ответственность перед самим собой.

Тип урока: комбинированный урок.

Вид урока: практическое занятие, продолжительность – 2 часа.

Оборудование урока:

• Компьютеры с OS MS Windows;
• Программа Microsoft Excel;
• Презентация по теме, выполненная в программе PowerPoint;
• Карточки с заданиями для самостоятельной работы.

Структура урока:

1.1. Мобилизующее начало, постановка целей и задач на урок;

1.2.Фронтальный опрос с целью выявления основных этапов решения задач с использованием ЭВМ;

1.3. Постановка задачи с целью повторения алгоритма решения уравнения f(x)=0 на отрезке [а;в] различными методами;

1.4.Подведение итогов 1 этапа урока.

2.Применение знаний, формирование умений и навыков:

2.1.Беседа с целью формулировки задания для самостоятельной работы и инструктажа по ее организации;

2.2.Самостоятельная работа в группах по выполнению задания различными методами решения алгебраических и трансцендентных уравнений в среде Microsoft Excel.

2.3.Подведение итога урока.

В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft PowerPoint.

ХОД УРОКА

1. Актуализация знаний

Мобилизующее начало, постановка целей и задач на урок.

На прошлых уроках мы с вами рассмотрели алгебраические и трансцендентные уравнения, выделили методы их решения и решали данные уравнения ручным счетом. А на сегодняшнем занятии мы будем совершенствовать умения и навыки при решении алгебраических и трансцендентных уравнений в среде Microsoft Excel.

Поэтому нам необходимо вспомнить и повторить знания, которые потребуются на этом уроке. В чем заключается процесс решения задачи с использованием ЭВМ?

В общем случае процесс решения задачи с использованием ЭВМ состоит из следующих этапов:

• 1.Постановка задачи и построение математической модели (этап моделирования);
• 2.Выбор метода и разработка алгоритма (этап алгоритмизации);
• 3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);
• 4.Отладка и использования программы на ЭВМ (этап реализации);
• 5.Анализ полученных результатов (этап интерпретации).

— В чем заключается постановка задачи?

— Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.

— В чем заключается общая постановка задачи?

— Общая постановка задачи. Найти действительные корни уравнения f(x) =0, где f(x) – алгебраическая или трансцендентная функция.

— Точные методы решения уравнений подходят только к узкому классу уравнений (квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические)

— В чем заключается задача численного нахождения корней уравнения?

— Задача численного нахождения корней уравнения состоит из двух этапов:

1. Отделение (локализация) корня;

2. Приближенное вычисление корня до заданной точности(уточнение корней)

— Какая задача называется уточнения корня?

-Уточнение корня. Если искомый корень уравнения f(x)=0, отделен, т.е. определен отрезок [a,b], на котором существует только один действительный корень уравнения, то далее необходимо найти приближенное значение коня с заданной точностью.

— Какими методами можно производить уточнения корня?

— Уточнения корня можно производить различными методами:

1) Метод половинного деления (бисекции);

2) Метод итераций;

3) Метод хорд (секущих);

4) Метод касательных (Ньютона);

5) Комбинированные методы.

— Объясните алгоритм решения уравнения f(x)=0 на отрезке [а;в] различными методами.

Применение знаний, формирование умений и навыков:

Видео:15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Практическое задание «Решение алгебраических и трансцендентных уравнений в среде Microsoft Excel»

• Ознакомиться с теоретической частью задания;
• Провести расчет для своего варианта индивидуального задания в Microsoft Excel
• Оформить презентацию в Ms PowerPoint, включающую:
  • постановку задачи;
  • алгоритм расчета;
  • таблицу с расчетом из Ms Excel, график исходной функции;
  • результат расчета и его анализ.

Индивидуальное расчетное задание

Дано: x 3 + 8x + 10 = 0

Найти: Отделить корень заданного уравнения, пользуясь графическим методом, и по методам вычислите один корень с точностью 0,001 при помощи программы на ПК

Графический метод: Для отделения корней уравнения естественно применять графический метод. График функции у = f (х) с учетом свойств функции дает много информации для определения числа корней уравнения f (х) = 0.

До настоящего времени графический метод предлага­лось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т.е. методы последовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью.

Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:

• если функция f(x) на концах отрезка [а,b] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз);
• повторим действия предыдущего пункта для полученного отрезка.

Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.

Задания для студентов первой группы

• Найдите приближенное значение уравнения заданного функцией x 3 + 8x + 10 = 0, с точностью е=0,001
• Представьте графически поставленную задачу в среде Microsoft Excel;

Метод половинного деления:Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.

Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.

Метод половинного деления или дихотомии (дихотомия — сопоставленность или противопоставленность двух частей целого). Метод основан на той идее, что корень лежит либо на середине интервала (a, b), либо справа от середины, либо — слева, что следует из существования единственного корня на интервале (a, b).

Алгоритм для программной реализации:

1. а:=левая граница b:= правая граница
2. m:= (a+b)/2 середина
3. определяем f(a) и f(m)
4. если f(a)*f(m) e повторяем, начиная с пункта 2
5. m — искомый корень.

Задания для студентов второй группы

1. Найдите приближенное значение уравнения заданного функцией x 3 + 8x + 10 = 0, с точностью е=0,001.
2. Расчет уравнения по методу половинного деления в среде Microsoft Excel.

Метод простой итерации: Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде ) и по формуле будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найти .

Подготовка:

1. Ищем числа m и M такие, что на (a, b);

2. Представляем , где ;

Алгоритм:

1. Выбираем х₀ из (a, b);

2. Вычисляем ;
3. Проверяем условие , где q=(M-m)/(M+m);

4. Если оно ложно, то переходим к пункту 7;

6. Переходим к пункту 2;

7. х₁ – искомый корень.

Задания для студентов третьей группы

1. Найдите приближенное значение уравнения заданного функцией x 3 + 8x + 10 = 0, с точностью е=0,001
2. Расчет уравнения по методу простой итерации в среде Microsoft Excel.

Метод хорд: Метод хорд заключается в замене кривой у = f(x) отрезком прямой, проходящей через точки (а, f(a)) и (b, f(b)). Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение.

Чтобы получить расчетную формулу метода хорд, за­пишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая у к нулю, найдем х:

,

Алгоритм метода хорд:

2) Вычислим следующий номер итерации: k = k + 1.

Найдем очередное k-e приближение по формуле: x_k = a — f(a)(b — a)/(f(b) — f(a)). Вычислим f(xk);

3) Если f(x_k)= 0 (корень найден), то переходим к п. 5.

4) Если |x_k – x_k–1| > ε, то переходим к п. 2;

5) Выводим значение корня x_k;

Задания для студентов четвертой группы

1. Найдите приближенное значение уравнения заданного функцией x 3 + 8x + 10 = 0, с точностью е=0,001.
2. Расчет уравнения по методу хорд в среде Microsoft Excel.
3. Метод касательных: В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных:

Теорема. Пусть на отрезке [а, b]выполняются условия:

1) функция f(x)и ее производные f'(х)и f»(x) непрерывны;

2) производные f'(x) и f»(x)отличны от нуля и сохраняют определенные постоянные знаки;

3) f(a)× f(b) 0, то итерационная последовательность сходится монотонно

Задания для студентов пятой группы

1. Найдите приближенное значение уравнения заданного функцией x 3 + 8x + 10 = 0, с точностью е=0,001.
2. Расчет уравнения по методу касательных в среде Microsoft Excel.

Студенты выполняют задания в группах и показывают полученное решение у доски (один представитель от группы), делают выводы о проделанной работе.

В данном уроке мы познакомились с решением алгебраических и трансцендентных уравнений в среде Microsoft Excel.

Уточнения корня производилось различными методами:

1) методом бисекции;

2) методом итераций;

3) методом секущих;

4) методом Ньютона;

1. Самый простейший из методов уточнения корня является метод половинного деления и используется во многих стандартных программных средствах.

2. Метод хорд в отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения. Он требует , чтобы один конец отрезка, на котором ищется корень был не подвижен. Берется один из концов отрезка. Метод является двухточечным, его сходимость монотонная и односторонняя. Метод хорд использует пропорциональное деление интервала.

3. В методе касательных в отличие от методов дихотомии и хорд задается не начальный интервал местонахождения корня, а его начальное приближение .

4. У метода хорд и у метода Ньютона имеется общий недостаток: на каждом шаге проверяется точность значения.

Видео:8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Математика : Приближённое решение алгебраических и трансцендентных уравнений

Приближённое решение алгебраических и трансцендентных уравнений

1. Общая постановка задачи. Найти действительные корни уравнения , где — алгебраическая или трансцендентная функция.

Точные методы решения уравнений подходят только к узкому классу уравнений (квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические).

В общем случае решение данного уравнения находится приближённо в следующей последовательности:

1) отделение (локализация) корня;

2) приближённое вычисление корня до заданной точности.

2. Отделение корня. Отделение действительного корня уравнения — это нахождение отрезка , в котором лежит только один корень данного уравнения. Такой отрезок называется отрезком изоляции (локализации) корня.

Наиболее удобным и наглядным является графический метод отделения корней:

1) строится график функции , и определяются абсциссы точек пересечения этого графика с осью , которые и являются корнями уравнения ;

2) если — сложная функция, то её надо представить в виде так, чтобы легко строились графики функций и . Так как , то . Тогда абсциссы точек пересечения этих графиков и будут корнями уравнения .

Пример.Графически отделить корень уравнения .

Решение. Представим левую часть уравнения в виде . Получим: Построим графики функций и .

Абсцисса точки пересечения графиков находится на отрезке , значит корень уравнения .

Если искомый корень уравнения отделён, т.е. определён отрезок , на котором существует только один действительный корень уравнения, то далее необходимо найти приближённое значение корня с заданной точностью.

Такая задача называется задачей уточнения корня.

Уточнение корня можно производить различными методами:

1) метод половинного деления (бисекции);

2) метод итераций;

3) метод хорд (секущих);

4) метод касательных (Ньютона);

5) комбинированные методы.

4. Метод половинного деления (бисекции).

Отрезок изоляции корня можно уменьшить путём деления его пополам.

Такой метод можно применять, если функция непрерывна на отрезке и на его концах принимает значения разных знаков, т.е. выполняется условие (1).

Разделим отрезок пополам точкой , которая будет приближённым значением корня .

Для уменьшения погрешности приближения корня уточняют отрезок изоляции корня. В этом случае продолжают делить отрезки, содержащие корень, пополам.

Из отрезков и выбирают тот, для которого выполняется неравенство (1).

В нашем случае это отрезок , где .

Далее повторяем операцию деления отрезка пополам, т.е. находим и так далее до тех пор, пока не будет достигнута заданная точность . Т.е. до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки или до выполнения неравенства .

Достоинство метода: простота (достаточно выполнения неравенства (1)).

Недостаток метода: медленная сходимость результата к заданной точности.

Пример. Решить уравнение методом половинного деления с точностью до 0,001.

Решение.Известен отрезок изоляции корня и заданная точность . По уравнению составим функцию .

Найдём значения функции на концах отрезка:

Проверим выполнение неравенства (1): — условие выполняется, значит можно применить метод половинного деления.

Найдём середину отрезка и вычислим значение функции в полученной точке:

Среди значений и выберем два значения разных знаков, но близких друг к другу. Это и . Следовательно, из отрезков и выбираем тот, на концах которого значения функции разных знаков. В нашем случае это отрезок и опять находим середину отрезка и вычисляем значение функции в этой точке:

, , , — заданная точность результата не достигнута, продолжим вычисления.

, — заданная точность результата достигнута, значит, нашли приближённое значение корня .

Ответ: корень уравнения с точностью до 0,001.

5. Метод хорд (секущих).

Этот метод применяется при решении уравнений вида , если корень уравнения отделён, т.е. и выполняются условия:

1) (функция принимает значения разных знаков на концах отрезка );

2) производная сохраняет знак на отрезке (функция либо возрастает, либо убывает на отрезке ).

Первое приближение корня находится по формуле: .

Для следующего приближения из отрезков и выбирается тот, на концах которого функция имеет значения разных знаков.

Тогда второе приближение вычисляется по формуле:

Вычисления продолжаются до тех пор, пока не перестанут изменяться те десятичные знаки, которые нужно оставить в ответе.

6. Метод касательных (Ньютона).

Этот метод применяется, если уравнение имеет корень , и выполняются условия:

1) (функция принимает значения разных знаков на концах отрезка );

2) производные и сохраняют знак на отрезке (т.е. функция либо возрастает, либо убывает на отрезке , сохраняя при этом направление выпуклости).

На отрезке выбирается такое число , при котором имеет тот же знак, что и , т. е. выполняется условие . Таким образом, выбирается точка с абсциссой , в которой касательная к кривой на отрезке пересекает ось . За точку сначала удобно выбирать один из концов отрезка.

Первое приближение корня определяется по формуле: .

Второе приближение корня определяется по формуле: .

Вычисления ведутся до совпадения десятичных знаков, которые необходимы в ответе, или при заданной точности — до выполнения неравенства .

Достоинства метода: простота, быстрота сходимости.

Недостатки метода: вычисление производной и трудность выбора начального положения.

7. Комбинированный метод хорд и касательных.

Если выполняются условия:

2) и сохраняют знак на отрезке ,

то приближения корня уравнения по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой — с избытком, то достаточно легко получить заданную степень точности корня.

Видео:Метод половинного деления. ДихотомияСкачать

Схема решения уравнения методом хорд и касательных

1. Вычислить значения функции и .

2. Проверить выполнение условия . Если условие не выполняется, то неправильно выбран отрезок .

3. Найти производные и .

4. Проверить постоянство знака производных на отрезке . Если нет постоянства знака, то неверно выбран отрезок .

5. Для метода касательных выбирается за тот из концов отрезка , в котором выполняется условие , т.е. и одного знака.

6. Приближения корней находятся:

а) по методу касательных: ,

б) по методу хорд: .

7. Вычисляется первое приближение корня: .

8. Проверяется выполнение условия: , где — заданная точность.

Если условие не выполняется, то нужно продолжить применение метода по схеме 1-8.

В этом случае отрезок изоляции корня сужается и имеет вид . Приближённые значения корня находятся по формулам:

Вычисления продолжаются до тех пор, пока не будет найдено такое значение , при котором и совпадут с точностью .

Пример. Решить уравнение методом хорд и касательных с точностью 0,001, если известно, что корень уравнения .

1. Вычислим значения функции на концах отрезка: , .

2. Проверим выполнение условия: — условие выполняется.

3. Найдём производные: и .

4. На отрезке производные и , т.е. сохраняют знак, следовательно, условие выполняется.

5. Выберем значение для метода касательных. Т.к. и , то .

6. Найдём приближения корня:

а) по методу касательных:

б) по методу хорд: .

7. Найдём первое приближение корня: .

8. Проверим выполнение условия: — условие не выполняется, значит нужно продолжить вычисления.

9. Отрезок изоляции корня имеет вид: .

10. Продолжим уточнение корня по схеме. Для этого найдём значения функции на концах суженного отрезка:

11. Проверим условие: — выполняется, значит можно продолжить применение метода.

12. Так как и на отрезке, то для метода касательных: .

13. Вычислим значение производной: .

14. Найдём новые значения концов отрезка изоляции:

15. Найдём второе приближение корня: .

16. Проверим выполнение условия: — неравенство неверное, значит необходимо продолжить вычисления.

17. Отрезок изоляции корня имеет вид: .

18. Вычислим значения функции:

19. Условие — выполняется.

20. Так как и на , то для метода касательных .

21. Вычислим производную: .

23. Найдём третье приближение корня: .

24. Проверим выполнение неравенства: — условие выполняется, значит, цель достигнута.

25. Следовательно, или — приближённое значение корня с точностью до 0,001.

📽️ Видео

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод итераций (последовательных приближений)Скачать

Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать

Численные методы - Занятие 1: Численное решение уравнения методом дихотомииСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Нелинейные уравненияСкачать

Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать

Численные методы. Часть 1Скачать

Метод простой итерации Пример РешенияСкачать

Алгебра 8 класс (Урок№20 - Нахождение приближённых значений квадратного корня.)Скачать

13 Шаговый метод Ручной счет Численные методы решения нелинейного уравненияСкачать

Приближенное вычисление квадратного корня. Алгебра, 8 классСкачать

Метод_Зейделя_ExcelСкачать