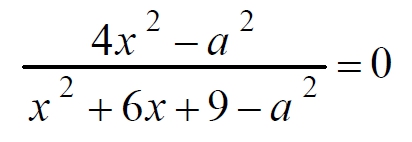Презентация к уроку
Загрузить презентацию (434 кБ)
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a, если a > 0, число – a, если a <
Неравенство | x | 0) равносильно двойному неравенству – a 0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a : | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 < | x + 3 < | x 0 | y > – 2 |
| – x – 3 – y – 2 = 4 | y = x + 9 |
| < | x + 3 < | x 2 – 1) х = а + 1. Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи: 1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения 2) а = – 1; получаем ОX = О , и очевидно х – любое. Ответ:
3. Решения примеров (из вариантов С) 1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня. Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 | Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
Числовая прямая при этом разбивает на 5 промежутков
Для случая 3) х0 = – b | 2a = 2, y0 = 25 : 2 + 25 – 10 = 2,5 Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10. Построим график функции, заданной равенством
Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 2 – | x | = 6 1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10 1. Решить уравнение | x – 5 | – | 2x + 3| = 10 5. Итог урока 1. Определение модуля. 6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012 Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать  Линейные уравнения с параметромРассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где (p(a)) и (q(a))- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все (x) при всех значениях параметра (a). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение: (x=frac ) при (p(a)≠0.) Если же (p(a)=0) и (q(a)=0), то решением данного уравнения является любое число. И последний случай, когда (p(a)=0),а (q(a)≠0), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с (x) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров: Решить уравнение (ax-5a=7x-3) при всех возможных (a). Перенесем все одночлены с (x) влево, а оставшиеся члены – вправо. И вынесем (x) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда ((a-7)≠0). Тогда мы можем поделить все уравнение на (a-7) и выразить: $$x=frac.$$ Второй случай, когда ((a-7)=0), получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра (а). Например, (x=frac) при (a=0,) (x=frac) при (a=1) и т.д. Найдите все (a), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число. Раскроем скобки и перенесем все члены, содержащие (x), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку (x) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: ((a-1)=0),т.е. (a=1) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число. Из ОДЗ видно, что (5a+x≠0) и (x-5a≠0,) таким образом, (x≠±5a.) Приведем уравнение к общему знаменателю (x^2-25a^2) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$ После преобразований получили линейное уравнение. Первый случай: (a=0.) Получаем уравнение (0*x=0.) Решениями этого уравнения будет любое число, кроме (x=0) (ОДЗ (x≠±5a)). Ответ: При (a=0) решениями уравнения будут все действительные числа, кроме (x=0.) Если (a≠0,) то решений нет. Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать  Задача 37757 При каких значениях параметра а.Условие
При каких значениях параметра а уравнение (x^(2)-6x-a)/(2x^(2)-ax-a^(2)) =0 имеет ровно два различных решения. Решение
Дробь равна 0 если числитель равен 0, а знаменатель отличен от 0. Квадратное уравнение имеет два корня, если дискриминант положителен. Значит решение неравенства: Из этого множества надо исключить те значения параметра а, при которых корни числителя являются корнями и знаменателя. Корни знаменателя: Видео:Уравнения с параметром. Алгебра, 8 классСкачать  Решение №673 Найдите все значения a, при каждом из которых уравнение (4x^2-a^2)/(x^2+6x+9-a^2)=0 имеет ровно два различных корня.Найдите все значения a, при каждом из которых уравнение имеет ровно два различных корня.
Есть три секунды времени? Для меня важно твоё мнение! Насколько понятно решение? Средняя оценка: 5 / 5. Количество оценок: 2 Оценок пока нет. Поставь оценку первым. Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️ Вступай в группу vk.com 😉 Расскажи, что не так? Я исправлю в ближайшее время В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил. 🔥 ВидеоПараметры с нуля до уровня ЕГЭ. Линейные уравнения. Математик МГУСкачать  ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать  Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать  9 класс, 7 урок, Задачи с параметрамиСкачать  Задача 17 ЕГЭ профильный. Параметры с нуляСкачать  Найдите все значения параметра m≦100 , при которых уравнение σ(x)=m имеет решениеСкачать  Математика При каждом значении параметра к решите уравнение х^2 - (2к - 2)х – 4к = 0Скачать  ✓ Новые четыре способа решить параметр | ЕГЭ. Задание 17. Математика. Профиль | Борис ТрушинСкачать  При каких значениях параметра уравнение имеет единственный кореньСкачать  Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Аналитический методСкачать  Решаем неравенство с параметром. ЕГЭ №18 | Математика TutorOnlineСкачать  9 класс. Алгебра. Уравнения с параметромСкачать  УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать  Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать  Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать  Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  Сможешь решить уравнение с параметром? Стандартное-нестандартное уравнениеСкачать  |
