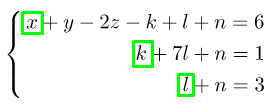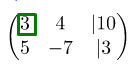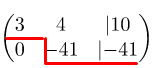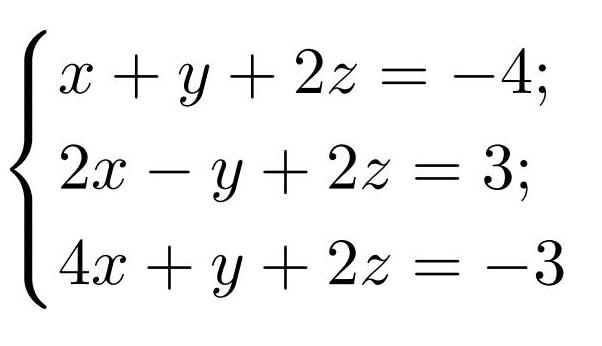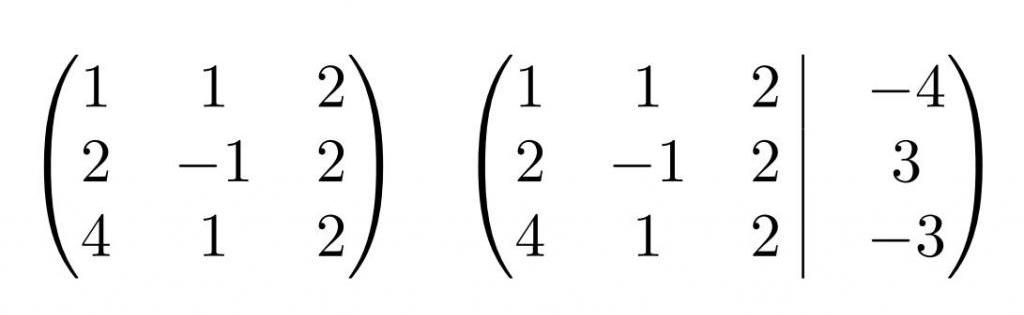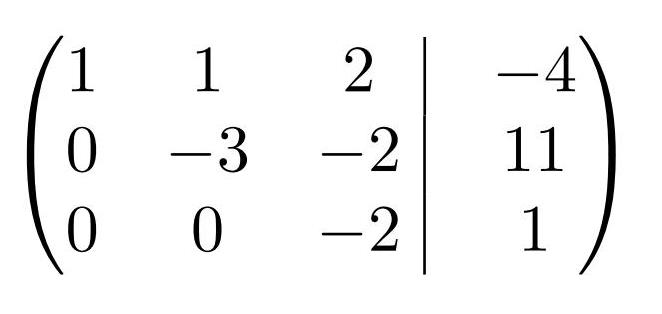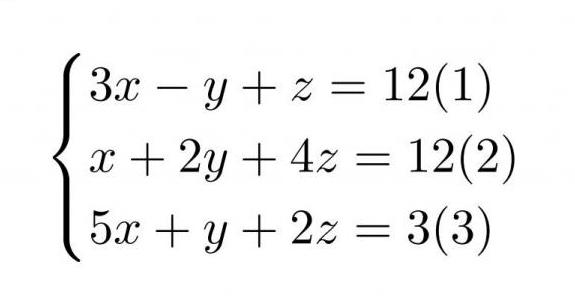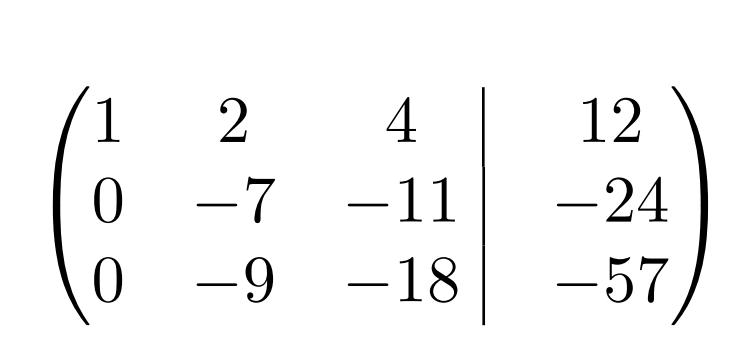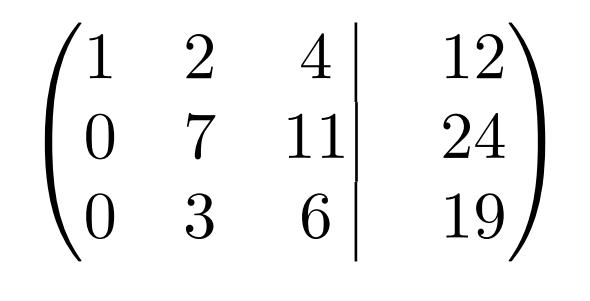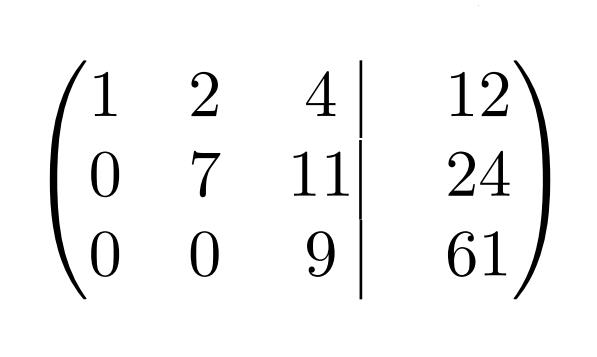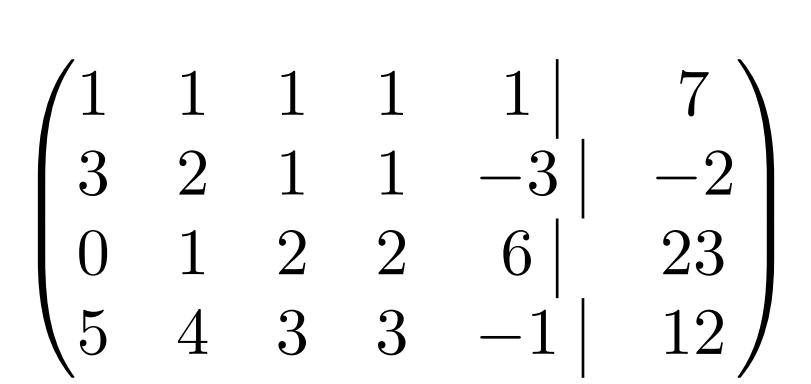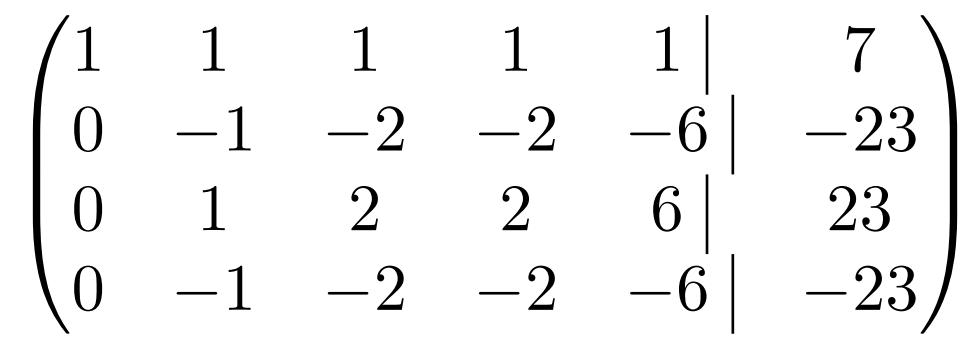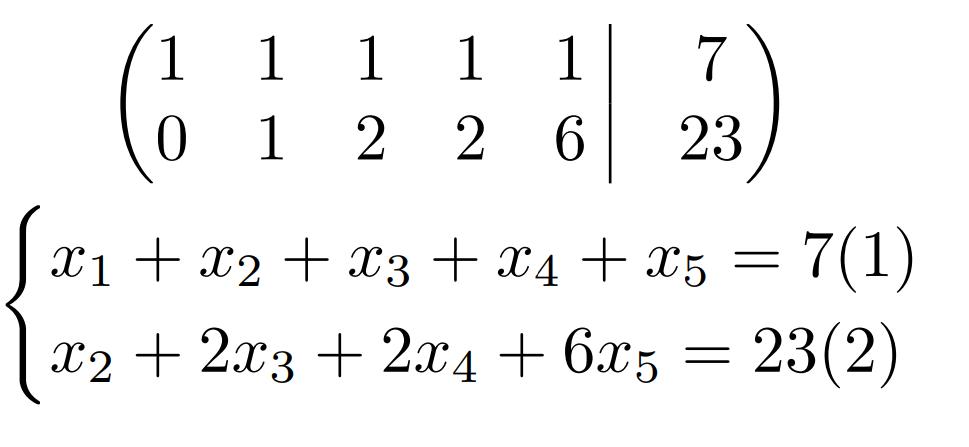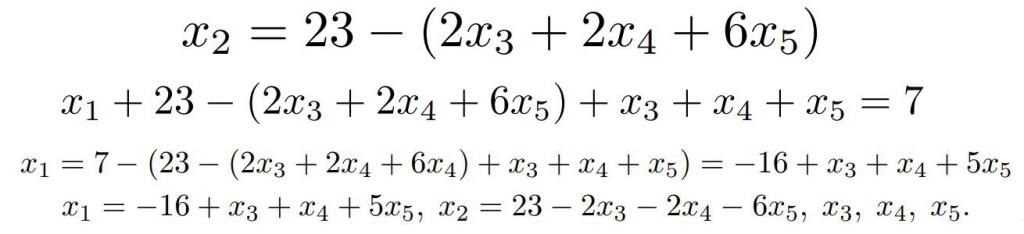Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
- Понятие метода Гаусса
- Преимущества метода:
- Элементарные преобразования системы линейных уравнений
- Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы
- Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
- Решение методом Гаусса прикладных задач на примере задачи на сплавы
- Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений
- Метод Гаусса и системы линейных уравнений, не имеющие решений
- Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
- Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений
- Метод Гаусса и системы, в которых число неизвестных больше числа уравнений
- Метод Гаусса – теорема, примеры решений
- Определения и обозначения
- Простейшие преобразования элементов матрицы
- Алгоритм решения методом Гаусса пошагово
- Шаг 1. Переписываем систему в виде матрицы
- Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю
- Шаг 3. Приводим матрицу к ступенчатому виду
- Шаг 4. Записываем эквивалентную систему
- Шаг 5. Производим проверку (решение системы обратным путём)
- Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений
- Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений
- Примеры решения методом Гаусса
- Заключение
- Метод Гаусса для чайников: примеры решений
- Что значит решить методом Гаусса?
- Матрицы, их свойства
- Определитель
- Классификация систем
- Элементарные преобразования
- Прибавление строки, умноженной на коэффициент
- В общем виде
- Когда нет решений
- Когда решений бесконечное количество
- Решение на конкретных примерах
- Пример неопределенной системы
- Пример несовместной системы
- Преимущества и недостатки метода
- Применение
Видео:Решение системы уравнений методом ГауссаСкачать

Понятие метода Гаусса
Чтобы сразу же понять суть метода Гаусса, остановите ненадолго взгляд на анимации ниже. Почему одни буквы постепенно исчезают, другие окрашиваются в зелёный цвет, то есть становятся известными, а числа сменяются другими числами? Подсказка: из последнего уравнения совершенно точно известно, чему равна переменная z .
Догадались? В такой системе, называемой трапециевидной, последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса, далее — просто обратный ход), из которого находят предыдущую переменную, и так далее.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее — просто прямой ход). Пример такой системы и её решения как раз и был приведён на анимации в начале урока.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение — переменной x .
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
У студентов наибольшие трудности вызывает именно прямой ход, то есть приведение исходной системы к трапециевидной. И это несмотря на то, что преобразования, которые необходимы для этого, называются элементарными. И называются неслучайно: в них требуется производить умножение (деление), сложение (вычитание) и перемену уравнений местами.
Преимущества метода:
- при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;
- методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
- можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
- метод основан на элементарных (школьных) методах — методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.
Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:
Теперь нам известны значения уже двух переменных — z и y. Подставляем их в первое уравнение и получаем значение переменной x:
Из предыдущих шагов выписываем решение системы уравнений:
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Элементарные преобразования системы линейных уравнений
Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение — один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.
На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.
При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:
- переставлять местами строки (это и было упомянуто в самом начале этой статьи);
- если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
- удалять «нулевые» строки, где все коэффициенты равны нулю;
- любую строку умножать или делить на некоторое число;
- к любой строке прибавлять другую строку, умноженное на некоторое число.
В результате преобразований получаем систему линейных уравнений, эквивалентную данной.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы
Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы — квадратная, то есть в ней число строк равно числу столбцов.
Пример 2. Решить методом Гаусса систему линейных уравнений
Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.
Для упрощения внешнего вида решения составим расширенную матрицу системы:
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты — свободные члены.
Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на 



Это возможно, так как
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:
Для упрощения второй строки полученной системы умножим её на 
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на 

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.
Решение найдём «с конца» — обратный ход. Для этого из последнего уравнения определим z: 
Подставив это значение в предшествующее уравнение, найдём y:
Из первого уравнения найдём x:
Ответ: решение данной системы уравнений — 
Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.
Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
Пример 3. Решить систему линейных уравнений:
Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма — здесь уже четыре уравнения и четыре неизвестных.
Пример 4. Решить систему линейных уравнений методом Гаусса:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 



Теперь нужно с помощью второго уравнения исключить переменную 
Проведём теперь собственно исключение переменной 


Теперь с помощью третьего уравнения исключим переменную 

Получили систему уравнений, которой эквивалентна заданная система:
Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной «икс четвёртое»:

Это значение подставляем в третье уравнение системы и получаем

откуда находим «икс третье»:

Далее, подставляем значения 



Наконец, подстановка значений


откуда находим «икс первое»:

Ответ: данная система уравнений имеет единственное решение 
Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение.
Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Решение методом Гаусса прикладных задач на примере задачи на сплавы
Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач — на сплавы. Аналогичные задачи — задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.
Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй — 30%, третий — 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение. Составляем систему линейных уравнений:
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:
Составляем расширенную матрицу системы:
Внимание, прямой ход. Путём сложения (в нашем случае — вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:
Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.
Применяем обратный ход. Находим решение с конца. Видим, что 
Из второго уравнения находим

Из третьего уравнения —

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан то же ответ, если система имеет однозначное решение.
О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение «Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным» — своего рода краткая инструкция по совершению открытий.
Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот — неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.
С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений
Следующий пример — совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.
После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

соответствующие уравнению вида
Если во всех уравнениях имеющих вид
свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.
Пример 6. Решить методом Гаусса систему линейных уравнений:
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную 

Теперь вторую строку прибавим к третьей и четвёртой.
В результате приходим к системе
Последние два уравнения превратились в уравнения вида 
Чтобы удовлетворить второму уравнению, мы можем для 






Как заданная, так и последняя системы совместны, но неопределённы, и формулы
при произвольных 

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Метод Гаусса и системы линейных уравнений, не имеющие решений
Следующий пример — несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.
Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. 
Пример 7. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 



Теперь нужно с помощью второго уравнения исключить переменную 
Для исключения 


Теперь с помощью третьего уравнения исключим переменную 

Заданная система эквивалентна, таким образом, следующей:
Полученная система несовместна, так как её последнее уравнение 
Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
Пример 8. Решить систему линейных уравнений:
Видео:Лекция 14. Метод Гаусса.Скачать

Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений
Следующий пример — система линейных уравнений, в которой число неизвестных меньше числа уравнений.
Пример 9. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 




Теперь нужно с помощью второго уравнения исключить переменную 

Проведём теперь исключение переменной 


Четвёртая и третья строки — одинаковые, поэтому четвёртую исключаем из матрицы. А третью умножаем на 
Получили следующую систему уравнений, которой эквивалентна заданная система:




Ответ: данная система уравнений имеет единственное решение (1; 1; 1).
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса и системы, в которых число неизвестных больше числа уравнений
Следующий пример — система линейных уравнений, в которой число неизвестных больше числа уравнений.
Если при выполнении преобразований в расширенной матрице системы встретилось хотя бы одно уравнение вида

с равным нулю свободным членом, то в итоге получим эквивалентную исходной системе систему линейных уравнений, в которой число уравнений меньше числа переменных, а уравнения вида (*) удовлетворяются при любых значениях неизвестных. Их можно отбросить.
Неизвестным, которые удовлетворяли уравнению вида 0 = 0, например, третьему и четвёртому (*, отброшенным уравнениям), придадим произвольные значения (пример 2). Они чаще всего записываются так: 


Пример 10. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. Далее ко второй строке прибавляем первую, умноженную на 
Заданная система эквивалентна, таким образом, следующей:
В ней отсутствуют уравнения, дающие однозначные значения для 







Как заданная, так и последняя системы совместны, но неопределённы, и формулы
при произвольных 

Видео:Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Метод Гаусса – теорема, примеры решений
Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.
Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ
Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.
Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.
У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.
Видео:решение системы уравнений методом ГауссаСкачать

Определения и обозначения
Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.
Для начала систематизируем знания о системах линейных уравнений.
СЛАУ в зависимости от её элементов может иметь:
- Одно решение;
- много решений;
- совсем не иметь решений.
В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.
Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:
- перемена мест уравнений системы;
- почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
- сложение к обеим частям одного из уравнений определённых частей другого уравнения.
Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.
Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:
где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.
Если =
=
=
, тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.
Множественные числа ,
,
называются решением СЛАУ, если при подстановке
,
,
в СЛАУ получим числовые тождества.
Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:
– это основная матрица СЛАУ.
– матрица столбец неизвестных переменных.
– матрица столбец свободных членов.
Если к основной матрице добавить в качестве
– ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой
, а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:
Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.
Если с системой уравнений:
Произвести такие действия:
- умножать обе части любого из уравнений на произвольное и отличное от нуля число
;
- менять местами уравнения;
- к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число
,
тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.
Теперь можно перейти непосредственно к методу Гаусса.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Видео:14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать

Простейшие преобразования элементов матрицы
Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:
Из уравнения запишем расширенную матрицу:
Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.
На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:
1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:
.
2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).
3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.
4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.
5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:
Для удобства умножаем первую строку на (-3):
Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:
В итоге получилось такое преобразование:
Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:
В матрице верхняя строка преобразовалась:
Первую строку делим на и преобразовалась нижняя строка:
И верхнюю строку поделили на то же самое число :
Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.
Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:
.
Видео:МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Алгоритм решения методом Гаусса пошагово
После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:
Шаг 1. Переписываем систему в виде матрицы
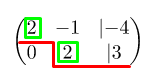
Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю
Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на
.
Шаг 3. Приводим матрицу к ступенчатому виду
Теперь вторую строку можно поделить на 2 и получается:
Верхнюю строку делим на и приводим матрицу к ступенчатому виду:
Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.
Шаг 4. Записываем эквивалентную систему
После наших элементарных преобразований получилась эквивалентная система:
Шаг 5. Производим проверку (решение системы обратным путём)
Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:
находим :
,
,
.
После находим
:
,
.
.
Как видим, уравнение решено правильно, так как ответы в системе совпадают.
Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений
Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.
Дана система уравнений:
Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.
Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную
:
Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим
. И последнее, находим первое уравнение
.
Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.
Когда выражается через
и
в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:
- берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на
,
- берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на
.
И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:
Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:
В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно
, чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.
Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.
В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.
Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.
Видео:Как решить систему уравнений методом Гаусса? Просто с лидеромСкачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений
Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.
Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.
В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:
1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.
Например, вам попалась подобная система:
У нас получается такая ситуация
Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.
Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.
2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где
– число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло
вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:
Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:
В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных
,
и
, и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.
3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной
. Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной
. Если же
уже исключались, тогда переходим к
,
и т. д.
Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :
Такая система уравнений после преобразования выглядит так:
Вы наверное уже обратили внимание, что вместе с исключились
и
. Поэтому решение методом Гаусса продолжаем исключением переменной
из всех уравнений системы, а начнём мы с третьего уравнения:
Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:
Допусти, что система уравнений стала:
В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:
В нашем примере это ,
и
. В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:
Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: ,
,
, где
,
,
– произвольные числа.
Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.
В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении:
, а из первого уравнения получаем:
=
=
В итоге, получился результат, который можно и записать.
Ответ
,
,
,
,
,
.
Видео:6 способов в одном видеоСкачать

Примеры решения методом Гаусса
Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.
Задача
Решить систему линейных алгебраических уравнений методом Гаусса:
Решение
Выписываем матрицу, куда добавляем столбец свободных членов:
Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:
Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой
превратился в
. Для этого можно ко второй строке прибавить первую строку и умножить на
.Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на
(разрешающий элемент данного шага).
Соответственно, первая строка остаётся неизменной, а вторая поменяется:
Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на
и только после этого ко второй строке прибавить изменённую после умножения на
вторую строку. Вот что получилось:
. Теперь прибавляем со второй строки
первую строку
. У нас получился
, который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:
Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.
Итак, у нас получился ступенчатый вид матрицы:
Записываем новую систему уравнений:
Для проверки решаем систему обратным ходом. Для этого находим сначала :
Так как найден, находим
:
.
Подставляем в изначальную нашу систему уравнений найденные и
:
и
.
Как видите из решения, система уравнений решена верно. Запишем ответ.
Ответ
Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.
Задача
Решить систему уравнений методом Гаусса:
Решение
Составляем матрицу, куда вписываем и свободные члены:
Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку:
. В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем
, и
. Аналогично,
и
. И умножаем свободный член
. Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:
Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:
Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:
В результате получилась ступенчатая система уравнений:
Сначала находим :
,
.
Обратный ход:
Итак, уравнение системы решено верно.
Ответ
,
,
.
Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.
Задача
Решите систему уравнений методом Гаусса:
Решение
В уравнении , то есть
– ведущий член и пусть
≠ 0
Из данного уравнения составим расширенную матрицу:
Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: ,
,
. Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную
из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в
теперь стоит 0.
Поменяем вторую и третью строку местами и получим:
Получилось так, что =
b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную
из третьей и четвёртой строк:
Получилась такая матрица:
Также, учитывая, что =
, умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную
и получаем новую систему уравнений:
Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,
из третьего: =
=
=
второе уравнение находим: =
=
= 2,
из первого уравнения: =
.
Значит, решение системы такое: (1, 2, -1, -2).
Ответ
,
,
,
.
Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.
Задача
Решить систему уравнений методом Гаусса:
Решение
Записываем расширенную матрицу системы:
Сначала смотрим на левое верхнее число:
Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:
Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:
Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:
Получился ступенчатый вид уравнения:
,
,
,
,
.
.
Ответ
,
,
.
Видео:Метод Гаусса решения систем линейных уравненийСкачать

Заключение
Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.
Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.
Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.
Литература для общего развития:
Видео:Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Метод Гаусса для чайников: примеры решений



В данной статье метод рассматривается как способ решения систем линейных уравнений (СЛАУ). Метод является аналитическим, то есть позволяет написать алгоритм решения в общем виде, а потом уже подставлять туда значения из конкретных примеров. В отличие от матричного метода или формул Крамера, при решении системы линейных уравнений методом Гаусса можно работать и с теми, что имеют решений бесконечно много. Или не имеют его вовсе.
Видео:Метод Гаусса Пример РешенияСкачать

Что значит решить методом Гаусса?
Для начала необходимо нашу систему уравнений записать в виде матрицы. Выглядит это следующим образом. Берется система:
Коэффициенты записываются в виде таблицы, а справа отдельным столбиком — свободные члены. Столбец со свободными членами отделяется для удобства вертикальной чертой. Матрица, включающая в себя этот столбец, называется расширенной.
Далее основную матрицу с коэффициентами нужно привести к верхней треугольной форме. Это основной момент решения системы методом Гаусса. Проще говоря, после определенных манипуляций матрица должна выглядеть так, чтобы в ее левой нижней части стояли одни нули:
Тогда, если записать новую матрицу опять как систему уравнений, можно заметить, что в последней строке уже содержится значение одного из корней, которое затем подставляется в уравнение выше, находится еще один корень, и так далее.
Это описание решения методом Гаусса в самых общих чертах. А что получится, если вдруг у системы нет решения? Или их бесконечно много? Чтобы ответить на эти и еще множество вопросов, необходимо рассмотреть отдельно все элементы, использующиеся при решении методом Гаусса.
Видео:12. Решение систем линейных уравнений методом ГауссаСкачать

Матрицы, их свойства
Никакого скрытого смысла в матрице нет. Это просто удобный способ записи данных для последующих операций с ними. Бояться их не надо даже школьникам.
Матрица всегда прямоугольная, потому что так удобнее. Даже в методе Гаусса, где все сводится к построению матрицы треугольного вида, в записи фигурирует прямоугольник, только с нулями на том месте, где нет чисел. Нули можно не записывать, но они подразумеваются.
Матрица имеет размер. Ее «ширина» — число строк (m), «длина» — число столбцов (n). Тогда размер матрицы A (для их обозначения обычно используются заглавные латинские буквы) будет обозначаться как Am×n. Если m=n, то эта матрица квадратная, и m=n — ее порядок. Соответственно, любой элемент матрицы A можно обозначить через номер его строки и столбца: axy; x — номер строки, изменяется [1, m], y — номер столбца, изменяется [1, n].
В методе Гаусса матрицы — это не основной момент решения. В принципе, все операции можно выполнять непосредственно с самими уравнениями, однако запись получится куда более громоздкая, и в ней будет гораздо легче запутаться.
Видео:Универсальный алгоритм решения систем по методу ГауссаСкачать

Определитель
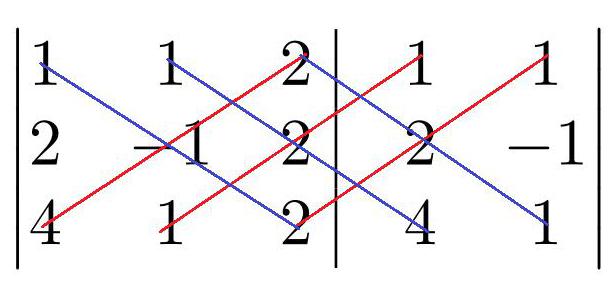
Еще у матрицы есть определитель. Это очень важная характеристика. Выяснять его смысл сейчас не стоит, можно просто показать, как он вычисляется, а потом рассказать, какие свойства матрицы он определяет. Наиболее простой способ нахождения определителя — через диагонали. В матрице проводятся воображаемые диагонали; элементы, находящиеся на каждой из них, перемножаются, а затем полученные произведения складываются: диагонали с наклоном вправо — со знаком «плюс», с наклоном влево — со знаком «минус».
Крайне важно отметить, что вычислять определитель можно только у квадратной матрицы. Для прямоугольной матрицы можно сделать следующее: из количества строк и количества столбцов выбрать наименьшее (пусть это будет k), а затем в матрице произвольным образом отметить k столбцов и k строк. Элементы, находящиеся на пересечении выбранных столбцов и строк, составят новую квадратную матрицу. Если определитель такой матрицы будет числом, отличным от нуля, то назовется базисным минором первоначальной прямоугольной матрицы.
Перед тем как приступить к решению системы уравнений методом Гаусса, не мешает посчитать определитель. Если он окажется нулевым, то сразу можно говорить, что у матрицы количество решений либо бесконечно, либо их вообще нет. В таком печальном случае надо идти дальше и узнавать про ранг матрицы.
Классификация систем
Существует такое понятие, как ранг матрицы. Это максимальный порядок ее определителя, отличного от нуля (если вспомнить про базисный минор, можно сказать, что ранг матрицы — порядок базисного минора).
По тому, как обстоят дела с рангом, СЛАУ можно разделить на:
- Совместные. У совместных систем ранг основной матрицы (состоящей только из коэффициентов) совпадает с рангом расширенной (со столбцом свободных членов). Такие системы имеют решение, но необязательно одно, поэтому дополнительно совместные системы делят на:
- — определенные — имеющие единственное решение. В определенных системах равны ранг матрицы и количество неизвестных (или число столбцов, что есть одно и то же);
- — неопределенные — с бесконечным количеством решений. Ранг матриц у таких систем меньше количества неизвестных.
- Несовместные. У таких систем ранги основной и расширенной матриц не совпадают. Несовместные системы решения не имеют.
Метод Гаусса хорош тем, что позволяет в ходе решения получить либо однозначное доказательство несовместности системы (без вычисления определителей больших матриц), либо решение в общем виде для системы с бесконечным числом решений.
Элементарные преобразования
До того как приступить непосредственно к решению системы, можно сделать ее менее громоздкой и более удобной для вычислений. Это достигается за счет элементарных преобразований — таких, что их выполнение никак не меняет конечный ответ. Следует отметить, что некоторые из приведенных элементарных преобразований действительны только для матриц, исходниками которых послужили именно СЛАУ. Вот список этих преобразований:
- Перестановка строк. Очевидно, что если в записи системы поменять порядок уравнений, то на решение это никак не повлияет. Следовательно, в матрице этой системы также можно менять местами строки, не забывая, конечно, про столбец свободных членов.
- Умножение всех элементов строки на некоторый коэффициент. Очень полезно! С помощью него можно сократить большие числа в матрице или убрать нули. Множество решений, как обычно, не изменится, а выполнять дальнейшие операции станет удобнее. Главное, чтобы коэффициент не был равен нулю.
- Удаление строк с пропорциональными коэффициентами. Это отчасти следует из предыдущего пункта. Если две или более строки в матрице имеют пропорциональные коэффициенты, то при умножении/делении одной из строк на коэффициент пропорциональности получаются две (или, опять же, более) абсолютно одинаковые строки, и можно убрать лишние, оставив только одну.
- Удаление нулевой строки. Если в ходе преобразований где-то получилась строка, в которой все элементы, включая свободный член, — ноль, то такую строку можно назвать нулевой и выкинуть из матрицы.
- Прибавление к элементам одной строки элементов другой (по соответствующим столбцам), умноженных на некоторый коэффициент. Самое неочевидное и самое важное преобразование из всех. На нем стоит остановиться поподробнее.
Прибавление строки, умноженной на коэффициент
Для простоты понимания стоит разобрать этот процесс по шагам. Берутся две строки из матрицы:
Допустим, необходимо ко второй прибавить первую, умноженную на коэффициент «-2».
Затем в матрице вторая строка заменяется на новую, а первая остается без изменений.
Необходимо заметить, что коэффициент умножения можно подобрать таким образом, чтобы в результате сложения двух строк один из элементов новой строки был равен нулю. Следовательно, можно получить уравнение в системе, где на одну неизвестную будет меньше. А если получить два таких уравнения, то операцию можно проделать еще раз и получить уравнение, которое будет содержать уже на две неизвестных меньше. А если каждый раз превращать в ноль один коэффициент у всех строк, что стоят ниже исходной, то можно, как по ступенькам, спуститься до самого низа матрицы и получить уравнение с одной неизвестной. Это и называется решить систему методом Гаусса.
В общем виде
Пусть существует система. Она имеет m уравнений и n корней-неизвестных. Записать ее можно следующим образом:
Из коэффициентов системы составляется основная матрица. В расширенную матрицу добавляется столбец свободных членов и для удобства отделяется чертой.
- первая строка матрицы умножается на коэффициент k = (-a21/a11);
- первая измененная строка и вторая строка матрицы складываются;
- вместо второй строки в матрицу вставляется результат сложения из предыдущего пункта;
- теперь первый коэффициент в новой второй строке равен a11 × (-a21/a11) + a21 = -a21 + a21 = 0.
Теперь выполняется та же серия преобразований, только участвуют первая и третья строки. Соответственно, в каждом шаге алгоритма элемент a21 заменяется на a31. Потом все повторяется для a41, . am1. В итоге получается матрица, где в строках [2, m] первый элемент равен нулю. Теперь нужно забыть о строке номер один и выполнить тот же алгоритм, начиная со второй строки:
- коэффициент k = (-a32/a22);
- с «текущей» строкой складывается вторая измененная строка;
- результат сложения подставляется в третью, четвертую и так далее строки, а первая и вторая остаются неизменными;
- в строках [3, m] матрицы уже два первых элемента равны нулю.
Алгоритм надо повторять, пока не появится коэффициент k = (-am,m-1/amm). Это значит, что в последний раз алгоритм выполнялся только для нижнего уравнения. Теперь матрица похожа на треугольник, или имеет ступенчатую форму. В нижней строчке имеется равенство amn × xn = bm. Коэффициент и свободный член известны, и корень выражается через них: xn = bm/amn. Полученный корень подставляется в верхнюю строку, чтобы найти xn-1 = (bm-1 — am-1,n×(bm/amn))÷am-1,n-1. И так далее по аналогии: в каждой следующей строке находится новый корень, и, добравшись до «верха» системы, можно отыскать множество решений [x1, . xn]. Оно будет единственным.
Когда нет решений
Если в одной из матричных строк все элементы, кроме свободного члена, равны нулю, то уравнение, соответствующее этой строке, выглядит как 0 = b. Оно не имеет решения. И поскольку такое уравнение заключено в систему, то и множество решений всей системы — пустое, то есть она является вырожденной.
Когда решений бесконечное количество
Может получиться так, что в приведенной треугольной матрице нет строк с одним элементом-коэффициентом уравнения, и одним — свободным членом. Есть только такие строки, которые при переписывании имели бы вид уравнения с двумя или более переменными. Значит, у системы имеется бесконечное число решений. В таком случае ответ можно дать в виде общего решения. Как это сделать?
Все переменные в матрице делятся на базисные и свободные. Базисные — это те, которые стоят «с краю» строк в ступенчатой матрице. Остальные — свободные. В общем решении базисные переменные записываются через свободные.
Для удобства матрица сначала переписывается обратно в систему уравнений. Потом в последнем из них, там, где точно осталась только одна базисная переменная, она остается с одной стороны, а все остальное переносится в другую. Так делается для каждого уравнения с одной базисной переменной. Потом в остальные уравнения, там, где это возможно, вместо базисной переменной подставляется полученное для нее выражение. Если в результате опять появилось выражение, содержащее только одну базисную переменную, она оттуда опять выражается, и так далее, пока каждая базисная переменная не будет записана в виде выражения со свободными переменными. Это и есть общее решение СЛАУ.
Можно также найти базисное решение системы — дать свободным переменным любые значения, а потом для этого конкретного случая посчитать значения базисных переменных. Частных решений можно привести бесконечно много.
Решение на конкретных примерах
Вот система уравнений.
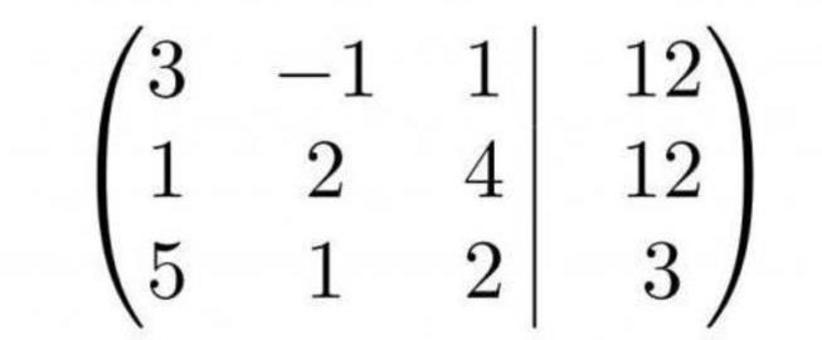
Для удобства лучше сразу составить ее матрицу
Известно, что при решении методом Гаусса уравнение, соответствующее первой строке, в конце преобразований останется неизменным. Поэтому выгодней будет, если левый верхний элемент матрицы будет наименьшим — тогда первые элементы остальных строк после операций обратятся в ноль. Значит, в составленной матрице выгодно будет на место первой строки поставить вторую.
Далее необходимо так изменить вторую и третью строки, чтобы первые элементы стали нулями. Для этого надо сложить их с первой, умноженной их на коэффициент:
Теперь, чтобы не запутаться, необходимо записать матрицу с промежуточными результатами преобразований.
Очевидно, что такую матрицу можно сделать более удобной для восприятия с помощью некоторых операций. Например, из второй строки можно убрать все «минусы», умножая каждый элемент на «-1».
Стоит также заметить, что в третьей строке все элементы кратны трем. Тогда можно сократить строку на это число, умножая каждый элемент на «-1/3» (минус — заодно, чтобы убрать отрицательные значения).
Выглядит гораздо приятнее. Теперь надо оставить в покое первую строку и поработать со второй и третьей. Задача — прибавить к третьей строке вторую, умноженную на такой коэффициент, чтобы элемент a32 стал равен нулю.
k = (-a32/a22) = (-3/7) = -3/7 (если в ходе некоторых преобразований в ответе получилось не целое число, рекомендуется для соблюдения точности вычислений оставить его «как есть», в виде обыкновенной дроби, а уже потом, когда получены ответы, решать, стоит ли округлять и переводить в другую форму записи)
Снова записывается матрица с новыми значениями.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Как видно, полученная матрица уже имеет ступенчатый вид. Поэтому дальнейшие преобразования системы по методу Гаусса не требуются. Что здесь можно сделать, так это убрать из третьей строки общий коэффициент «-1/7».
Теперь все красиво. Дело за малым — записать матрицу опять в виде системы уравнений и вычислить корни
x + 2y + 4z = 12 (1)
Тот алгоритм, по которому сейчас будут находиться корни, называется обратным ходом в методе Гаусса. В уравнении (3) содержится значение z:
Далее возвращаемся ко второму уравнению:
y = (24 — 11×(61/9))/7 = -65/9
И первое уравнение позволяет найти x:
x = (12 — 4z — 2y)/1 = 12 — 4×(61/9) — 2×(-65/9) = -6/9 = -2/3
Такую систему мы имеем право назвать совместной, да еще и определенной, то есть имеющей единственное решение. Ответ записывается в следующей форме:
Пример неопределенной системы
Вариант решения определенной системы методом Гаусса разобран, теперь необходимо рассмотреть случай, если система неопределенная, то есть для нее можно найти бесконечно много решений.
Сам вид системы уже настораживает, потому что количество неизвестных n = 5, а ранг матрицы системы уже точно меньше этого числа, потому что количество строк m = 4, то есть наибольший порядок определителя-квадрата — 4. Значит, решений существует бесконечное множество, и надо искать его общий вид. Метод Гаусса для линейных уравнений позволяет это сделать.
Сначала, как обычно, составляется расширенная матрица.
Вторая строка: коэффициент k = (-a21/a11) = -3. В третьей строке первый элемент — еще до преобразований, поэтому не надо ничего трогать, надо оставить как есть. Четвертая строка: k = (-а41/а11) = -5
Умножив элементы первой строки на каждый их коэффициентов по очереди и сложив их с нужными строками, получаем матрицу следующего вида:
Как можно видеть, вторая, третья и четвертая строки состоят из элементов, пропорциональных друг другу. Вторая и четвертая вообще одинаковые, поэтому одну из них можно убрать сразу, а оставшуюся умножить на коэффициент «-1» и получить строку номер 3. И опять из двух одинаковых строк оставить одну.
Получилась такая матрица. Пока еще не записана система, нужно здесь определить базисные переменные — стоящие при коэффициентах a11 = 1 и a22 = 1, и свободные — все остальные.
Во втором уравнении есть только одна базисная переменная — x2. Значит, ее можно выразить оттуда, записав через переменные x3, x4, x5, являющиеся свободными.
Подставляем полученное выражение в первое уравнение.
Получилось уравнение, в котором единственная базисная переменная — x1. Проделаем с ней то же, что и с x2.
Все базисные переменные, которых две, выражены через три свободные, теперь можно записывать ответ в общем виде.
Также можно указать одно из частных решений системы. Для таких случаев в качестве значений для свободных переменных выбирают, как правило, нули. Тогда ответом будет:
Пример несовместной системы
Решение несовместных систем уравнений методом Гаусса — самое быстрое. Оно заканчивается сразу же, как только на одном из этапов получается уравнение, не имеющее решения. То есть этап с вычислением корней, достаточно долгий и муторный, отпадает. Рассматривается следующая система:
Как обычно, составляется матрица:
| 1 | 1 | -1 | 0 |
| 2 | -1 | -1 | -2 |
| 4 | 1 | -3 | 5 |
И приводится к ступенчатому виду:
| 1 | 1 | -1 | 0 |
| 0 | -3 | 1 | -2 |
| 0 | 0 | 0 | 7 |
После первого же преобразования в третьей строке содержится уравнение вида
не имеющее решения. Следовательно, система несовместна, и ответом будет пустое множество.
Преимущества и недостатки метода
Если выбирать, каким методом решать СЛАУ на бумаге ручкой, то метод, который был рассмотрен в этой статье, выглядит наиболее привлекательно. В элементарных преобразованиях гораздо труднее запутаться, чем в том случается, если приходится искать вручную определитель или какую-нибудь хитрую обратную матрицу. Однако, если использовать программы для работы с данными такого типа, например, электронные таблицы, то оказывается, что в таких программах уже заложены алгоритмы вычисления основных параметров матриц — определитель, миноры, обратная и транспонированная матрицы и так далее. А если быть уверенным в том, что машина посчитает эти значения сама и не ошибется, целесообразней использовать уже матричный метод или формул Крамера, потому что их применение начинается и заканчивается вычислением определителей и обратными матрицами.
Применение
Поскольку решение методом Гаусса представляет из себя алгоритм, а матрица — это, фактически, двумерный массив, его можно использовать при программировании. Но поскольку статья позиционирует себя, как руководство «для чайников», следует сказать, что самое простое, куда метод можно запихнуть — это электронные таблицы, например, Excel. Опять же, всякие СЛАУ, занесенные в таблицу в виде матрицы, Excel будет рассматривать как двумерный массив. А для операций с ними существует множество приятных команд: сложение (складывать можно только матрицы одинаковых размеров!), умножение на число, перемножение матриц (также с определенными ограничениями), нахождение обратной и транспонированной матриц и, самое главное, вычисление определителя. Если это трудоемкое занятие заменить одной командой, можно гораздо быстрее определять ранг матрицы и, следовательно, устанавливать ее совместность или несовместность.