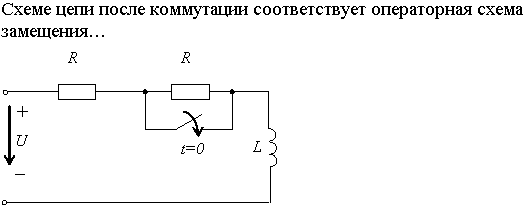
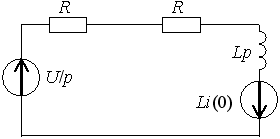
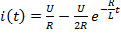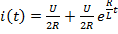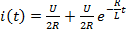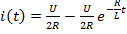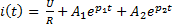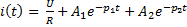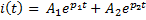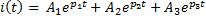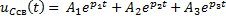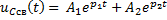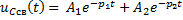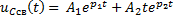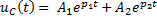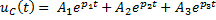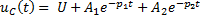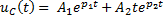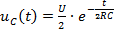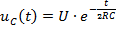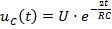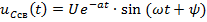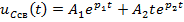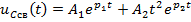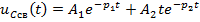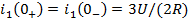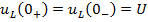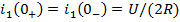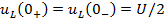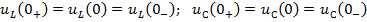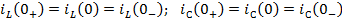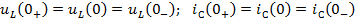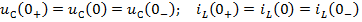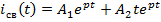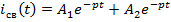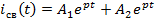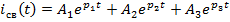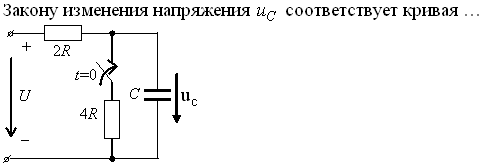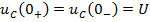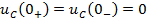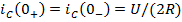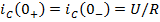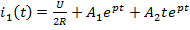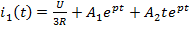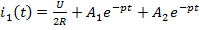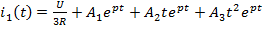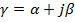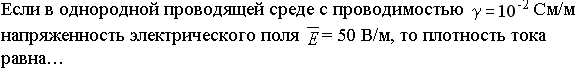Дисциплина «Теоретические основы электротехники»
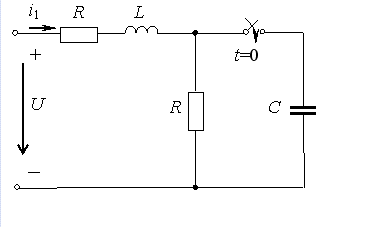
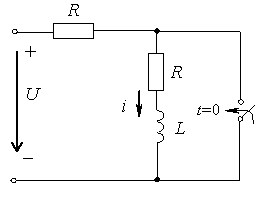
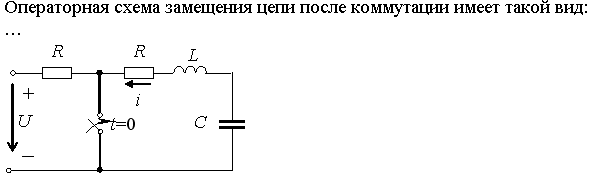
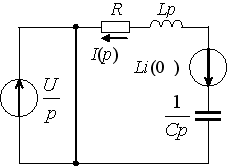
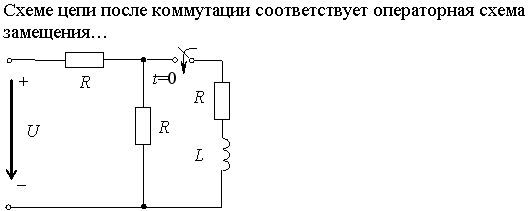
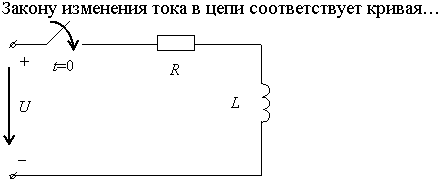
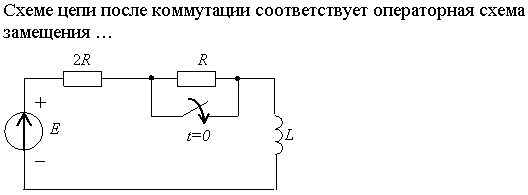
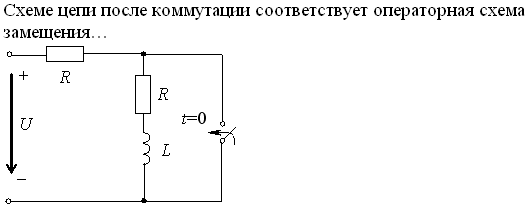
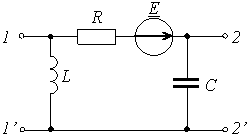
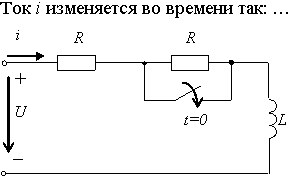
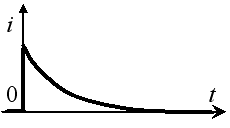
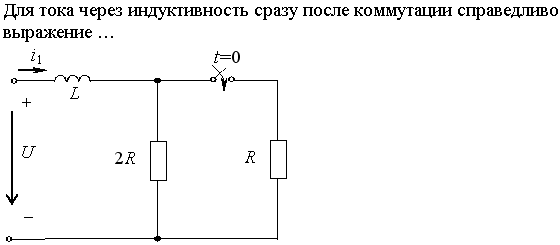
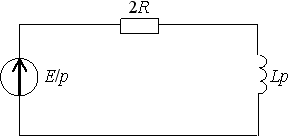
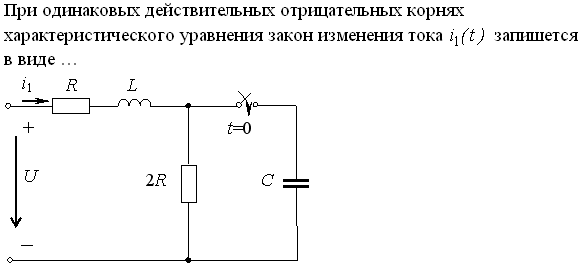
Задание 2.Ток i изменяется во времени так…
1) i(t)=U/2R – (U/2R) e -R/L· t
2) i(t)=0 – (U/2R) e -R/L·t
3) i(t)=U/2R + (U/2R) e -R/L·t
*4) i(t)=0 + (U/2R )e -R/L· t
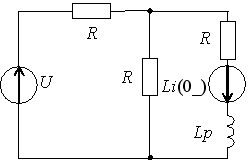
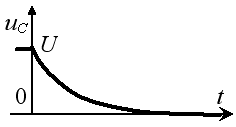
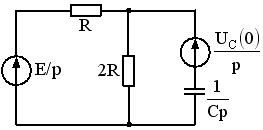
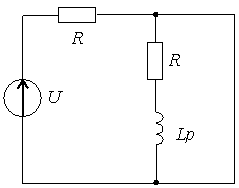
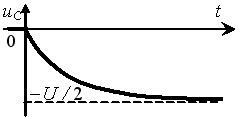
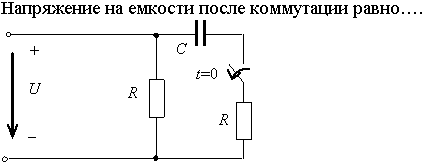
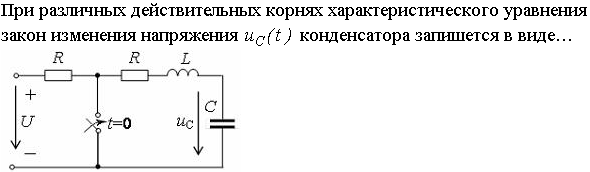
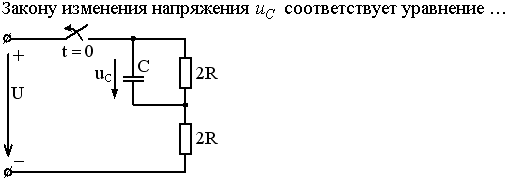
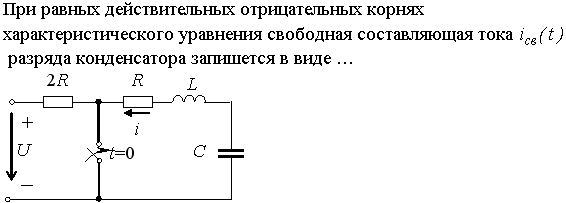
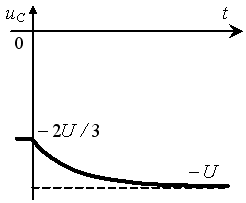
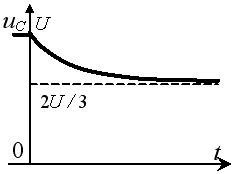
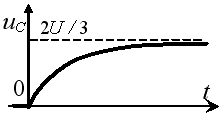
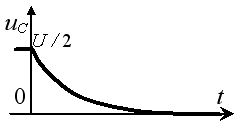
Задание 3.Напряжение на емкости после замыкания ключа равно…
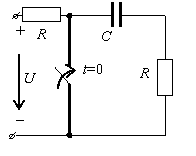
*1)
2)
3)
4)
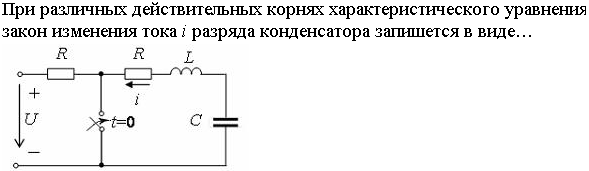
1)
2)
*3)
4)
Задание 6
Задание 7.Если у симметричного четырехполюсника при входном напряжении U1=200 В напряжение на выходе U2=50 В, то при перемене местами входных и выходных зажимов входное и выходное напряжения соответственно равны…
1)
*2)
3)
4)
Задание 9
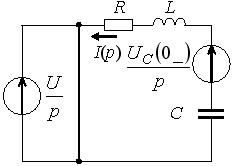
Задание 10
1) 
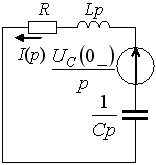
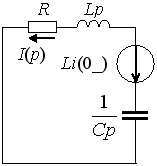
Задание 11
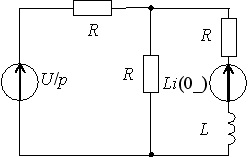
1) 
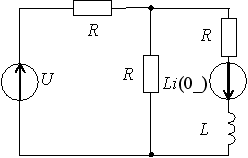
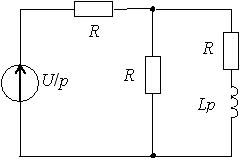
Задание 12
2)
3)
4)
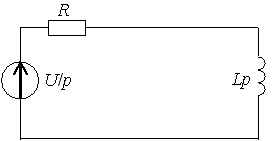
Задание 13
1) 
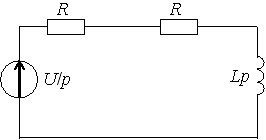
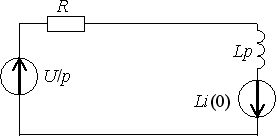
Задание 14
1) 


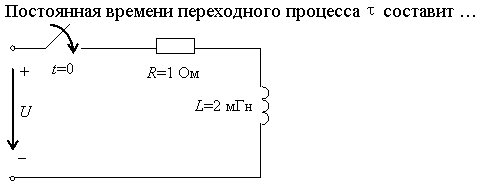
Задание 15. В операторном методе для перехода от изображений токов и напряжений к оригиналам этих величин (функциям времени) используют…
1) матричные преобразования 3) взятие интегралов для вещественных чисел
2) вычисление производных *4) таблицы соответствия изображений и оригиналов,
*1)
2)
3)
4)
Задание 17
Задание 18
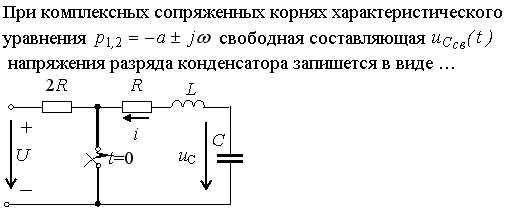
2)
3)
4)
Задание 19
2)
*3)
4)
Задание 20
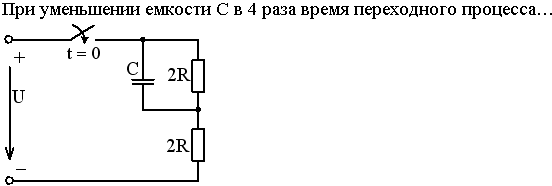
2) уменьшится в 2 раза
3) увеличится в 4 раза
4) увеличится в 2 раза
Задание 21.Законы коммутации записываются выражениями…
1)
2)
3)
*4)
Задание 22
*1) 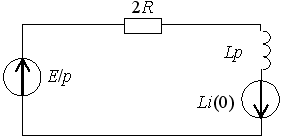
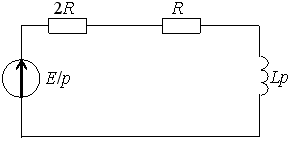
Задание 23
2)
3)
4)
Задание 24
1) 
Задание 25

2)
3)
4)
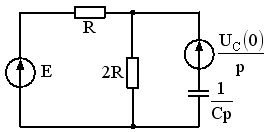
Задание 26
1) 
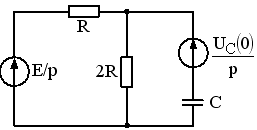
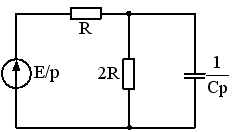
1)
*2)
3)
4)
Задание 28
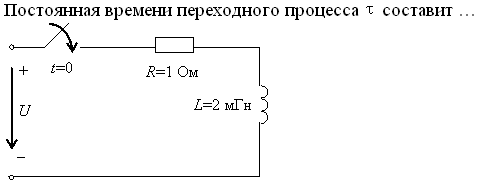
Задание 29
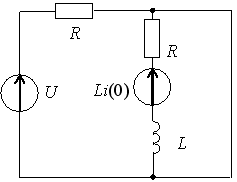
1) 
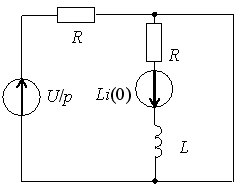
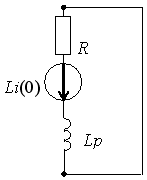
Задание 30
1) 
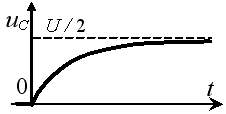
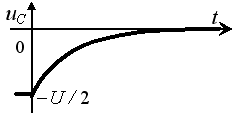
ДИДАКТИЧЕСКАЯ ЕДИНИЦА № 5
Дисциплина «Теоретические основы электротехники»
Задание 1. Для сопротивлений холостого хода и короткого замыкания пассивного четырехполюсника справедливо…
Задание 2.Для линейных четырехполюсников токи I1 и I2 выражаются через напряжения U1 и U2 с помощью уравнений, записанных в …
1) Z – форме 2) H – форме 3) A – форме *4) Y – форме
Задание 3.Еслив длинной линии отсутствует отраженная волна, то линия…
1) нагружена чисто реактивным сопротивлением
2) на конце разомкнута
3) является неискажающей
*4) нагружена волновым сопротивлением
Задание 4.Характеристическими параметрами четырехполюсника являются параметры…
1) Z10 , Z20 2) Z1k , Z2k 3) Zвх1 , Zвх2 *4) Z1с , Z2c ,
Задание 5
Если для симметричного четырехполюсника А = 0,5 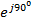
*1) С = –0,125 См; D = 0,5 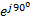
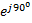
Задание 6
Если для токов и напряжений в начале *1) нагружена волновым сопротивлением
и в конце линии выполняется соотношение 2) на конце замкнута накоротко
U1/U2 = I1/I2, то линия… 3) без искажений, нагрузка любая
4) нагружена чисто реактивным сопротивлением
Задание 7
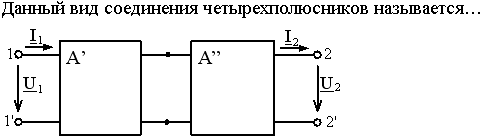
Задание 8.Режим согласованной нагрузки характеризуется…
*1) максимальной мощностью в нагрузке
2) максимальным напряжением на входе
3) максимальным входным током
4) максимальным коэффициентом полезного действия
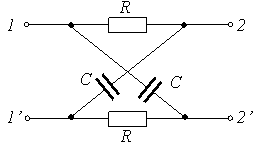
Задание 9.Активный четырехполюсник изображен на схеме…
1) 
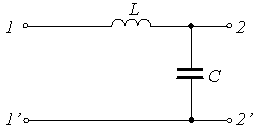
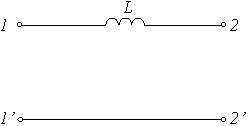
Задание 10.Количество возможных систем параметров, связывающих входные и выходные токи и напряжения четырехполюсника, равно…
1) 3 2) 5 3) 4 *4) 6
Задание 11.Если в середине линии, нагруженной волновым сопротивлением, фаза напряжения отличается от фазы входного напряжения на 60 0 , то фаза напряжения на выходе линии отличается от фазы входного напряжения на…
1) –45 0 *2) 120 0 3) 0 0 4) –90 0
Задание 12
1) 0,02 А/м 2 2) 5000 А/м 2 3) 1 А/м 2 *4) 0,5 А/м 2
Задание 13

Задание 14. Если в линии без потерь со скоростью света распространяется сигнал с частотой f = 10 МГц, то длина волны в линии равна…
*1) 30 км 2) 300 км 3) 3 км 4) 30 км
Задание 15. Для линейных четырехполюсников уравнения в Н –форме позволяют выразить…


3) j 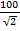
*1) 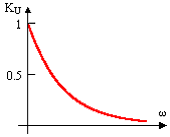
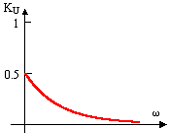
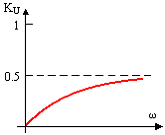
Задание 19.Чтобы записать уравнения симметричного четырехполюсника, связывающие токи и напряжения на его входных и выходных зажимах, необходимо задать ________ параметр(а).
1) 2 *2) 3 3) 4 4) 1
Задание 20
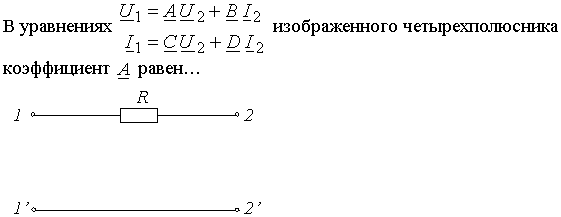
Задание 21.Если в линии без потерь со скоростью света распространяется периодический сигнал, имеющий длину волны 30 м, то период сигнала равен…
1) 1 мс *2) 0,1 мкс 3) 10 мкс 4) 1 мкс
1) сопротивлениями короткого замыкания
2) сопротивлениями холостого хода
Задание 23
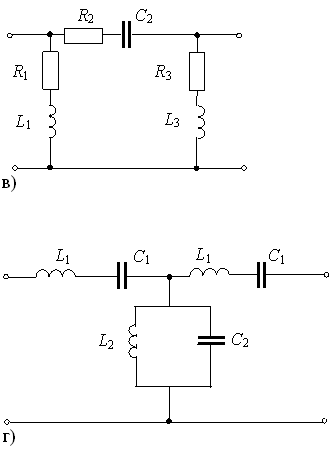
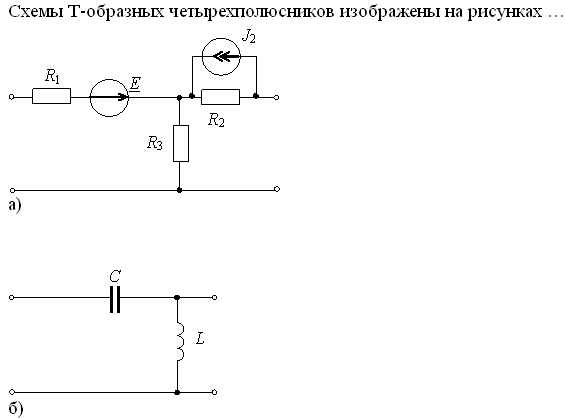

Задание 25.Если поменять местами входные и выходные зажимы пассивного четырехполюсника, то в уравнениях четырехполюсника…
1) изменят знак А и С 3) все А параметры изменят знак
2) ничего не изменится *4) поменяются местами А и D
Видео:Лабораторная работа №5 по физике для 8 класса "Измерение напряжения на различных участках цепи"Скачать

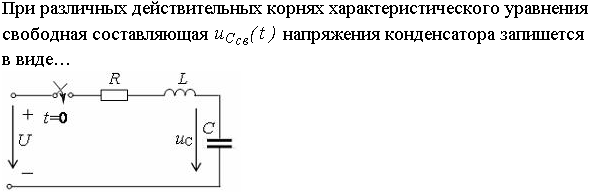
Переходной процесс в цепи второго порядка
5 ПЕРЕХОДНОЙ ПРОЦЕСС В ЦЕПИ ВТОРОГО ПОРЯДКА
Рисунок 5.1 — Схема цепи
Уравнение цепи имеет вид

Дифференцируя обе части выражения (5.1), получим уравнение второго порядка для тока i в цепи:

Однородное уравнение, определяющее свободный ток, можно записать

Введем обозначения 





Ток переходного режима

Ток установившегося режима 

Произвольные постоянные интегрирования A1 и A2 определяют из начальных физических условий: 
Для определения постоянных A1 и A2 надо знать значение тока и всех его производных до (n – 1) включительно в начальный момент времени. В данном случае необходимо знать начальное значение тока и его первой производной. Начальное значение первой производной тока находится из уравнения цепи (5.1) при (t = 0)

где u(0) – значение приложенного напряжения u(t) при t = 0.
Из последнего уравнения получаем

Из уравнения (5.8) для производной тока имеем

Уравнения для нахождения постоянных интегрирования

где 
В качестве примера рассмотрим расчет переходного процесса классическим методом для схемы, изображенной на рис. 5.2. Определить ток
Рисунок 5.2 — Расчетная схема
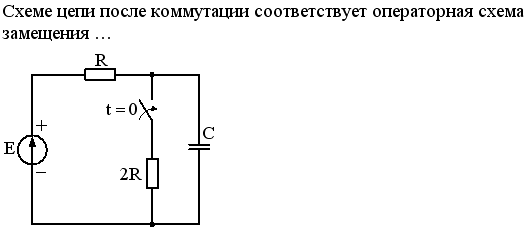
1. Для цепи после коммутации составляются уравнения по I и II законам Кирхгофа.
2. Определяются независимые начальные условия 


3. Искомая величина записывается в виде

4. Установившуюся составляющую определяют из расчета режима цепи после коммутации 
5. Составляется характеристическое уравнение, и определяются его корни

Корни могут быть:
действительные разные p1 и p2; действительные равные p1 = p2 = p; комплексно сопряженные 
где б – коэффициент затухания;
щсв – угловая частота свободных колебаний.
6. В соответствии с полученными корнями характеристического уравнения записывается свободная составляющая:
1) 
2) 
3) 

7. Искомое решение для первого случая

8. Определяются постоянные интегрирования A1 и A2:


Уравнения п.1 для момента времени t = 0 запишутся как

Независимые начальные условия i(0) и 

Для определения 
9. После определения постоянных интегрирования A1 и A2 подставляют их в искомое решение и расчет окончен.
Для определения других токов и напряжений не требуется выполнять все этапы расчета. Можно использовать известные выражения

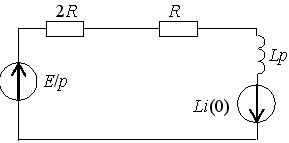
В этом случае приложенное напряжение, а также ток установившегося режима равны нулю:

Для определения произвольных постоянных интегрирования в уравнении необходимо положить: 
Рисунок 5.3 — Расчетная схема
Обозначим 


Напряжения на катушке и конденсаторе

При выводе последнего уравнения учитывалось, что 
5.1 Корни характеристического уравнения
Характер процессов при разряде конденсатора оказывается различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и C.
Рассмотрим возможные случаи.
1. Пусть корни характеристического уравнения вещественны и отличны друг от друга. Это имеет место при условии

Так как 





Ток i не меняет своего направления, т. е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим. Кривые изменения напряжений показаны на рис. 5.5.
Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Портал ТОЭ
6.2 Классический метод расчёта переходных процессов
Анализ переходного процесса в линейной цепи с сосредоточенными параметрами R , L , C (рис. 6.2 ) сводится к решению линейных неоднородных уравнений, выражающих законы Кирхгофа.
где i ( t ) – переходный ток.
Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:
Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.
Решение дифференциального уравнения:
где i пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.
Таким образом здесь используется метод наложения. Физически существует только i ( t ) , а разложение его на i пр и i св является математическим приёмом, облегчающим расчёт переходного процесса.
Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.
Для расчёта свободной составляющей следует найти корни характеристического уравнения p k и n постоянных интегрирования A k .
Если характеристическое уравнение
имеет n различных корней p k ( k = 1 , 2 , … ,n ) , то
Корню p k кратности m k ≥ 1 соответствует слагаемое свободной составляющей вида
Чтобы определить постоянные интегрирования A k , необходимо знать значения искомой величины и всех её производных до ( n − 1) порядка включительно в момент времени t = 0+ . Для их определения используются законы коммутации.
Составление характеристического уравнения
- Составляем уравнение электрического состояния цепи для свободного режима (т.е. при устранении вынужденной (принуждающей) силы). Это соответствует схеме с исключёнными источниками – источники ЭДС закорачиваются, ветви с источниками тока размыкаются.
Например для рис. 6.3 :
где Z вх ( p ) – входное сопротивление схемы относительно двух зажимов, получающихся в результате размыкания любой ветви схемы;
Y вх ( p ) – входная проводимость схемы относительно произвольной пары узлов схемы.
Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.
Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.
Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.
Рассмотрим схему на рис. 6.4 . Три реактивных элемента в упрощённой схеме определяют три независимых начальных условия, т.е. порядок характеристического уравнения равен трём.
Свободный процесс происходит в цепи, освобождённой от источников энергии, поэтому свободные токи не могут протекать сколь угодно долго в цепи, где есть активные элементы. Свободные токи должны затухать, в связи с этим действительные части корней p k характеристического уравнения должны быть отрицательными.
- Так, при наличии одного корня p = − a
🌟 Видео
Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Характеристическое уравнение в ДУСкачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Сопротивление материалов. P-08 (главные напряжения в случае, когда одно из них известно; введение).Скачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Изменение заряда на обкладках конденсатора в цепи CRL без возбуждения. Часть 2.Скачать

Пример 7 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

Лекция 092-1. Расчет переходных процессов операторным методом. Основные понятияСкачать

Классический метод расчета электрической цепи. Пример 2Скачать

Урок 353. Колебательный контурСкачать

✓ Степень с действительным показателем | матан #025 | Борис ТрушинСкачать

Электротехника и электроника. Лекция 5. Переходные процессы в линейных электрических сетяхСкачать

Подготовка к тестам: переходные процессыСкачать