| Название | Для поиска нужного ответа нажимаем ctrlF, и вводим нужный вопрос. |
| Анкор | shpora.docx |
| Дата | 16.01.2018 |
| Размер | 82.93 Kb. |
| Формат файла |  |
| Имя файла | shpora.docx |
| Тип | Документы #14136 |
| Подборка по базе: ГРАММАТИЧЕСКИЕ УПРАЖНЕНИЯ С ОТВЕТАМИ ПО ТЕМЕ ТИПЫ ВОПРОСОВ АНГЛИ, Тест с ответами.doc, Бланк ответа на билет 3.docx, Тест с ответами по теме правление Александра III (1).doc, ПРАКТИЧЕСКАЯ РАБОТА с ответами.docx, Тесты ВБИ новые С.Т. вопр с ответами — копия.docx, с ответами Алынатын протездер.docx.docx, СТОМ.ТЕСТЫ СЕРТИФИК. с ответами — копия.docx, 7_ЗАДАЧА ПОИСКА И СОРТИРОВКИ ИНФОРМАЦИИ docx (1).docx, Практическая работа Деловая этика (с ответами) отпр.docx ДЛЯ ПОИСКА НУЖНОГО ОТВЕТА НАЖИМАЕМ Ctrl+F, И ВВОДИМ НУЖНЫЙ ВОПРОС.
Система эконометрических уравнений является идентифицируемой, если идентифицируемо каждое уравнение системы Система эконометрических уравнений является неидентифицируемой, если неидентифицируемо хотя бы одно уравнение системы Система эконометрических уравнений является сверхидентифицируемой, если сверхидентифицируемо хотя бы одно уравнение системы Сверхидентифицируемые
заданная система одновременных уравнений и структурных формы преобразуются в приведенную форму оценки параметров приведенной формы находится традиционным методом наименьших квадратов определение расчетных значений эндогенных переменных, которые выступают в качестве факторов в структурной
Этот алгоритм соответствует ______ методу наименьших квадратов.
1 служит для проверки гипотезы о гомоскедастичности остатков —b 2 служит для проверки гипотезы об отсутствии автокорреляции остатков — c 3 служит для оценки мультиколлинеарности факторов- d
Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапе спецификация модели В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно … сумме Влияние фиктивной переменной наклона на регрессивную модель состоит в …
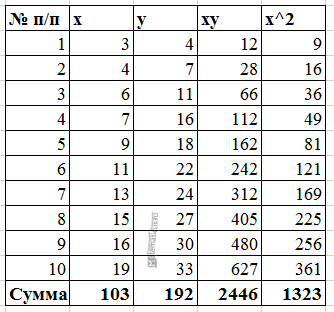
Если коэффициент регрессии является существенным, то для него выполняются условия ….(несколько правильных ответов) МНК 2Нелинейная модель, линейная относительно параметров 4Нелинейная модель внутренние нелинейные 3Нелинейная модель нелинейная относительно параметров (внутренне линейная) 1.Термин эконометрика был введен (Фришем) 11.Медиана в ряду распределения с четным числом членов ряда равна (полусумме двух срединных членов) 12.Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим . (тесноту и форму зависимости между признаками) 20.Корреляция подразумевает наличие связи между . (переменными) 21.Принцип спецификации модели, лежащий в основании классификации: экономические модели; эконометрические модели (включение случайных возмущений) 23.Для описания тесноты (силы) связи между зависимой переменной и фактором (факторами) проводят расчет. (коэффициент корреляции) 24.Среднее квадратичное отклонение (показывает в среднем, на сколько отклоняются значения показателя от среднего значения) 25.Значение признака, повторяющееся с наибольшей частотой, называется (модой) 26.Случайная составляющая характеризует ( отклонение модельного значения результирующей переменной от наблюдаемого) 27.Укажите правильные варианты ответов относительно числа переменных включаемых в уравнение регрессии(несколько зависимых и одна не зависимая переменных, одна зависимая и несколько независимых переменных) 28.Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно . ( 10%) 29.Верификация модели заключается в( сопоставлении модельных и реальных данных) 30.Этап параметризации модели включает в себя.. (оценку параметров модели) 31.определяется _________ показателей x и y.( Ковариация) 32.В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно . (сумме) 33.Один из этапов построения экономической модели, на котором проверяются статистические свойства построенной модели, называется. (верификацией модели.) 34.По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются на (эндогенные и экзогенные) 35.Коэффициент корреляции это: (относительная мера взаимосвязи переменных) .Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено . (неоднородностью выборки) 37. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой.. (спецификации) 38Средне квадратическое отклонение исчисляется как (корень квадратный из дисперсии) 39.Разность фактического и теоретического значений результирующей переменной регрессионной модели называется. (остатком) 40.Статистический показатель дает оценку свойства изучаемого явления: (количественную) 41.Под верификацией модели понимается (проверка адекватности модели) 42.Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапе (спецификация модели) 43.Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,25 (3,5) 44.Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетом (ошибки выборки) 45.Принцип спецификации модели, лежащий в основании классификации: статические модели; динамические модели (датирование переменных) 46.Средняя арифметическая величина — это отношение( суммы значений показателя к объему совокупности) 47.Экономические модели относятся к классу ___________ экономико-математических моделей (стохастических) 48.Средняя геометрическая — это: (корень из произведения индивидуальных показателей) 49.При анализе взаимосвязи признаков в экономической модели используют корреляционное отношение, подсчитанное на основе( аналитической группировки) 50.Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените? (средняя арифметическая) 51.Причинами нарушения предпосылок МНК могут являться .. (наличие неучтенного в уравнении существенного фактора ,наличие в уравнении фиктивных переменных.) 52.Модель, содержащая фиктивную переменную, относится к ____ модели. (Регрессионной) 53.МНК позволяет получить состоятельные и несмещенные оценки параметров системы: (независимых уравнений) При каком значении линейного коэффициента корреляции связь между признаками Y и X можно считать тесной (сильной)( 0,975) 54.С увеличением объема выборки длина доверительного интервала индивидуального значения эндогенной переменной (уменьшается) 55.Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R 2 для модели парной регрессии равен: (единице) Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать  Метод наименьших квадратов регрессияМетод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид y=ax+b a, b – коэффициенты линейного уравнения регрессии; x – независимая переменная; y – зависимая переменная. Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов: частные производные функции приравниваем к нулю отсюда получаем систему линейных уравнений Формулы определения коэффициентов уравнения линейной регрессии: Также запишем уравнение регрессии для квадратной нелинейной функции: Система линейных уравнений регрессии полинома n-ого порядка: Формула коэффициента детерминации R 2 : Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели): Чем меньше ε, тем лучше. Рекомендованный показатель ε Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
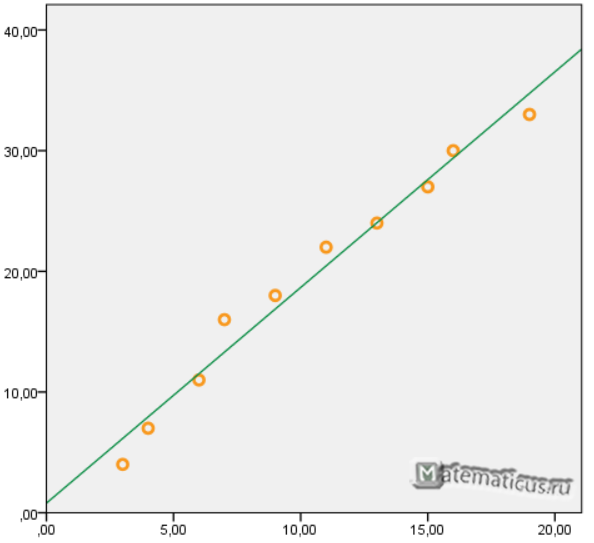
Решение Расчеты значений суммы, произведения x и у приведены в таблицы. Расчет коэффициентов линейной регрессии: при этом средняя ошибка аппроксимации равна: ε=11,168% Получаем уравнение линейной регрессии с помощью метода наименьших квадратов: y=1,7871x+0,79 График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек Коэффициент корреляции равен 0,988 Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать  Классический метод наименьших квадратов для модели множественной регрессии. Метод КрамераВ общем виде линейную модель множественной регрессии можно записать следующим образом: где yi – значение i-ой результативной переменной, x1i…xmi – значения факторных переменных; β0…βm – неизвестные коэффициенты модели множественной регрессии; εi – случайные ошибки модели множественной регрессии. В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений y˜ (рассчитанных на основании построенной модели регрессии) была бы минимальной. Матричная форма функционала F метода наименьших квадратов: В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0…βm, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1): Общий вид стационарной системы уравнений для функции (1): Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии: Оценим с помощью метода наименьших квадратов неизвестные параметры линейной модели двухфакторной регрессии: Чтобы рассчитать оценки неизвестных коэффициентов β0,β1 и β2данной двухфакторной модели регрессии, необходимо минимизировать функционал F вида: Для определения экстремума функции нескольких переменных, частные производные по этим переменным приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для модели множественной линейной регрессии с двумя переменными: В результате элементарных преобразований данной стационарной системы уравнений получим систему нормальных уравнений: Данная система называется системой нормальных уравнений относительно коэффициентов Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты Рассмотрим подробнее метод Крамера решения квадратных систем нормальных уравнений. Единственное решение квадратной системы линейных уравнений определяется по формуле: где Δ – основной определитель квадратной системы линейных уравнений; Δj – определитель, полученный из основного определителя путём замены j-го столбца на столбец свободных членов. При использовании метода Крамера возможно возникновение следующих ситуаций: 1) если основной определитель системы Δ равен нулю и все определители Δj также равны нулю, то данная система имеет бесконечное множество решений; 2) если основной определитель системы Δ равен нулю и хотя бы один из определителей Δj также равен нулю, то система решений не имеет. 📹 ВидеоМетод наименьших квадратов (МНК)Скачать  Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать  ЦОС Python #1: Метод наименьших квадратовСкачать  Метод наименьших квадратовСкачать  Метод наименьших квадратов. Квадратичная аппроксимацияСкачать  Метод наименьших квадратовСкачать  Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать  Метод Наименьших Квадратов (МНК)Скачать  Построение уравнения линейной регрессии методом наименьших квадратов.Скачать  Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать  Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать  11 1 Метод наименьших квадратов ВведениеСкачать  К первой паре / Эконометрика. Лекция 2. Метод наименьших квадратов. Модель парной регрессииСкачать  Метод наименьших квадратов. Регрессионный анализ.Скачать  Метод наименьших квадратов Построение уравнения парной регрессии #мнк #регрессия #корреляцияСкачать  Парная регрессия: линейная зависимостьСкачать  Митин И. В. - Обработка результатов физического эксперимента - Метод наименьших квадратовСкачать  СКМ 2021-04-27-1 Аппроксимация. Линейный метод наименьших квадратовСкачать  |

 определяется _________ показателя x.
определяется _________ показателя x. определяется _________ показателя x.
определяется _________ показателя x. определяется _________ показателя x.
определяется _________ показателя x. определяется _________ показателей x и y.
определяется _________ показателей x и y.
 и коэффициент корреляции
и коэффициент корреляции . Чему равна выборочная ковариация:
. Чему равна выборочная ковариация: .
. .
.


 . Определите спецификацию модели.
. Определите спецификацию модели.
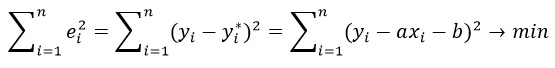
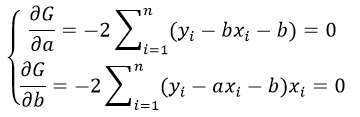
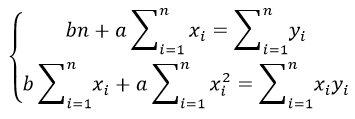
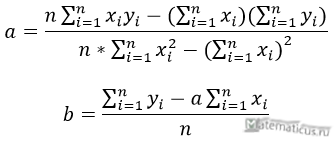
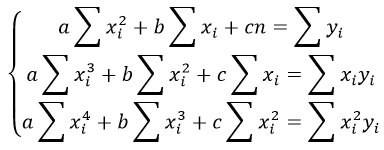
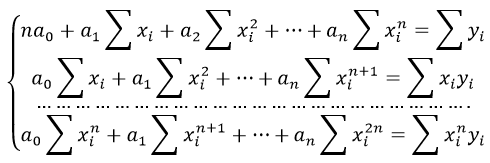
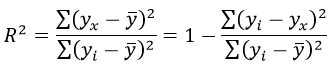
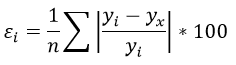
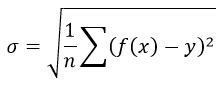
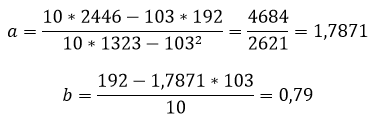
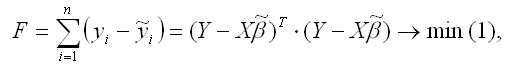
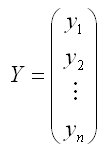 – случайный вектор-столбец значений результативной переменной размерности (n*1);
– случайный вектор-столбец значений результативной переменной размерности (n*1); – матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;
– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;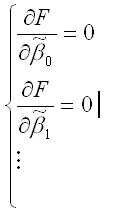
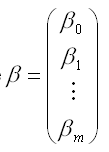 – вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);
– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);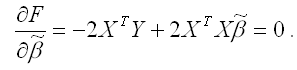
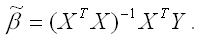
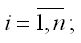
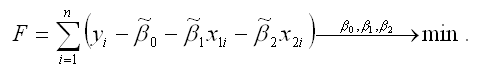
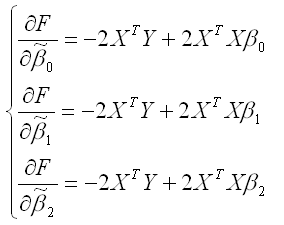
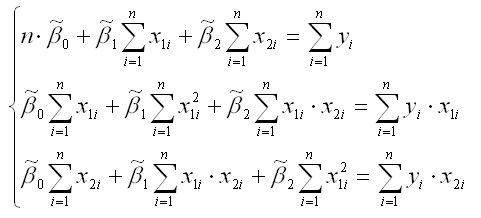
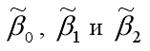 для модели регрессии yi=β0+β1x1i+β2x2i+εi.
для модели регрессии yi=β0+β1x1i+β2x2i+εi.