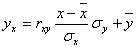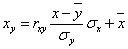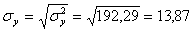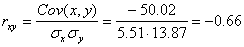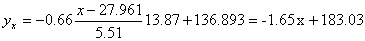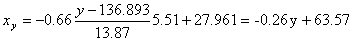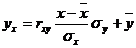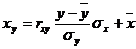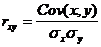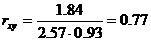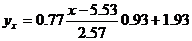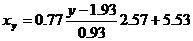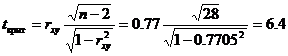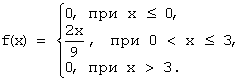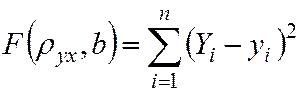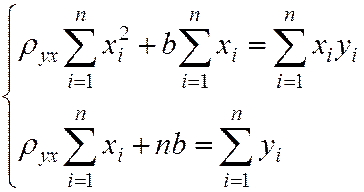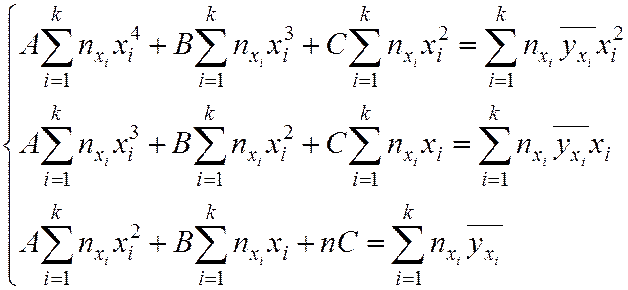Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
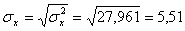
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

При построении выборочного уравнения прямой линии регрессии вычислены выборочный
ЗАДАЧИ ИЗ ТЕСТОВ С РЕШЕНИЯМИ
Задача 1. Из урны, в которой находятся 12 белых и 10 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна…
Воспользуемся формулой 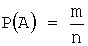

Задача 2. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна…
Воспользуемся формулой 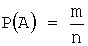
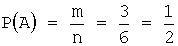
Задача 3. Из урны, в которой находятся 6 черных и 10 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут белыми, равна…
Воспользуемся формулой 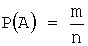
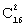
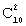
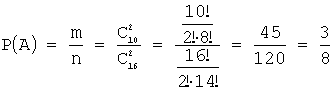
Задача 4. Два предприятия производят разнотипную продукцию. Вероятности их банкротства в течение года равны 0,1 и 0,2 соответственно. Тогда вероятность того, что в течение года обанкротится хотя бы одно предприятие, равна…
Введем обозначения событий: A 1 — обанкротится первое предприятие; A 2 — обанкротится второе предприятие; A — обанкротится хотя бы одно предприятие; 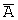
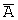
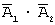
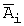
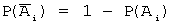
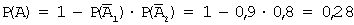
Задача 5. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,7 и 0,85 соответственно. Тогда вероятность того, что в цель попадет только один стрелок, равна …
Введем обозначения событий: A 1 — в цель попадет первый стрелок, A 2 — в цель попадет второй стрелок, A — в цель попадет только один стрелок. Тогда 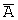
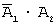
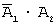
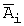
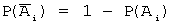

Задача 6. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,9, 0,8 и 0,7. Тогда вероятность того, что в течение рабочего дня будут работать безотказно все три элемента, равна…
Введем обозначения событий: Ai — в течение рабочего дня безотказно работает i — ый элемент, A – в течение рабочего дня работают безотказно все три элемента. Тогда A = A 1 · A 2 · A 3 . Так как, по условию задачи, события A 1 , A 2 и A 3 независимы, то P ( A )= P ( A 1 · A 2 · A 3 )=
Задача 7. В первой урне 3 черных и 7 белых шаров. Во второй урне 4 белых и 6 черных шаров. В третьей урне 11 белых и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: 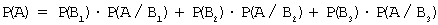
Здесь: 
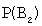
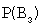
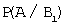

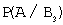
Тогда 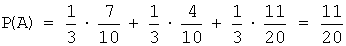
Задача 8. В первой урне 6 черных и 4 белых шара. Во второй урне 2 белых и 18 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар извлечен из первой урны, равна…
Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: 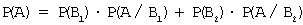
Здесь: 
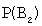
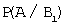

Тогда 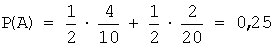
Теперь вычислим условную вероятность того, что шар извлечен из первой урны, если он оказался белым, по формуле Байеса:
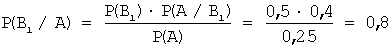
Задача 9. С первого станка на сборку поступает 45%, со второго – 55% всех деталей. Среди деталей первого станка 90% стандартных, второго – 80%. Тогда вероятность того, что взятая наудачу деталь окажется нестандартной, равна …
Для вычисления вероятности события A (взятая наудачу деталь окажется нестандартной) применим формулу полной вероятности: 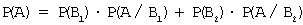

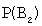
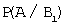
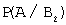
Тогда
P ( A )=0,45(1-0,9)+0,55(1-0,8)=0,045+0,11=0,155.
Задача 10. С первого станка на сборку поступает 20%, со второго – 80% всех деталей. Среди деталей первого станка 90% стандартных, второго – 70%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что эта деталь изготовлена на первом станке, равна …
Предварительно вычислим вероятности события A (взятая наудачу деталь окажется стандартной) по формуле полной вероятности: 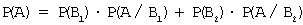
Здесь: 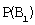
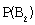
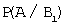

Тогда 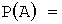
Теперь вычислим условную вероятность того, что деталь изготовлена на первом станке, если она оказалась стандартной, по формуле Байеса:
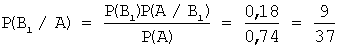
Задача 11. Дискретная случайная величина задана законом распределения вероятностей
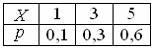
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 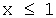
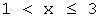
в) при 
F ( x )= P ( X =1)+ P ( X =3)=0,1+0,3=0,4,
г) при x > 5,
F(x)=P(X=1)+ P(X=3)+P(X=5)+P(X=6)= 0,1+0,3+0,6=1.
Следовательно,
Задача 12. Дискретная случайная величина задана законом распределения вероятностей

Тогда значения a и b могут быть равны…
Так как сумма вероятностей возможных значений равна 1, то a + b =1-0,1-0,2=0,7. Этому условию удовлетворяет ответ: a =0,4, b =0,3.
Задача 13. Даны две независимые дискретные случайные величины X и Y :
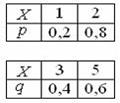
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда ответ:
Задача 14. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,2. Тогда математическое ожидание дискретной случайной величины X — числа появлений события A в n =100 проведенных испытаниях, равно…
Случайная величина X подчиняется биномиальному закону распределения вероятностей. Поэтому M ( X )= np =100∙0,2=20.
Задача 15. Непрерывная случайная величина задана функцией распределения вероятностей:
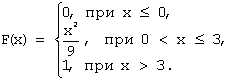
Тогда плотность распределения вероятностей имеет вид…
Плотность распределения вероятностей непрерывной случайной величины вычисляется по формуле: f ( x )= F ’( x ). Тогда 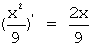
Задача 16. Непрерывная случайная величина X задана плотностью распределения вероятностей 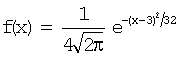
Плотность распределения вероятностей нормально распределенной случайной величины имеет вид: 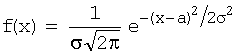
Задача 17. Дискретная случайная величина задана законом распределения вероятностей
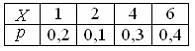
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 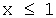
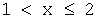
в) при 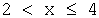
F ( x )= P ( X =1)+ P ( X =2)=0,2+0,1=0,3,
г) при 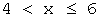
F ( x )= P ( X =1)+ P ( X =2)+ P ( X =4)=0,2+0,1+0,3=0,6,
д) при x > 6,
F(x)=P(X=1)+ P(X=2)+P(X=4)+P(X=6)=1.
Следовательно,
Задача 18. Даны две независимые дискретные случайные величины X и Y :
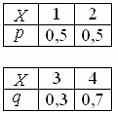
Решение.
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда правильным будет ответ:

Задача 19. Основная гипотеза имеет вид H 0 : σ 2 =4. Тогда конкурирующей может являться гипотеза…
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию σ 2 =4 противоречит H 1 :σ 2 >4.
Задача 20. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,85 и выборочные средние квадратические отклонения σ X =3,2 σ Y =1,6. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 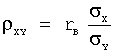
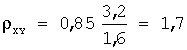
Задача 21. Выборочное уравнение парной регрессии имеет вид y =-1,56-2,3 x .
Тогда выборочный коэффициент корреляции может быть равен…
(Варианты ответа: |1,56 | — 0,87 | — 2,3 | 0,87)
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,87.
Задача 22. Выборочное уравнение парной регрессии имеет вид y =6-3 x . Тогда выборочный коэффициент корреляции может быть равен…
( Варианты ответов: 0,9 | -3,0 | 6,0 | — 0,9 )
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,9 .
Задача 23. Выборочное уравнение парной регрессии имеет вид y =-5+2 x . Тогда выборочный коэффициент регрессии равен…
Если выборочное уравнение парной регрессии имеет вид y =α+β x , то выборочный коэффициент регрессии равен β. То есть β=2.
Задача 24. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,75 и выборочные средние квадратические отклонения σ X =1,1 σ Y =2,2. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 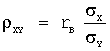
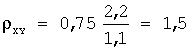
Задача 25. Мода вариационного ряда 1,2,2,3,3,3,4 равна…
Модой вариационного ряда называется варианта, имеющая наибольшую частоту. Такой вариантой является варианта 3, частота которой равна
Задача 26. Медиана вариационного ряда 3,4,5,6,7,12 равна…
Медианой вариационного ряда называется варианта, расположенная в середине вариационного ряда. Так как в середине ряда располагаются две варианты: 5 и 6, то медиана равна их средней арифметической 5,5.
Задача 27. Размах варьирования вариационного ряда 3,5,5,7,9,10,16 равен…
Размах варьирования вариационного ряда определяется как R = xmax — xmin , то есть R =16-3=13.
Задача 28. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 10, 12. Тогда несмещенная оценка дисперсии равна…
Несмещенная оценка дисперсии вычисляется по формуле: 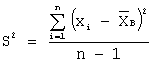
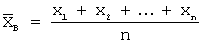
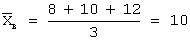

Задача 29. Из генеральной совокупности извлечена выборка объема n =20:
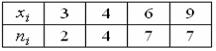
Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 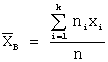
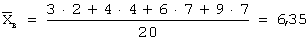
Задача 30. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 11, 13, 14. Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 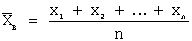

Задача 31. Дана интервальная оценка (8,45;9,15) математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна…
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна 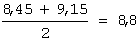
Задача 32. Дана интервальная оценка (10,45;11,55) математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна…
Точность интервальной оценки ( a ; b ) определяется как 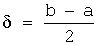
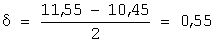
Задача 33. Из генеральной совокупности извлечена выборка объема n =50, гистограмма частот которой имеет вид:
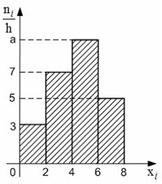
Тогда значение a равно…
Так как объем выборки вычисляется как n =( a +7+5+3) h , то a =50/2-7-5-3=10.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Выборочное уравнение прямой линии регрессии
Рассмотрим выборочное уравнение прямой линии среднеквадратичной регрессии Y на X в виде
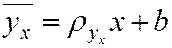
где 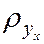
Подберём параметры 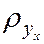
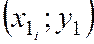
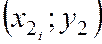

При использовании метода наименьших квадратов (МНК) смысл этого требования интерпретируется так: сумма квадратов отклонений должна быть минимальной. Под отклонением понимают разность 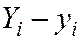
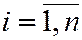
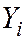
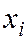
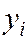
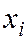
Запишем это требование в виде функции:
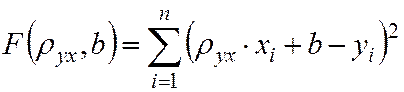
Для отыскания минимума функции 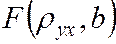
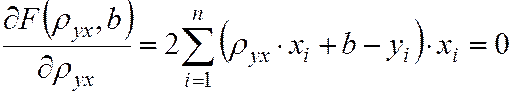
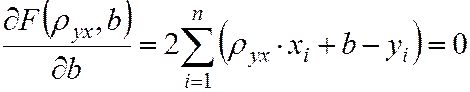
Выполнив преобразования, получим систему
Решив данную систему, найдём искомые параметры
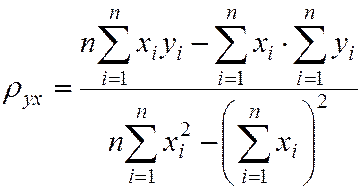
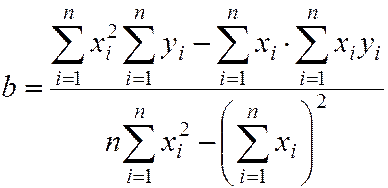
Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y.
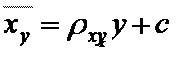
Пример. Найти уравнение прямой линии регрессии по данным наблюдений:
| X | 1,00 | 1,50 | 3,00 | 4,50 | 5,00 |
| Y | 1,25 | 1,40 | 1,50 | 1,75 | 2,25 |
Составляем расчётную таблицу:
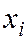 | 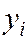 | 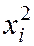 |  |
| 1,00 | 1,25 | 1,00 | 1,250 |
| 1,50 | 1,40 | 2,25 | 2,100 |
| 3,00 | 1,50 | 9,00 | 4,500 |
| 4,50 | 1,75 | 20,25 | 4,875 |
| 5,00 | 2,25 | 25,00 | 11,250 |
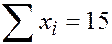 | 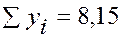 | 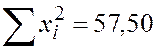 |  |
Находим неизвестные параметры из уравнения прямой линии регрессии:
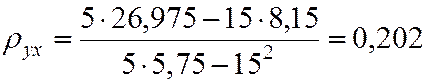
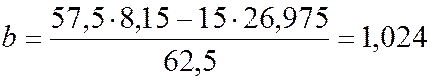
Записываем искомое уравнение:
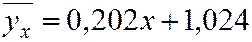
Если данные наблюдений представлены в виде корреляционнной таблицы 6.1, то 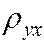
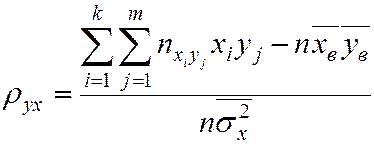
Умножим обе части равенства (7.6) на дробь 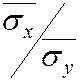
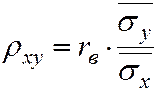
Отсюда уравнение (7.3) можно записать через rв:
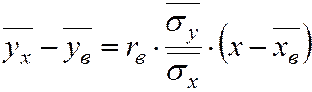
Аналогично уравнение (7.5) примет вид

Выборочное уравнение нелинейной регрессии
Функции регрессии Y на X могут иметь вид, например, параболической корреляции второго порядка
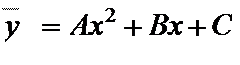
параболической корреляции третьего порядка

где A, B, C, D – неизвествные параметры.
Определить неизвестные параметры можно МНК. Для уравнения (7.9) неизвестные параметры A, B, C находят из решения системы линейных уравнений:
Пример. В. Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике», стр. 276.
Элементы дисперсионного анализа
Общие сведения
Дисперсионный анализ применяют, чтобы установить:
— оказывает ли существенное влияние некоторый качественный фактор 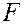
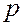
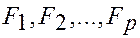
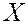
— являются ли однородными несколько совокупностей, т.к. однородные совокупности можно объединить в одну и тем самым получить о ней более полную информацию.
Суть дисперсионного анализасостоит в сравнении «факторной дисперсии» (т.е. межгрупповой), обусловленной воздействием фактора, и «остаточной дисперсии» (т.е. внутригрупповой), порождаемой случайными причинами по критерию Фишера-Снедекора.
Различают дисперсионный анализ:
— однофакторный, если исследуется влияние одного фактора на изучаемую СВ;
— многофакторный, если исследуется воздействие нескольких факторов.
Рассмотрим случай однофакторного дисперсионного анализа, когда на изучаемую величину 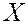
💥 Видео
Метод наименьших квадратов. Линейная аппроксимацияСкачать

Линейная регрессияСкачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Математика #1 | Корреляция и регрессияСкачать

Парная регрессия: линейная зависимостьСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

#25. Метод главных компонент (Principal Component Analysis) | Машинное обучениеСкачать

РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать
Видеоурок "Параметрические уравнения прямой"Скачать

Эконометрика. Линейная парная регрессияСкачать

11. Прямая в пространстве и ее уравненияСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать

Видеоурок "Общие уравнения прямой"Скачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать