ЗАДАЧИ ИЗ ТЕСТОВ С РЕШЕНИЯМИ
Задача 1. Из урны, в которой находятся 12 белых и 10 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна…
Воспользуемся формулой 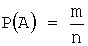

Задача 2. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна…
Воспользуемся формулой 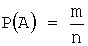
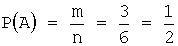
Задача 3. Из урны, в которой находятся 6 черных и 10 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут белыми, равна…
Воспользуемся формулой 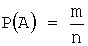
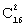
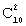
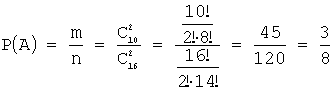
Задача 4. Два предприятия производят разнотипную продукцию. Вероятности их банкротства в течение года равны 0,1 и 0,2 соответственно. Тогда вероятность того, что в течение года обанкротится хотя бы одно предприятие, равна…
Введем обозначения событий: A 1 — обанкротится первое предприятие; A 2 — обанкротится второе предприятие; A — обанкротится хотя бы одно предприятие; 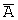
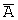
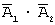
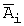
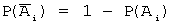
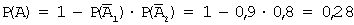
Задача 5. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,7 и 0,85 соответственно. Тогда вероятность того, что в цель попадет только один стрелок, равна …
Введем обозначения событий: A 1 — в цель попадет первый стрелок, A 2 — в цель попадет второй стрелок, A — в цель попадет только один стрелок. Тогда 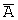
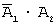
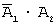
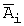
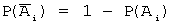

Задача 6. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,9, 0,8 и 0,7. Тогда вероятность того, что в течение рабочего дня будут работать безотказно все три элемента, равна…
Введем обозначения событий: Ai — в течение рабочего дня безотказно работает i — ый элемент, A – в течение рабочего дня работают безотказно все три элемента. Тогда A = A 1 · A 2 · A 3 . Так как, по условию задачи, события A 1 , A 2 и A 3 независимы, то P ( A )= P ( A 1 · A 2 · A 3 )=
Задача 7. В первой урне 3 черных и 7 белых шаров. Во второй урне 4 белых и 6 черных шаров. В третьей урне 11 белых и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: 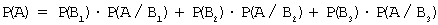
Здесь: 
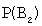
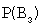
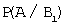

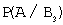
Тогда 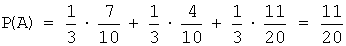
Задача 8. В первой урне 6 черных и 4 белых шара. Во второй урне 2 белых и 18 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар извлечен из первой урны, равна…
Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: 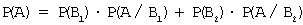
Здесь: 
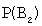
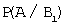

Тогда 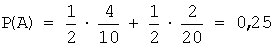
Теперь вычислим условную вероятность того, что шар извлечен из первой урны, если он оказался белым, по формуле Байеса:
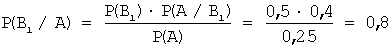
Задача 9. С первого станка на сборку поступает 45%, со второго – 55% всех деталей. Среди деталей первого станка 90% стандартных, второго – 80%. Тогда вероятность того, что взятая наудачу деталь окажется нестандартной, равна …
Для вычисления вероятности события A (взятая наудачу деталь окажется нестандартной) применим формулу полной вероятности: 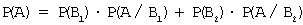

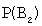
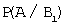
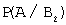
Тогда
P ( A )=0,45(1-0,9)+0,55(1-0,8)=0,045+0,11=0,155.
Задача 10. С первого станка на сборку поступает 20%, со второго – 80% всех деталей. Среди деталей первого станка 90% стандартных, второго – 70%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что эта деталь изготовлена на первом станке, равна …
Предварительно вычислим вероятности события A (взятая наудачу деталь окажется стандартной) по формуле полной вероятности: 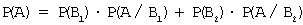
Здесь: 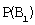
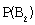
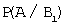

Тогда 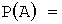
Теперь вычислим условную вероятность того, что деталь изготовлена на первом станке, если она оказалась стандартной, по формуле Байеса:
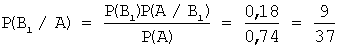
Задача 11. Дискретная случайная величина задана законом распределения вероятностей
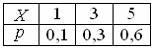
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 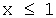
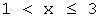
в) при 
F ( x )= P ( X =1)+ P ( X =3)=0,1+0,3=0,4,
г) при x > 5,
F(x)=P(X=1)+ P(X=3)+P(X=5)+P(X=6)= 0,1+0,3+0,6=1.
Следовательно,
Задача 12. Дискретная случайная величина задана законом распределения вероятностей

Тогда значения a и b могут быть равны…
Так как сумма вероятностей возможных значений равна 1, то a + b =1-0,1-0,2=0,7. Этому условию удовлетворяет ответ: a =0,4, b =0,3.
Задача 13. Даны две независимые дискретные случайные величины X и Y :
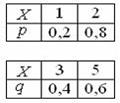
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда ответ:
Задача 14. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,2. Тогда математическое ожидание дискретной случайной величины X — числа появлений события A в n =100 проведенных испытаниях, равно…
Случайная величина X подчиняется биномиальному закону распределения вероятностей. Поэтому M ( X )= np =100∙0,2=20.
Задача 15. Непрерывная случайная величина задана функцией распределения вероятностей:
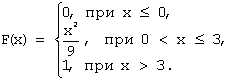
Тогда плотность распределения вероятностей имеет вид…
Плотность распределения вероятностей непрерывной случайной величины вычисляется по формуле: f ( x )= F ’( x ). Тогда 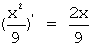
Задача 16. Непрерывная случайная величина X задана плотностью распределения вероятностей 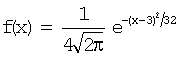
Плотность распределения вероятностей нормально распределенной случайной величины имеет вид: 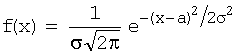
Задача 17. Дискретная случайная величина задана законом распределения вероятностей
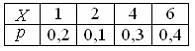
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 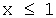
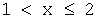
в) при 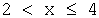
F ( x )= P ( X =1)+ P ( X =2)=0,2+0,1=0,3,
г) при 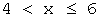
F ( x )= P ( X =1)+ P ( X =2)+ P ( X =4)=0,2+0,1+0,3=0,6,
д) при x > 6,
F(x)=P(X=1)+ P(X=2)+P(X=4)+P(X=6)=1.
Следовательно,
Задача 18. Даны две независимые дискретные случайные величины X и Y :
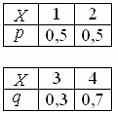
Решение.
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда правильным будет ответ:

Задача 19. Основная гипотеза имеет вид H 0 : σ 2 =4. Тогда конкурирующей может являться гипотеза…
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию σ 2 =4 противоречит H 1 :σ 2 >4.
Задача 20. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,85 и выборочные средние квадратические отклонения σ X =3,2 σ Y =1,6. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 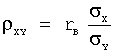
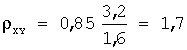
Задача 21. Выборочное уравнение парной регрессии имеет вид y =-1,56-2,3 x .
Тогда выборочный коэффициент корреляции может быть равен…
(Варианты ответа: |1,56 | — 0,87 | — 2,3 | 0,87)
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,87.
Задача 22. Выборочное уравнение парной регрессии имеет вид y =6-3 x . Тогда выборочный коэффициент корреляции может быть равен…
( Варианты ответов: 0,9 | -3,0 | 6,0 | — 0,9 )
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,9 .
Задача 23. Выборочное уравнение парной регрессии имеет вид y =-5+2 x . Тогда выборочный коэффициент регрессии равен…
Если выборочное уравнение парной регрессии имеет вид y =α+β x , то выборочный коэффициент регрессии равен β. То есть β=2.
Задача 24. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,75 и выборочные средние квадратические отклонения σ X =1,1 σ Y =2,2. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 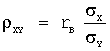
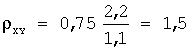
Задача 25. Мода вариационного ряда 1,2,2,3,3,3,4 равна…
Модой вариационного ряда называется варианта, имеющая наибольшую частоту. Такой вариантой является варианта 3, частота которой равна
Задача 26. Медиана вариационного ряда 3,4,5,6,7,12 равна…
Медианой вариационного ряда называется варианта, расположенная в середине вариационного ряда. Так как в середине ряда располагаются две варианты: 5 и 6, то медиана равна их средней арифметической 5,5.
Задача 27. Размах варьирования вариационного ряда 3,5,5,7,9,10,16 равен…
Размах варьирования вариационного ряда определяется как R = xmax — xmin , то есть R =16-3=13.
Задача 28. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 10, 12. Тогда несмещенная оценка дисперсии равна…
Несмещенная оценка дисперсии вычисляется по формуле: 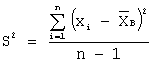
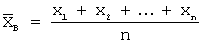
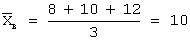

Задача 29. Из генеральной совокупности извлечена выборка объема n =20:
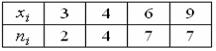
Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 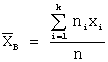
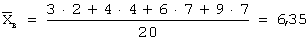
Задача 30. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 11, 13, 14. Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 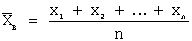

Задача 31. Дана интервальная оценка (8,45;9,15) математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна…
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна 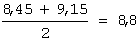
Задача 32. Дана интервальная оценка (10,45;11,55) математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна…
Точность интервальной оценки ( a ; b ) определяется как 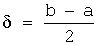
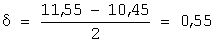
Задача 33. Из генеральной совокупности извлечена выборка объема n =50, гистограмма частот которой имеет вид:
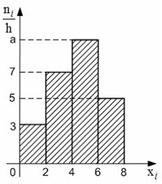
Тогда значение a равно…
Так как объем выборки вычисляется как n =( a +7+5+3) h , то a =50/2-7-5-3=10.
- Решения задач: линейная регрессия и коэффициент корреляции
- Примеры решений онлайн: линейная регрессия
- Простая выборка
- Корреляционная таблица
- Коэффициент корреляции
- Практическое задание Эконометрика. Группа Вл19Э291 Студент москва 2022 Вопросы Укажите основные этапы эконометрического исследования
- Группа Вл19Э291
- 📹 Видео
Видео:Математика #1 | Корреляция и регрессияСкачать

Решения задач: линейная регрессия и коэффициент корреляции
Парная линейная регрессия — это зависимость между одной переменной и средним значением другой переменной. Чаще всего модель записывается как $y=ax+b+e$, где $x$ — факторная переменная, $y$ — результативная (зависимая), $e$ — случайная компонента (остаток, отклонение).
В учебных задачах по математической статистике обычно используется следующий алгоритм для нахождения уравнения регрессии.
- Выбор модели (уравнения). Часто модель задана заранее (найти линейную регрессию) или для подбора используют графический метод: строят диаграмму рассеяния и анализируют ее форму.
- Вычисление коэффициентов (параметров) уравнения регрессии. Часто для этого используют метод наименьших квадратов.
- Проверка значимости коэффициента корреляции и параметров модели (также для них можно построить доверительные интервалы), оценка качества модели по критерию Фишера.
- Анализ остатков, вычисление стандартной ошибки регрессии, прогноз по модели (опционально).
Ниже вы найдете решения для парной регрессии (по рядам данных или корреляционной таблице, с разными дополнительными заданиями) и пару задач на определение и исследование коэффициента корреляции.
Видео:Коэффициент корреляции Пирсона в ExcelСкачать

Примеры решений онлайн: линейная регрессия
Простая выборка
Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.
Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.
Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.
Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью.
Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.
Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
Корреляционная таблица
Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице
Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.
Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.
Коэффициент корреляции
Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?
Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $overline=82$ у.е., $S_x=31$ у.е., $overline=39$ у.е., $S_y=29$ у.е., $overline =3709$ (у.е.)2. При $alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.
Видео:Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Практическое задание Эконометрика. Группа Вл19Э291 Студент москва 2022 Вопросы Укажите основные этапы эконометрического исследования
| Название | Группа Вл19Э291 Студент москва 2022 Вопросы Укажите основные этапы эконометрического исследования |
| Анкор | Практическое задание Эконометрика |
| Дата | 09.01.2022 |
| Размер | 57.58 Kb. |
| Формат файла |  |
| Имя файла | Практическое задание Эконометрика.docx |
| Тип | Документы #326405 |
 С этим файлом связано 8 файл(ов). Среди них: Пример оформления КП.pdf, 1954849191290720-19.doc, Курсач.docx, История эк учений.docx, Практические задания Налогообложение.docx, Практические задания БК.docx, Практические задания БФУ Жданова ВС.docx, Практическое задание Документооборот.docx. С этим файлом связано 8 файл(ов). Среди них: Пример оформления КП.pdf, 1954849191290720-19.doc, Курсач.docx, История эк учений.docx, Практические задания Налогообложение.docx, Практические задания БК.docx, Практические задания БФУ Жданова ВС.docx, Практическое задание Документооборот.docx.  Показать все связанные файлы Подборка по базе: график отпусков касса рег 2022 дұрысы (2) (2).docx, собственный капитал коммерческого банка, 2022.doc, ЕГЭ. 2022. Открытый пробный 2. 4 ЕГЭ портал. Ответы.pdf, ЕГЭ. 2022. Открытый пробный 3. 4 ЕГЭ портал.docx, ЕГЭ. 2022. Открытый пробный 2. 4 ЕГЭ портал.docx, Сочинение 2022.docx, ЕГЭ. 2022. Открытый пробный 1. 4 ЕГЭ портал.docx, Практическая работа 5. курсы 2022.docx, Демо 2022 матем (1).docx, Реферат по истории Студентовой Ирины (2).docx Показать все связанные файлы Подборка по базе: график отпусков касса рег 2022 дұрысы (2) (2).docx, собственный капитал коммерческого банка, 2022.doc, ЕГЭ. 2022. Открытый пробный 2. 4 ЕГЭ портал. Ответы.pdf, ЕГЭ. 2022. Открытый пробный 3. 4 ЕГЭ портал.docx, ЕГЭ. 2022. Открытый пробный 2. 4 ЕГЭ портал.docx, Сочинение 2022.docx, ЕГЭ. 2022. Открытый пробный 1. 4 ЕГЭ портал.docx, Практическая работа 5. курсы 2022.docx, Демо 2022 матем (1).docx, Реферат по истории Студентовой Ирины (2).docx
«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» | |||||||||||||||||
| Кафедра экономики и управления Форма обучения: заочная Видео:Коэффициент корреляции. Статистическая значимостьСкачать  Группа Вл19Э291МОСКВА 2022
Ответ: Основные этапы эконометрического исследования: — постановка проблемы (используется экономическая теория); — подготовка информации (используется статистика); — формулировка вида моделей количественных показателей экономики и их взаимосвязей (используются экономическая теория и математика); — оценка параметров и анализ качества моделей (используются математика, и, в частности, математическая статистика); -анализ и прогнозы количественных показателей экономики с помощью «удачных», с точки зрения статистических критериев, моделей, экономическое толкование результатов (используются экономическая теория и математика).
Ответ: Наиболее часто используются линейная и степенная функции. В линейной модели параметры bi при факторах хi характеризуют величину среднего изменения зависимой переменной y с изменением соответствующего фактора хi на единицу, в то время как значения остальных факторов остаются неизмененными. В степенной модели параметры bj при факторах хi являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменяется зависимая переменная y при изменении соответствующего фактора хi на 1 % в условиях неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.
Ответ: В парной регрессии выбор вида математической функции ŷх = f(x) может быть осуществлен тремя методами: Класс математических функций для описания связи двух переменных достаточно широк. Основными являются следующие: 4. ŷх = a + b*x + c*x2; 5. ŷх = a + b*x + c*x2 + d*x3; 6. ŷх = a*bx.
Ответ: Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx. Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности. Выборочный парный коэффициент корреляции ryx: где ух – среднее арифметическое произведения факторной и результативной переменных: S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной у от ее среднего значения y–: у 2 – среднее значение из квадратов значений результативной переменной у : Выборочный коэффициент корреляции обладает следующими свойствами: 1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1; 2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным; 3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью; 4) если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
Ответ: Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. Определение тенденции развития, построение модели, описывающей изменение явления во времени, прогнозирование явления — все это важнейшие задачи при изучении динамических рядов экономических и социальных показателей. На формирование уровней динамического ряда влияет множество различных факторов, которые по характеру воздействия можно объединить в три группы:
Соответственно, для анализа закономерности изменения уровней ряда динамики во времени применяют следующую модель: где Тt — основная тенденция ряда (тренд); St — циклические (в частности, сезонные) колебания; еt — случайные колебания. В аддитивной модели ряд динамики представлен как сумма перечисленных компонент , в мультипликативной модели — как их произведение [ Тенденцией развития, или трендом, называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов. Судить о наличии тенденции в динамическом ряду на основе его визуального анализа можно лишь тогда, когда четко видно, что при переходе от одного момента времени к другому уровни ряда возрастают или убывают. Однако, как правило, нельзя сразу сказать, есть или нет тенденция в изменении уровней динамического ряда. Для этого применяются специальные методы. К методам выявления основной тенденции развития динамического ряда (Тt) относятся:
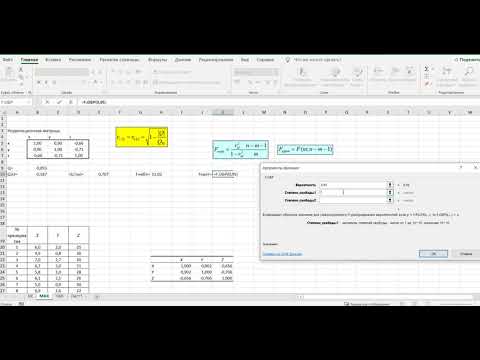
Таблица 3. Регрессионный анализ.
Система нормальных уравнений. | x | y | x 2 | y 2 | x*y | ||||||||||||
| 10 | 7,38 | 100 | 54,4644 | 73,8 | |||||||||||||
| 20 | 18,15 | 400 | 329,4225 | 363 | |||||||||||||
| 30 | 44,64 | 900 | 1992,7296 | 1339,2 | |||||||||||||
| 40 | 109,79 | 1600 | 12053,8441 | 4391,6 | |||||||||||||
| 50 | 270,06 | 2500 | 72932,4036 | 13503 | |||||||||||||
| ∑ | 150 | 450,02 | 5500 | 87362,8642 | 19670,6 |
Для наших данных система уравнений имеет вид














Найдём 




Степенная зависимость




Найдём 




Логарифмическая зависимость












Найдем 




- Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
Таблица 4. Корреляционный анализ.
| Значения вел X № варианта | 10 | 20 | 30 | 40 | 50 |
| 1 | 7,38 | 18,15 | 44,64 | 109,79 | 270,06 |
Решение:
Для расчёта параметров регрессии построим расчётную таблицу

Рассчитываем количественное значение коэффициента парной линейной корреляции по формуле:
📹 Видео
Коэффициент корреляции ПирсонаСкачать

Парная регрессия: линейная зависимостьСкачать

Коэффициент корреляции Пирсона, 2 способа вычисленияСкачать

Расчет коэффициента корреляции в ExcelСкачать

Коэффициент корреляции ПирсонаСкачать

Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Эконометрика. Линейная парная регрессияСкачать

Множественный и частные коэффициенты корреляцииСкачать
Множественный и частные коэффициенты корреляцииСкачать

Парная нелинейная регрессияСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать

Видеоурок: Расчет коэффициента корреляцииСкачать

Коэффициент корреляции ПирсонаСкачать

КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12Скачать



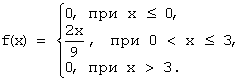






 ]. В дальнейшем будем исходить из предположения мультипликативной формы связи между компонентами ряда динамики.
]. В дальнейшем будем исходить из предположения мультипликативной формы связи между компонентами ряда динамики.








