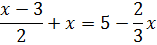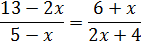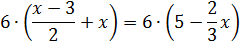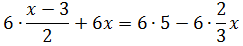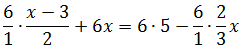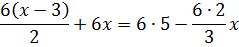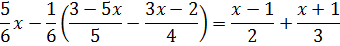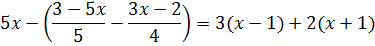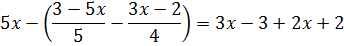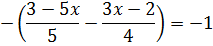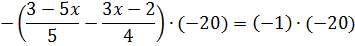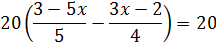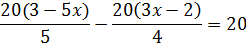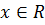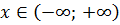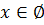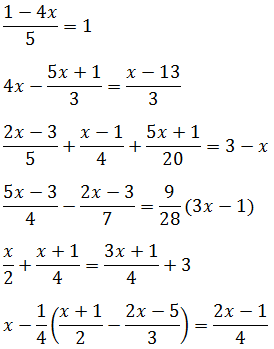При переносе дроби в другую часть уравнения знаки меняются (2 видео)

Линейные уравнения. Решение линейных уравнений. Правило переноса слагаемого.

Правило переноса слагаемого.

При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения. Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус». Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный. Кроме того, правило работает и для неравенств.

Примеры переноса слагаемого:

Сначала переносим 5x из левой части уравнения в правую:

Далее переносим (−6) из правой части в левую:

Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+». При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение.

Переносим 1-е слагаемое в правую сторону уравнения. Получаем:

Обратите внимание, что в нашем примере слагаемое — это выражение (−3x 2 (2+7x)). Поэтому нельзя отдельно переносить (−3x 2 ) и (2+7x), так как это составляющие слагаемого. Именно поэтому не переносят (−3x 2 ⋅2) и (7x). Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга.

Таким же образом преобразовывают неравенства:

Собираем каждое число с одной стороны. Получаем:

2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону. Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-».

Это правило зачастую используется для решения линейных уравнений. Для решения систем линейных уравнений используются другие методы.

Содержание

Как решать линейные уравнения?
Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?
Три в пятой степени плюс три в девятой степени — числителе, в знаменателе — три в минус пятой степени плюс три в минус девятой степени?
2)Обе части уравнения разделили на одно и тоже число, отличное от нуля?
Где поставить знаки плюс и минус между числами я уже запуталась 1234567 = 40?
Если в верху дроби минус а внизу плюс после перевода дроби в десятичную будет минус или плюс?
Дробь В числителе квадратный корень из 5 минус корень квадратный из 3, в знаменателе корень квадратный из 5 плюс корень квадратный из 3?
Найдите наименьшее положительное число х, обладающее следующими свойствами : а)Х равен дроби, числитель и знаменатель которой — двузначные числа ; б)если числитель этой дроби уменьшить на единицу, а з?
Помогите пожалуйста какую часть неправильных дробей с числителем 36 составляют дроби у которых числитель и знаменатель взаимно простые числа?
Разгадай ребус?
1)Чтобы найти часть числа, выраженную дробью, надо это число?
Чтобы найти часть от числа, выраженную дробью, необходимо?
🎬 Видео

Видео:Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

Как решать линейные уравнения?

Линейные уравнения — довольно безобидная и понятная тема школьной математики. Но, как это ни странно, количество ошибок на ровном месте при решении линейных уравнений лишь немногим меньше, чем в других темах — квадратных уравнениях, логарифмах, тригонометрии и прочих. Причины большинства ошибок — банальные тождественные преобразования уравнений. В первую очередь, это путаница в знаках при переносе слагаемых из одной части уравнения в другую, а также ошибки при работе с дробями и дробными коэффициентами. Да-да! Дроби в линейных уравнениях тоже встречаются! Сплошь и рядом. Чуть ниже такие злые уравнения мы с вами тоже обязательно разберём.)

Ну что, не будем тянуть кота за хвост и начнём разбираться, пожалуй? Тогда читаем и вникаем.)

Что такое линейное уравнение? Примеры.

Обычно линейное уравнение имеет следующий вид:

где a и b — любые числа. Какие угодно: целые, дробные, отрицательные, иррациональные — всякие могут быть!

7х + 1 = 0 (здесь a = 7, b = 1)

x — 3 = 0 (здесь a = 1, b = -3)

x/2 — 1,1 = 0 (здесь a = 1/2, b = -1,1)

В общем, вы поняли, я надеюсь.) Всё просто, как в сказке. До поры до времени… А если присмотреться к общей записи ax+b=0 более пристально, да немного призадуматься? Ведь a и b — любые числа! А если у нас, скажем, a = 0 и b = 0 (любые же числа можно брать!), то что у нас тогда получится?

Но и это ещё не все приколы! А если, допустим, a = 0, b = -10? Тогда уже совсем какая-то ахинея получается:

Что весьма и весьма напрягает и подрывает завоёвываемое потом и кровью доверие к математике… Особенно на контрольных и экзаменах. А ведь из этих непонятных и странных равенств ещё и икс найти нужно! Которого нету вообще! И вот тут даже хорошо подготовленные ученики, порой, могут впасть, что называется, в ступор… Но не переживайте! В данном уроке все такие сюрпризы мы тоже рассмотрим. И икс из таких равенств тоже обязательно отыщем.) Причём этот самый икс ищется очень и очень просто. Да-да! Удивительно, но факт.)

Ну хорошо, это понятно. Но как же можно узнать по внешнему виду задания, что перед нами именно линейное уравнение, а не какое-либо ещё? К сожалению, только по внешнему виду распознать тип уравнения возможно далеко не всегда. Дело всё в том, что линейными называются не только уравнения вида ax+b=0, но и любые другие уравнения, которые тождественными преобразованиями, так или иначе, сводятся к такому виду. А как тут узнаешь, сводится оно или нет? Пока пример почти не решишь — почти никак. Это огорчает. Но для некоторых типов уравнений можно при одном беглом взгляде сразу с уверенностью сказать, линейное оно или нет.

Для этого ещё разок обратимся к общей структуре любого линейного уравнения:

Обратите внимание: в линейном уравнении всегда присутствует только переменная икс в первой степени и какие-то числа! И всё! Больше ничего. При этом нету иксов в квадрате, в кубе, под корнем, под логарифмом и прочей экзотики. И (что особенно важно!) нет дробей с иксом в знаменателях! А вот дроби с числами в знаменателях или деление на число — запросто!

Это линейное уравнение. В уравнении присутствуют только иксы в первой степени да числа. И нету иксов в более высоких степенях — в квадрате, в кубе и так далее. Да, здесь есть дроби, но при этом в знаменателях дробей сидят только числа. А именно — двойка и тройка. Иными словами, в уравнении нету деления на икс.

А вот уравнение

уже нельзя назвать линейным, хотя здесь тоже присутствуют только числа и иксы в первой степени. Ибо, помимо всего прочего, здесь есть ещё и дроби с иксами в знаменателях. И после упрощений и преобразований такое уравнение может стать каким угодно: и линейным, и квадратным — всяким.

Как решать линейные уравнения? Примеры.

Так как же решать линейные уравнения? Читайте дальше и удивляйтесь.) Всё решение линейных уравнений базируется всего на двух основных вещах. Перечислим их.

1) Набор элементарных действий и правил математики.

Это использование скобок, раскрытие скобок, работа с дробями, работа с отрицательными числами, таблица умножения и так далее. Эти знания и умения необходимы не только для решения линейных уравнений, а для всей математики вообще. И, если с этим проблемы, вспоминайте младшие классы. Иначе несладко вам придётся…

Их всего два. Да-да! Более того, эти самые базовые тождественные преобразования лежат в основе решения не только линейных, а вообще любых уравнений математики! Одним словом, решение любого другого уравнения — квадратного, логарифмического, тригонометрического, иррационального и т.д. — как правило, начинается с этих самых базовых преобразований. А вот решение именно линейных уравнений, собственно, на них же (преобразованиях) и заканчивается. Готовым ответом.) Так что не поленитесь и прогуляетесь по ссылке.) Тем более, что там линейные уравнения тоже детально разбираются.

Что ж, я думаю, пора приступать к разбору примеров.

Для начала, в качестве разминки, рассмотрим какую-нибудь элементарщину. Безо всяких дробей и прочих наворотов. Например, такое уравнение:

Это классическое линейное уравнение. Все иксы максимум в первой степени и деления на икс нигде нету. Схема решения в таких уравнениях всегда едина и проста до ужаса: все члены с иксами надо собрать слева, а все члены без иксов (т.е. числа) собрать справа. Вот и приступаем к сбору.

Для этого запускаем в ход первое тождественное преобразование. Нам нужно перенести -5х влево, а -2 перенести вправо. Со сменой знака, ясное дело.) Вот и переносим:

Ну вот. Полдела сделано: иксы собрали в кучку, числа — тоже. Теперь слева приводим подобные, а справа — считаем. Получаем:

Чего теперь нам не хватает для полного счастья? Да чтобы слева чистый икс остался! А шестёрка — мешает. Как от неё избавиться? Запускаем теперь второе тождественное преобразование — делим обе части уравнения на 6. И — вуаля! Ответ готов.)

Разумеется, пример совсем примитивный. Чтобы общую идею уловить. Что ж, решим что-нибудь посущественнее. Например, разберём вот такое уравнение:

Детально разберём.) Это тоже линейное уравнение, хотя, казалось бы, тут есть дроби. Но в дробях есть деление на двойку и есть деление на тройку, а вот деления на выражение с иксом — нету! Так что — решаем. Используя всё те же тождественные преобразования, да.)

Что вначале делать будем? С иксами — влево, без иксов — вправо? В принципе, можно и так. Лететь в Сочи через Владивосток.) А можно пойти по кратчайшему пути, сразу воспользовавшись универсальным и мощным способом. Если знать тождественные преобразования, разумеется.)

Для начала задаю ключевой вопрос: что вам сильнее всего бросается в глаза и больше всего не нравится в этом уравнении? 99 человек из 100 скажут: дроби! И будут правы.) Вот и избавимся сначала от них. Безопасно для самого уравнения.) Поэтому начнём сразу со второго тождественного преобразования — с домножения. На что надо помножить левую часть, чтобы знаменатель благополучно сократился? Правильно, на двойку. А правую часть? На тройку! Но… Математика — дама капризная. Она, понимаешь, требует умножать обе части только на одно и то же число! Каждую часть помножать на своё число — не катит… Что делать будем? Что-что… Искать компромисс. Чтобы и наши хотелки удовлетворить (избавиться от дробей) и математику не обидеть.) А помножим-ка обе части на шестёрку!) То есть, на общий знаменатель всех дробей, входящих в уравнение. Тогда одним махом и двойка сократится, и тройка!)

Вот и домножаем. Всю левую часть и всю правую часть целиком! Посему используем скобочки. Вот так выглядит сама процедура:

Теперь раскрываем эти самые скобочки:

Теперь, представив 6 как 6/1, помножим шестёрку на каждую из дробей слева и справа. Это обычное умножение дробей, но, так уж и быть, распишу детально:

А вот здесь — внимание! Числитель (х-3) я взял в скобки! Это всё потому, что при умножении дробей числитель умножается весь, целиком и полностью! И с выражением х-3 надо работать как с одной цельной конструкцией. А вот если вы запишете числитель вот так:

то это будет ошибкой. Дальше можно уже не решать, да…

Но у нас всё правильно и надо дорешивать. Что дальше делать? Раскрывать скобки в числителе слева? Ни в коем случае! Мы с вами домножали обе части на 6, чтобы от дробей избавиться, а не для того чтобы париться с раскрытием скобок. На данном этапе нам надо сократить наши дроби. С чувством глубокого удовлетворения сокращаем все знаменатели и получаем уравнение безо всяких дробей, в линеечку:

А вот теперь и оставшиеся скобки можно раскрыть:

3х — 9 + 6х = 30 — 4х

Уравнение становится всё лучше и лучше! Вот теперь вновь вспоминаем про первое тождественное преобразование. С каменным лицом повторяем заклинание из младших классов: с иксами — влево, без иксов — вправо. И применяем это преобразование:

3х + 6х + 4х = 30 + 9

Приводим подобные слева и считаем справа:

Осталось поделить обе части на 13. То есть, вновь применить второе преобразование. Делим и получаем ответ:

Готово дело. Как вы видите, в данном уравнении нам пришлось один раз применить первое преобразование (перенос слагаемых) и дважды — второе: в начале решения мы использовали домножение (на 6) с целью избавиться от дробей, а в конце решения использовали деление (на 13), чтобы избавиться от коэффициента перед иксом. И решение любого (да-да, любого!) линейного уравнения состоит из комбинации этих самых преобразований в той или иной последовательности. С чего именно начинать — от конкретного уравнения зависит. Где-то выгоднее начинать с переноса, а где-то (как в этом примере) — с домножения (или деления).

Работаем от простого — к сложному. Рассмотрим теперь откровенную жесть. С кучей дробей и скобок. А я уж подскажу, как не надорваться.)

Например, вот такое уравнение:

Минуту смотрим на уравнение, ужасаемся, но всё-таки берём себя в руки! Основная проблема — с чего начинать? Можно сложить дроби в правой части. Можно выполнить вычитание дробей в скобках. Можно обе части на что-нибудь домножить. Или поделить… Так что же всё-таки можно? Ответ: всё можно! Ни одно из перечисленных действий математика не запрещает. И какую бы последовательность действий и преобразований вы бы ни выбрали, ответ получится всегда один — правильный. Если, конечно, на каком-то шаге не нарушить тождественность ваших преобразований и, тем самым, не наляпать ошибок…

А, чтобы не наляпать ошибок, в таких навороченных примерах, как этот, всегда полезнее всего оценить его внешний вид и в уме прикинуть: что можно такое сделать в примере, чтобы максимально упростить его за один шаг?

Вот и прикидываем. Слева стоят шестёрки в знаменателях. Лично мне они не нравятся, а убрать их очень легко. Домножу-ка я обе части уравнения на 6! Тогда шестёрки слева благополучно сократятся, дроби в скобках пока никуда не денутся. Ну и ничего страшного. С ними чуток позже расправимся.) А вот справа у нас сократятся знаменатели 2 и 3. Именно при этом действии (умножении на 6) у нас за один шаг достигаются максимальные упрощения!

После умножения всё наше злое уравнение станет вот таким:

Кто не понял, как именно получилось это уравнение, значит, вы плохо усвоили разбор предыдущего примера. А я старался, между прочим…

Что дальше можно сделать? Дальше удобнее всего раскрыть все скобки справа. Причём правильно раскрыть, соблюдая основы! В правой части перед обеими скобками стоит знак плюс, поэтому все знаки при раскрытии сохраняются.

Теперь самым логичным шагом было бы уединить дроби слева, а 5х отправить в правую часть. Заодно и подобные в правой части приведём. Получим:

Уже гораздо лучше. Теперь левая часть сама собой подготовилась к умножению. На что надо домножить левую часть, чтобы сразу и пятёрка сократилась, и четвёрка? На 20! Но ещё у нас присутствуют минусы в обеих частях уравнения. Поэтому удобнее всего будет умножать обе части уравнения не на 20, а на -20. Тогда одним махом и минусы исчезнут, и дроби.

Кому до сих пор непонятен этот шаг — значит, проблемы не в уравнениях. Проблемы — в основах! Вновь вспоминаем золотое правило раскрытия скобок:

Если число умножается на какое-то выражение в скобках, то это число надо последовательно умножить на каждое слагаемое этого самого выражения. При этом если число положительно, то знаки выражений после раскрытия сохраняются. Если отрицательно — меняются на противоположные:

a(b+c) = ab+ac

-a(b+c) = -ab-ac

Минусы у нас исчезли после домножения обеих частей на -20. И теперь скобки с дробями слева мы умножаем на вполне себе положительное число 20. Стало быть, при раскрытии этих скобок все знаки, что были внутри них, сохраняются. А вот откуда взялись скобки в числителях дробей, я уже подробно объяснял в предыдущем примере.

А вот теперь дроби и сократить можно:

Раскрываем оставшиеся скобки. Опять же, правильно раскрываем. Первые скобки умножаются на положительное число 4 и, стало быть, все знаки при их раскрытии сохраняются. А вот вторые скобки умножаются на отрицательное число -5 и, поэтому, все знаки меняются на противоположные:

12 — 20х — 15х + 10 = 20

Остались сущие пустяки. С иксами влево, без иксов — вправо:

-20х — 15х = 20 — 10 — 12

Вот почти и всё. Слева нужен чистый икс, а число -35 мешает. Вот и делим обе части на (-35). Напоминаю, что второе тождественное преобразование разрешает нам умножать и делить обе части на какое угодно число. В том числе и на отрицательное.) Лишь бы не на ноль! Смело делим и получаем ответ:

На сей раз икс получился дробным. Ничего страшного. Такой уж пример.)

Как мы видим, принцип решения линейных уравнений (даже самых накрученных) довольно простой: берём исходное уравнение и тождественными преобразованиями последовательно упрощаем его прямо до получения ответа. С соблюдением основ, разумеется! Главные проблемы здесь именно в несоблюдении основ (скажем, перед скобками стоит минус, а знаки при раскрытии поменять забыли), а также в банальной арифметике. Так что не пренебрегайте основами! Они — фундамент всей остальной математики!

Некоторые приколы при решении линейных уравнений. Или особые случаи.

Всё бы ничего. Однако… Попадаются среди линейных уравнений и такие забавные перлы, которые в процессе их решения могут и в сильный ступор вогнать. Даже отличника.)

Например, вот такое безобидное с виду уравнение:

7х + 3 = 4х + 5 + 3х — 2

Широко позёвывая и слегка скучая, собираем все иксы слева, а все числа справа:

Приводим подобные, считаем и получаем:

Вот-те раз! Выдал примерчик фокус! Само по себе это равенство возражений не вызывает: ноль действительно равен нулю. Но икс-то пропал! Бесследно! А мы обязаны записать в ответе, чему равен икс. Иначе решение не считается, да.) Что же делать?

Без паники! В таких нестандартных случаях спасают самые общие понятия и принципы математики. Что такое уравнение? Как решать уравнения? Что значит решить уравнение?

Решить уравнение — это значит, найти все значения переменной икс, которые при подстановке в исходное уравнение дадут нам верное равенство (тождество)!

Но верное равенство у нас уже получилось! 0=0, вернее некуда!) Остаётся догадаться, при каких именно иксах у нас получается это равенство. Какие же такие иксы можно подставлять в исходное уравнение, если при подстановке все они всё равно посокращаются в полный ноль? Неужели ещё не догадались?

Ну, конечно же! Иксы можно подставлять любые. Совершенно любые. Какие хотите, такие и подставляйте. Хоть 1, хоть -23, хоть 2,7 — какие угодно! Они всё равно сократятся и в результате останется чистая правда. Попробуйте, поподставляйте и убедитесь лично.)

Вот вам и ответ:

В научной записи это равенство пишется так:

Читается эта запись так: «Икс — любое действительное число.»

Или в другой форме, через промежутки:

Как вам больше нравится, так и оформляйте. Это верный и совершенно полноценный ответ!

А теперь я изменю в нашем исходном уравнении всего одно число. Вот такое уравнение теперь решим:

7х + 2 = 4х + 5 + 3х — 2

Опять переносим слагаемые, считаем и получаем:

7х — 4х — 3х = 5 — 2 — 2

И как вам этот прикол? Было обычное линейное уравнение, а стало непонятное равенство

Говоря научным языком, мы получили неверное равенство. А по-русски неправда это. Бред сивой кобылы. Ахинея.) Ибо ноль никак не равен единице!

А теперь опять соображаем, какие же иксы при подстановке в исходное уравнение дадут нам верное равенство? Какие? А никакие! Какой икс ни подставляй, всё равно всё посокращается и останется лажа.)

Вот и ответ: решений нет.

В математической записи такой ответ оформляется вот так:

Читается: «Икс принадлежит пустому множеству.»

Такие ответы в математике тоже встречаются довольно часто: далеко не всегда у какого-либо уравнения имеются корни в принципе. Какие-то уравнения могут и вовсе не иметь корней. Совсем.

Вот такие вот два сюрприза. Надеюсь, что теперь внезапная пропажа иксов в уравнении не поставит вас навечно в тупик. Дело вполне знакомое.)

И тут слышу закономерный вопрос: а в ОГЭ или ЕГЭ они будут? На ЕГЭ сами по себе в качестве задания — нет. Слишком уж простенькие. А вот в ОГЭ или в текстовых задачках — запросто! Так что теперь — тренируемся и решаем:

Ответы (в беспорядке): -2; -1; любое число; 2; нет решений; 7/13.

Всё получилось? Отлично! У вас неплохие шансы на экзамене.

Что-то не сходится? Гм… Печалька, конечно. Значит, где-то пока есть пробелы. Либо в основах, либо в тождественных преобразованиях. Либо же дело в банальной невнимательности. Перечитайте урок ещё раз. Ибо не та это тема, без которой можно вот так легко обойтись в математике…

Удачи! Она вам обязательно улыбнётся, поверьте!)

Видео:Решение уравнений. Часть 2. 6 класс.Скачать

Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?

Математика | 5 — 9 классы

Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?

Ну вообще, по сути, если дробь такая 7 / 5, то если ее перенести в другую часть уравнения, то получится что минус надо ставить перед дробью, а не в числителе или знаменателе.

Если это так, то со сложным числителем так же, просто ставится минус перед дробью).

Видео:Почему при переносе слагаемого из одной части уравнения в другую знак меняется на противоположный?Скачать

Три в пятой степени плюс три в девятой степени — числителе, в знаменателе — три в минус пятой степени плюс три в минус девятой степени?

Три в пятой степени плюс три в девятой степени — числителе, в знаменателе — три в минус пятой степени плюс три в минус девятой степени.

Видео:Решение уравнений, 6 классСкачать

2)Обе части уравнения разделили на одно и тоже число, отличное от нуля?

2)Обе части уравнения разделили на одно и тоже число, отличное от нуля.

Изменились ли корни данного уравнения?

3)сформулируйте правило переноса слагаемых из одной части уравнения в другую.

4)какие уравнения называют линейными?

Видео:Виды уравнений. Свойства уравнений. Перенос слагаемых из одной части уравнения в другую. Алгебра 7.Скачать

Где поставить знаки плюс и минус между числами я уже запуталась 1234567 = 40?

Где поставить знаки плюс и минус между числами я уже запуталась 1234567 = 40.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Если в верху дроби минус а внизу плюс после перевода дроби в десятичную будет минус или плюс?

Видео:Почему при переносе слагаемого знак меняется?Скачать

Дробь В числителе квадратный корень из 5 минус корень квадратный из 3, в знаменателе корень квадратный из 5 плюс корень квадратный из 3?

Дробь В числителе квадратный корень из 5 минус корень квадратный из 3, в знаменателе корень квадратный из 5 плюс корень квадратный из 3.

Минус дробь — в числителе корень квадратный из 5 плюс корень квадратный из 3, в знаменателе корень квадратный из 5 минус корень квадратный из 3.

Видео:Вся суть уравнений за 1 секунду. Хватит путать знаки в уравнениях!Скачать

Найдите наименьшее положительное число х, обладающее следующими свойствами : а)Х равен дроби, числитель и знаменатель которой — двузначные числа ; б)если числитель этой дроби уменьшить на единицу, а з?

Найдите наименьшее положительное число х, обладающее следующими свойствами : а)Х равен дроби, числитель и знаменатель которой — двузначные числа ; б)если числитель этой дроби уменьшить на единицу, а знаменатель удвоить, то дробь станет равной 1 / 11 ; В ответе укажите сумму числителя и знаменателя полученной дроби Х без пробелов и каких — либо знаков препинания, например 100.

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Помогите пожалуйста какую часть неправильных дробей с числителем 36 составляют дроби у которых числитель и знаменатель взаимно простые числа?

Помогите пожалуйста какую часть неправильных дробей с числителем 36 составляют дроби у которых числитель и знаменатель взаимно простые числа.

Видео:Как решать уравнения с дробью? #shortsСкачать

Разгадай ребус?

Установите соответствие между загаданным словами его значением.

А) показывает, какую часть одно число составляет от другого.

Буду) показывает, из скольких равных частей состоит дробь.

В) показывает, на сколько равных частей разделена единица.

Где) показывает, из скольких частей состоит дробь.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

1)Чтобы найти часть числа, выраженную дробью, надо это число?

1)Чтобы найти часть числа, выраженную дробью, надо это число.

На знаменатель дроби и .

2)Чтобы найти число по его части, выраженной дробью, надо эту часть .

На числитель дроби и .

3)Чтобы найти, какую часть одно число составляет от другого, надо первое число .

Видео:Решение линейных уравненийСкачать

Чтобы найти часть от числа, выраженную дробью, необходимо?

Чтобы найти часть от числа, выраженную дробью, необходимо.

1)Это число разделить на знаменатель и умножить на числитель дроби

2)Это число разделить на числитель дроби и умножить на знаменатель

3)надо одно число разделить на другое

еще мы проценты проходим в 4 классе а вы?

Вы перешли к вопросу Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.