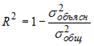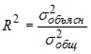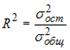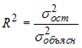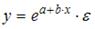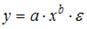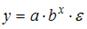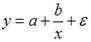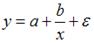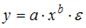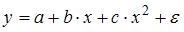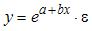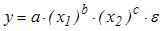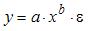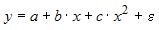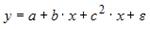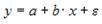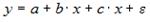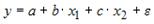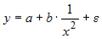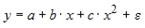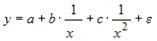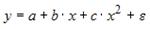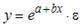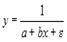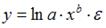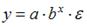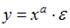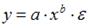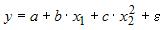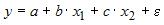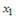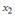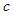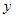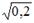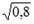Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.
Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
| 9 |
| 13 |
| 16 |
| 14 |
| 21 |
Транспонируем матрицу X, получаем X T :
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, X T X = |
|
В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
| Умножаем матрицы, X T Y = |
|
Находим обратную матрицу (X T X) -1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
| (X T X) -1 X T Y = y(x) = |
| * |
| = |
|
Получили оценку уравнения регрессии: Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 e/∑(yi — yср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .
Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),
После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица X T
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (X T X)
Умножаем матрицы, (X T Y)
Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1
Уравнение регрессии
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1
| k(x) = 0.36 |
| = |
|
Дисперсии параметров модели определяются соотношением S 2 i = Kii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
- Построение парной регрессионной модели
- V7: Система линейных одновременных уравнений
- Множественная линейная регрессия. Улучшение модели регрессии
- Понятие множественной линейной регрессии
- Уравнение множественной линейной регрессии и метод наименьших квадратов
- МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
- МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
- Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
- Оценка качества модели множественной линейной регрессии в целом
- Анализ значимости коэффициентов модели множественной линейной регрессии
- Исключение резко выделяющихся наблюдений
- Исключение незначимых переменных из модели
- Нелинейные модели для сравнения
- Применение пошаговых алгоритмов включения и исключения переменных
- Выбор самой качественной модели множественной линейной регрессии
- 📹 Видео
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Построение парной регрессионной модели
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
.
- Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам
.
- Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации 
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.
Видео:Множественная регрессия в ExcelСкачать

V7: Система линейных одновременных уравнений
S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами
-: состоятельности, смещенности и эффективности
+: состоятельности, несмещенности и эффективности
-: состоятельности, смещенности и неэффективности
-: несостоятельности, смещенности и эффективности
S: Для регрессионной модели вида 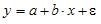
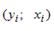
S: Для обнаружения автокорреляции в остатках используется
+: статистика Дарбина – Уотсона
-: критерий Гольдфельда – Квандта
S: Величина 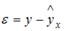
S: Строится эконометрическая модель линейного уравнения множественной регрессии вида
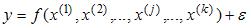
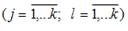
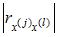
S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение
S: В эконометрической модели линейного уравнения регрессии
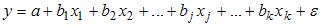
S: Система эконометрических уравнений включает совокупность _________ переменных.
S: Несмещенность оценок параметров регрессии означает, что …
-: дисперсия остатков минимальная
-: точность оценок выборки увеличивается с увеличением объема выборки
+: математическое ожидание остатков равно нулю
-: дисперсия остатков не зависит от величины
S: Дана автокорреляционная функция временного ряда
Верным будет утверждение, что ряд …
-: содержит только тенденцию, и не содержит сезонной компоненты
-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту
+: имеет выраженную сезонную компоненту с лагом 4
-: имеет выраженную сезонную компоненту с лагом 6
S: Если параметр эконометрической модели является статистически значимым, то его значение признается …
+: равным коэффициенту парной корреляции
S: Для регрессионной модели вида 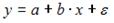
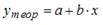
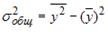
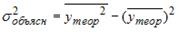
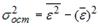
-:
+:
-:
-:
S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 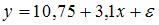
S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
-:
-:
-:
+:
S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …
-: принадлежность тому или иному региону
-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье
+: площадь жилья (м2)
S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
+:
-:
-:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
-:
-:
-:
+:
S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 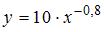
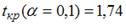
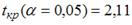
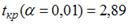
-: при уровне значимости 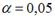
-: при уровне значимости 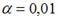
-: эластичность спроса по цене составляет –0,8
+: при уровне значимости 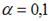
S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.
-: стохастические и вероятностные
-: линейные и парные
-: множественные и парные
+: линейные и нелинейные
S: Дана таблица исходных данных для построения эконометрической регрессионной модели:
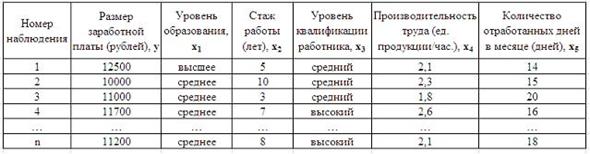
Фиктивными переменными не являются …
-: уровень квалификации работника
S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …
-: коэффициента множественной корреляции
-: показателей существенности параметров модели
+: матрицы парных коэффициентов линейной корреляции
-: системы нормальных уравнений МНК
S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 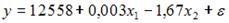
-: увеличится на 1,67
-: изменится на (-1,67)
-: изменится на 0,003
+: уменьшится на (-1,67)
S: В модели вида 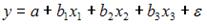
S: В модели множественной регрессии 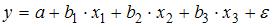
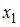
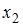
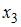
S: В уравнении линейной множественной регрессии: 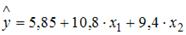
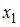
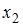
-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.
-: на 1% … увеличится на 10,8%
-: на 1 тыс. руб. … увеличится на 10,8%
+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
S: Переменная х является нелинейной в уравнении
-:
-:
+:
-:
S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является
-:
-:
+:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 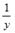
-:
-:
-:
+:
S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 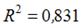
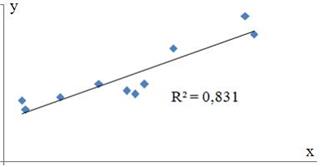
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.
S: Пусть 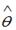

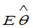
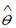
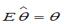
S: Степенной модельюне является регрессионная модель …
-:
+:
-:
-:
S: Нелинейным уравнением множественной регрессии является …
+:
-:
-:
-:
S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
+: бесконечно большого количества
S: В эконометрической модели линейного уравнения регрессии 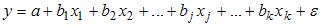
+:
S: Для эконометрической модели линейного уравнения множественной регрессии вида 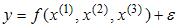

Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
S: Регрессионная модель вида 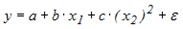
-: переменной
+: переменной
-: параметра
-: переменной
S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет
-:
-:
S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.
-: гомоскедастичными и некоррелированными
+: автокоррелированными и/или гетероскедастичными
S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
S: Автокорреляцией уровней ряда называется корреляционная зависимость между …
-: факторами, формирующими уровень ряда
-: уровнями двух рядов
+: последовательными уровнями ряда
-: компонентами, образующими уровни ряда
S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 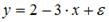
S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 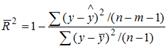
+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
-: n – число параметров при независимых переменных; m – число наблюдений
-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
S: Для эконометрической модели вида 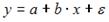

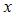
S: Ошибкой спецификации эконометрической модели уравнения регрессии является …
+: использование парной регрессии вместо множественной
-: расчет показателей качества модели
-: учет случайных факторов
-: оценка параметров при помощи МНК
S: В модели множественной регрессии 
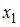
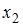
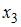
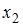
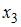
S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
-: между трендовой, сезонной и случайной компонентами
+: первого, второго, третьего и последующих порядков
-: факторов, формирующих уровень ряда
-: между несколькими временными рядами
S: Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …
-: yt = 7; T = 6,5; S = 0; E = 0,5
-: yt = 7; T = -3,5; S = -2; E = -1
+: yt = 7; T = 3,5; S = 2; E = 1
-: yt = 7; T = 3,5; S = -2; E = 1
Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Множественная линейная регрессия. Улучшение модели регрессии
Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Понятие множественной линейной регрессии
Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

где 

Функция множественной линейной регрессии для выборки имеет следующий вид:

где 

Видео:Эконометрика. Линейная парная регрессияСкачать

Уравнение множественной линейной регрессии и метод наименьших квадратов
Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.
Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.
МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений
Решение системы можно получить, например, методом Крамера:

Определитель системы записывается так:
МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:
Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

где 


Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.
Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.
Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации 

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
- условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
- условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
- условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
- условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является
Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.
В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.
В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.
Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).
Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.
Видео:Множественная регрессияСкачать

Оценка качества модели множественной линейной регрессии в целом
Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:
и следующие показатели качества описываемой этим уравнением модели:
 | adj. | RSS | SEE | F | p-level |
| 0,426 | 0,279 | 2,835 | 1,684 | 2,892 | 0,008 |
Сделать вывод о качестве модели в целом.
Ответ. По всем показателям модель некачественная. Значение 

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):
Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.
Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Анализ значимости коэффициентов модели множественной линейной регрессии
С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.
Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
| Перем. | Знач. коэф. | t | p-level |
| X1 | 0,129 | 2,386 | 0,022 |
| X2 | -0,286 | -2,439 | 0,019 |
| X3 | -0,037 | -0,238 | 0,813 |
| X4 | 0,15 | 1,928 | 0,061 |
| X5 | 0,328 | 0,548 | 0,587 |
| X6 | -0,391 | -0,503 | 0,618 |
| X7 | -0,673 | -0,898 | 0,375 |
| X8 | -0,006 | -0,07 | 0,944 |
| X9 | -1,937 | -2,794 | 0,008 |
| X10 | -1,233 | -1,863 | 0,07 |
Сделать вывод о значимости коэффициентов модели.
Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.
Видео:Множественная регрессия в программе SPSS (Multiple regression)Скачать

Исключение резко выделяющихся наблюдений
Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
| № | adj. | SEE | F | p- level | незнач. пер. |
| 10 | 0,411 | 2,55 | 2,655 | 0,015 | X3, X4, X5, X6, X7, X8, X10 |
| 3 | 0,21 | 2,58 | 2,249 | 0,036 | X3, X4, X5, X6, X7, X8, X10 |
| 4 | 0,16 | 2,61 | 1,878 | 0,082 | X3, X4, X5, X6, X7, X8, X10 |
Уравнение конечной множественной линейной регрессии:
Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.
Видео:Построение модели множественной регрессии в программе GretlСкачать

Исключение незначимых переменных из модели
Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
| Искл. пер. | adj. | SEE | F | p- level | * |
| X3 | 0,18 | 1,71 | 2,119 | 0,053 | X4, X5, X6, X7, X8, X10 |
| X4 | 0,145 | 1,745 | 1,974 | 0,077 | X5, X6, X7, X8, X10 |
| X5 | 0,163 | 2,368 | 2,282 | 0,048 | X6, X7, X8, X10 |
| X6 | 0,171 | 2,355 | 2,586 | 0,033 | X7, X8, X10 |
| X7 | 0,167 | 2,223 | 2,842 | 0,027 | X8, X10 |
| X8 | 0,184 | 1,705 | 3,599 | 0,013 | X10 |
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.
Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:
Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».
Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Нелинейные модели для сравнения
Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.
Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.
Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:
Показатели качества первой модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,17 | 0,134 | 159,9 | 1,845 | 4,8 | 0,0127 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:
Показатели качества второй модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,182 | 0,148 | 157,431 | 1,83 | 5,245 | 0 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Применение пошаговых алгоритмов включения и исключения переменных
Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
- в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
- в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
- в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).
Построить, как описано выше, модели множественной линейной регрессии автоматически.
В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
 | adj. | RSS | SEE | F | p-level |
| 0,41 | 0,343 | 113,67 | 1,61 | 6,11 | 0,002 |
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
 | adj. | RSS | SEE | F | p-level |
| 0,22 | 0,186 | 150,28 | 1,79 | 6,61 | 0 |
Видео:Эконометрика. Построение модели множественной регрессии в Excel.Скачать

Выбор самой качественной модели множественной линейной регрессии
Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
| Модель | Ручная | Кв. перем. | Лог. перем. | forward stepwise | backward stepwise |
 | 0,255 | 0,17 | 0,182 | 0,41 | 0,22 |
adj. | 0,184 | 0,134 | 0,148 | 0,343 | 0,186 |
| RSS | 122,01 | 159,9 | 157,43 | 113,67 | 150,28 |
| SEE | 1,705 | 1,845 | 1,83 | 1,61 | 1,79 |
| F | 3,599 | 4,8 | 5,245 | 6,11 | 6,61 |
| p-level | 0,013 | 0,0127 | 0 | 0,002 | 0 |
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.
📹 Видео
Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Математика #1 | Корреляция и регрессияСкачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Часть 2. Множественная регрессия в Microsoft Excel. Автокорреляция, гетероскедастичность.Скачать

EViews. Урок 1. Построение модели множественной регрессии.Скачать

09 02 Основы множественной регрессииСкачать

Пример проверки гипотезы о незначимости регрессииСкачать