- Условие
- Решение
- При каком целом значении p уравнения 3x ^ 2 — 4x + p — 2 = 0 и x ^ 2 — 2px + 5 = 0 имеют общий корень?
- Решите уравнение : способом замены переменной?
- При каких значениях а уравнение 4 + 3Х = а — 5 имеет отрицательный корень?
- Корень из 54756?
- Как решить следующую задачу : При каких значениях k имеют общий корень уравнения 7x — 2 = 0 и 3x — k = 0(Просьба решить все с объяснениями)?
- При каких значениях параметра а уравнения и будут иметь общий корень?
- При каких значениях параметра b имеют общий корень уравнения : 2x = 3b — 1 и 3x = 5b + 7?
- При каких значениях p имеют общий корень уравнения x2 + 2x + p = 0 и 3×2 + x + p — 1 = 0 ?
- Помогите решить уравнение и найти его корень?
- Найти корень уравнения : (x + 8) ^ 3 = — 64 Решите с подробностями )?
- Помогите решить пожалуйста , нужно найти корень уравнения?
- Задачи с параметром
- 📽️ Видео
Условие
При каких значениях параметра а уравнения
(1-2a)x^2-6ax-1=0 и ax^2-x+1=0
имеют общий корень?
Решение
Сумма уравнений имеет вид:
(1-a)x^2-(6a+1)x=0.
x_(1)=0 не является корнем данных уравнений.
При а=1 уравнения принимают вид
-х^2+6x-1=0
x^2-x+1=0
и не имеют общих корней.
Подставляем
х=(6а-1)/(1-а) во второе уравнение:
а*(6а-1)^2/(1-a)^2-(6a-1)/(1-a)+1=0;
a(36a^2+19a-6)=0
a_(1)=0 или
36а^2+19a-6=0
D=19^2-4*36*(-6)=361+864=1225=35^2
a_(2)=(-19-35)/72=-3/4; a_(3)=(-19+35)/72=2/9
О т в е т. при а=-3/4; а=0; а=2/9
Видео:Параметр. Общий корень квадратных уравнений.Скачать

При каком целом значении p уравнения 3x ^ 2 — 4x + p — 2 = 0 и x ^ 2 — 2px + 5 = 0 имеют общий корень?
Алгебра | 10 — 11 классы
При каком целом значении p уравнения 3x ^ 2 — 4x + p — 2 = 0 и x ^ 2 — 2px + 5 = 0 имеют общий корень?
Найти этот корень.
Помогите решить, пожалуйста, подробно.
3x² — 4x + p — 2 = x² — 2px + 5
2x² + x(2p — 4) + p — 7 = 0
D = (2p — 4)² — 8(p — 7) = 4p² — 16p + 16 — 8p + 56 = 4p² — 24p + 72≥0
D = 36 — 72 = — 36< ; 0
Видео:При каком значении параметра корни уравнения удовлетворяют условиюСкачать

Решите уравнение : способом замены переменной?
Решите уравнение : способом замены переменной.
И найти целый корень.
Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

При каких значениях а уравнение 4 + 3Х = а — 5 имеет отрицательный корень?
При каких значениях а уравнение 4 + 3Х = а — 5 имеет отрицательный корень?
Помогите пожалуйста, как можно подробнее).
Видео:11.88 найти все значения параметра а при которых два уравнения имеют общий кореньСкачать

Корень из 54756?
Корень из 54756.
Как найти, подробно, пожалуйста.
Видео:7. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРМЕТРА КОРНЕМ УРАВНЕНИЯ ЯВЛЯЕТСЯ ЛЮБОЕ ЧИСЛОСкачать

Как решить следующую задачу : При каких значениях k имеют общий корень уравнения 7x — 2 = 0 и 3x — k = 0(Просьба решить все с объяснениями)?
Как решить следующую задачу : При каких значениях k имеют общий корень уравнения 7x — 2 = 0 и 3x — k = 0(Просьба решить все с объяснениями).
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

При каких значениях параметра а уравнения и будут иметь общий корень?
При каких значениях параметра а уравнения и будут иметь общий корень?
Найдите этот корень, пожалуйста.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

При каких значениях параметра b имеют общий корень уравнения : 2x = 3b — 1 и 3x = 5b + 7?
При каких значениях параметра b имеют общий корень уравнения : 2x = 3b — 1 и 3x = 5b + 7.
Видео:При каких значениях параметра уравнение имеет единственный кореньСкачать

При каких значениях p имеют общий корень уравнения x2 + 2x + p = 0 и 3×2 + x + p — 1 = 0 ?
При каких значениях p имеют общий корень уравнения x2 + 2x + p = 0 и 3×2 + x + p — 1 = 0 ?
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Помогите решить уравнение и найти его корень?
Помогите решить уравнение и найти его корень.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Найти корень уравнения : (x + 8) ^ 3 = — 64 Решите с подробностями )?
Найти корень уравнения : (x + 8) ^ 3 = — 64 Решите с подробностями ).
Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Помогите решить пожалуйста , нужно найти корень уравнения?
Помогите решить пожалуйста , нужно найти корень уравнения.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос При каком целом значении p уравнения 3x ^ 2 — 4x + p — 2 = 0 и x ^ 2 — 2px + 5 = 0 имеют общий корень?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Задачи с параметром
1. Задача.
При каких значениях параметра a уравнение ( a — 1) x 2 + 2 x + a — 1 = 0 имеет ровно один корень?
1. Решение.
При a = 1 уравнение имеет вид 2 x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем уравнение относительно параметра a 4 a 2 — 8 a = 0, откуда a = 0 или a = 2.
1. Ответ: уравнение имеет единственный корень при a О .
2. Задача.
Найти все значения параметра a , при которых имеет два различных корня уравнение x 2 +4 ax +8 a +3 = 0.
2. Решение.
Уравнение x 2 +4 ax +8 a +3 = 0 имеет два различных корня тогда и только тогда, когда D = 16 a 2 -4(8 a +3) > 0. Получаем (после сокращения на общий множитель 4) 4 a 2 -8 a -3 > 0, откуда
| a Ц 7 2 | или a > 1 + | Ц 7 2 |
2. Ответ:
| a О (- Ґ ; 1 – | Ц 7 2 | ) И (1 + | Ц 7 2 | ; Ґ ). |
3. Задача.
Известно, что 
f 2 ( x ) = 6 x — x 2 -6.
а) Постройте график функции f 1 ( x ) при a = 1.
б) При каком значении a графики функций f 1 ( x ) и f 2 ( x ) имеют единственную общую точку?
3. Решение.
3.а. Преобразуем f 1 ( x ) следующим образом


3.б. Сразу отметим, что графики функций y = kx + b и y = ax 2 + bx + c ( a № 0) пересекаются в единственной точке тогда и только тогда, когда квадратное уравнение kx + b = ax 2 + bx + c имеет единственный корень. Используя представление f 1 из 3.а , приравняем дискриминант уравнения a = 6 x — x 2 -6 к нулю. Из уравнения 36-24-4 a = 0 получаем a = 3. Проделав то же самое с уравнением 2 x — a = 6 x — x 2 -6 найдем a = 2. Нетрудно убедиться, что эти значения параметра удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.
4. Задача.
Найти все значения a , при которых множество решений неравенства x 2 -2 ax -3 a і 0 содержит отрезок [3;6].
4. Решение.
Первая координата вершины параболы f ( x ) = x 2 -2 ax -3 a равна x 0 = a . Из свойств квадратичной функции условие f ( x ) і 0 на отрезке [3;6] равносильно совокупности трех систем
| м н о | a Ј 3, f (3) = 9-9 a і 0, | м н о | 3 a D = 4 a 2 +12 a Ј 0, | м н о | a і 6, f (6) = 36-15 a і 0. |
Решением первой системы является множество (- Ґ ,1]. Вторая и третья система решений не имеют.
4. Ответ: a О (- Ґ ,1].
5. Задача (9 кл.)
При каком наименьшем натуральном значении a уравнение
| x 2 +2 ax -3 a +7 = 2 x |
имеет ровно два решения?
5. Решение.
Перепишем это уравнение в виде x 2 + (2 a -2) x — 3 a +7 = 0. Это квадратное уравнение, оно имеет ровно два решения, если его дискриминант строго больше нуля. Вычисляя дискриминант, получаем, что условием наличия ровно двух корней является выполнение неравенства a 2 + a -6 > 0. Решая неравенство, находим a a > 2. Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим натуральным решением второго является число 3.
6. Задача (10 кл.)
Найти все значения a , при которых график функции
| f ( x ) = | x 2 + | ax +2 | a -1 |
6. Решение.
Из условия f (-1) = 1 имеем уравнение
| 1 = | 1+ | — a +2 | a -1 | , |
6. Ответ: a О [2; Ґ ).
7. Задача (10 кл.)
При каких значениях a сумма квадратов корней уравнения
| x 2 -2 ax + a 2 — a = 0 |
7. Решение.
Дискриминант уравнения x 2 -2 ax + a 2 — a = 0 равен 4 a . Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x 1 + x 2 = 2 a и x 1 · x 2 = a 2 — a . Отсюда x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 -2 x 1 · x 2 = 2 a 2 +2 a . Решениями неравенства 2 a 2 +2 a > 12, удовлетворяющими условию a і 0, являются числа a > 2.
📽️ Видео
При каком значении параметра корни квадратных уравнений не чередуются. Задание 18 (31)Скачать

8 класс. Алгебра. При каких значениях переменной имеет смысл выражениеСкачать

Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать
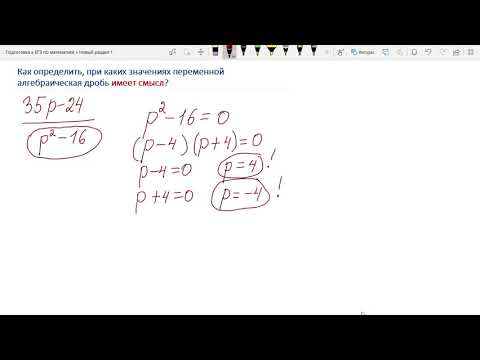
Установите при каких значениях переменной не имеет смысла алгебраическая дробьСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку?Скачать







