При каком целом значении b уравнение x 4 8x 2 b имеет три действительных корня

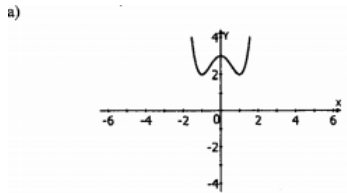
а) Постройте график функции у = х 4 — 2х 2 + 3.

б) При каких значениях параметра а уравнение х 4 — 2х 2 + 3 = а имеет три корня?

б) Количество корней в данном уравнении – это количество пересечений графиков у = х 4 – 2х 2 + 3 и у = а
Из рисунка видно, что такой случай имеет место, когда прямая у = а касается графика функции в точке (0; у(0)) у(0) = 3, следовательно, а = 3

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

При каком наименьшем значении а, уравнение х^4 — 8х^2 + 7 — а=0 имеет ровно два корня?

Это уравнение имеет ровно 4 корня. ВСЕГДА

Уравнение четвертой степени будет иметь два корня, если оно является полным квадратом. Если считать, что 8х^2 — удвоенное произведение первого,
т. е. х^2, на второе, то это «второе» равно 8/2 = 4. Тогда последнее слогаемое должно быть квадратом второго, т. е. 4^2 = 16.
Отсюда 7 — а =16, т. е. а=9.
В этом случае уравнение имеет вид (х^2 — 4)^2 = 0, и его корни х1= -2 и х2=2.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Исследование корней квадратного уравнения

Разделы: Математика

«Уравнение – это золотой ключ,
открывающий все математические сезамы»
С. Коваль

Цели урока:

• систематизирование и обобщение знаний учащихся по теме;
• развитие математического мышления;
• повышение интереса к предмету.

План урока:

1. Орг. момент
2. Устный опрос: а) работа по опроснику; б) обсуждение
3. Систематизация и обобщение знаний
4. Самостоятельная работа
5. Домашнее задание
6. Итог урока

Ход урока

1. Учитель сообщает цели и задачи урока.

Учитель: Как вы думаете, почему эпиграфом нашего урока я взяла слова С. Коваль?

2. Работа по опроснику (3 минуты) и обсуждение ответов (5 минут).

7. 3х 4 – х 2 + 16 = 0

5. х 4 – 7х 2 – 2 = 0

6. -2х 2 + 5х + 9 = 0

9. 6х 2 + 3х + 8 = 0

1. Линейные уравнения: (1, 2, 4) (№3 ?)
2. Биквадратные: (5, 7)
3. Какие уравнения имеют один корень? (1)
4. Какие уравнения не имеют корней? (2, 3, 7, 9. Почему?)
5. Какие уравнения имеют корни разного знака? (6, 8)
6. Какие уравнения имеют бесконечное множество корней? (4)
7. Какие уравнения могут иметь 4 корня? (5)

3. Учитель: Чем отличаются уравнения записанные на доске от уравнений представленные в опроснике?

x 2 – 4х + k = 0, 5nx 2 – x + 5n = 0, kx 2 + 2(k + 1)x + k + 3 = 0

Что такое параметр?

В словаре Ушакова: «ПАРАМЕТР

параметра, м. (от греч. parametreo – меряю, сопоставляя). 1. Величина, входящая в математическую формулу и сохраняющая постоянное значение в пределах одного явления или для данной частной задачи, но при переходе к другому явлению, к другой задаче меняющая свое значение (мат.).»

1. При каких значениях a уравнение 3x 2 – 6х + a = 0 имеет два положительных корня?
2. При каких значениях m уравнение x 3 – 4x 2 + mx = 0 имеет два различных корня?
3. Найти наибольшее целое значение k, при котором уравнение x 2 +x – k = 0 не имеет действительных корней?
4. Найти наименьшее целое значение a, при котором уравнение x 2 – 2 (a + 2) x = 1 2 + a 2 = 0 имеет два различных действительных корня?
5. При каком значении a уравнение ax 2 – (a + 1)x +2a – 1 = 0 имеет равные корни?

Решим уравнения № 1 и 2.

№1. 3х 2 – 6х + а = 0

1) Первое условие: два корня, следовательно, D > 0, т. е. D = 36 – 12а > 0, а 2 – 2х + a/3 =0.

3) а > 0 и а 3 – 4x 2 + mx = 0.

1) х (х 2 – 4х + m) = 0

х = 0 или х 2 – 4х + m = 0 – это уравнение должно иметь один корень, это возможно при D = 0, т.е. 16 -4m = 0, m = 4

2) Если m = 0 , то х 3 – 4х 2 = 0, х2 (х -4) = 0 – два корня.

Ответ. Уравнение имеет два корня при m = 0 и m = 4.

4. Уравнения № 3, 4, 5 решаете самостоятельно.

№3. х 2 + х – k = 0 – уравнение не имеет корней при D 2 – 2(а + 2)х + 12 + а 2 = 0 – уравнение имеет два действительных корня при D >0, т.е. 4(а + 2)2 – 4(а 2 + 12) > 0/ : 4

а 2 + 4а + 4 – а 2 – 12 > 0, 4а > 8, а > 2 – наименьшее целое значение а = 3.

Ответ. Наименьшее целое значение а = 3.

№5. ах 2 – (а + 1)х + 2а – 1 = 0 – уравнение должно иметь равные корни, следовательно, а ≠ 0, иначе уравнение обращается в линейное.

D = 0, т. е. (а + 1)2 – 4а(2а – 1) = 0 , а 2 + 2а + 1 – 8а 2 + 4а = 0,

-7а 2 + 6а + 1 =0, D = 36 + 28 = 64, а₁ = 1, а₂ = (-1/7).

Дополнительно:

№6. При каких значениях m вершины парабол y = x 2 – 4mx + m и y = -x 2 + 8mx + 4 расположены по одну сторону от оси х.

Решение. Найдем координаты вершины первой параболы y = x 2 – 4mx + m : х₀ =– = 2m, y₀ = 4m 2 – 4m*2m +m = – 4m 2 + m.

Найдем координаты вершины второй параболы y = -x 2 + 8mx + 4:

x₀ = -8m/-2 4m, y₀ = -16m 2 + 32m 2 + 4 = 16m 2 + 4, т.к. 16m 2 + 4 > 0 при любых m. Вершины парабол расположены по одну сторону от оси х, следовательно, и – 4m 2 + m > 0, m (-4m + 1) > 0. Решая методом интервалов, получим m ∊ (0; 1/4).

Ответ. При m ∊ (0; 1/4 ) вершины парабол расположены по одну сторону от оси х.

5. Домашнее задание.

6. Итог урока.

• Можно ли применять свойства корней квадратного уравнения для квадратных уравнений с параметрами?
• Как определить имеет ли уравнение с параметром корни или нет?
• Если речь идет о корнях одного знака или разного, что нужно применить для ответа на поставленный вопрос?

Урок хочется завершить словами Госсера:

Посредством уравнений, теорем
Он уйму всяких разрешил проблем:
И засуху предсказывал, и ливни –
Поистине его познанья дивны.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Уравнение х — 2 = с / х имеет два различных действительных корня, если С принадлежит множеству?

Алгебра | 10 — 11 классы

Уравнение х — 2 = с / х имеет два различных действительных корня, если С принадлежит множеству.

X — 2 = C / x, умножим левую и правую часть на x, получаем x ^ 2 — 2 * x = C, перенес С в левую часть x ^ 2 — 2 * x — C = 0.

Получаем квадратное уравнение, оно имеет два различных действительных корня если дискриминант больше 0.

D = b ^ 2 — 4 * a * c, т.

Е D = 4 — 4 * 1 * C = 4 — 4 * C,

Решаем неравенство 4 — 4 * С&gt ; 0, получаем — 4 * С&gt ; — 4, или 4 * С&lt ; 4, таким образом получаем что С&lt ; 1.

Ответ : Уравнение х — 2 = С / х имеет два действительных различных корня, если С принадлежит множеству действительных чисел и выполняется условие C&lt ; 1.

Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

При каких значениях параметра a уравнение ax² — 6x + a = 0 имеет два различных действительных корня?

При каких значениях параметра a уравнение ax² — 6x + a = 0 имеет два различных действительных корня?

Видео:Как решать такие уравнения 2^x+4^x+8^x=39Скачать

При каких значениях а уравнение ax ^ 2 + 4x — a + 5 = 0 : б)имеет два различных корня в)не имеет действительных корней?

При каких значениях а уравнение ax ^ 2 + 4x — a + 5 = 0 : б)имеет два различных корня в)не имеет действительных корней.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Сколько различных корней имеет уравнение?

Сколько различных корней имеет уравнение.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

При каком значении параметра α уравнения имеет три различных действительных корня |2x² — 5x + 3| = αЗаранее огрооооомное спасибо?

При каком значении параметра α уравнения имеет три различных действительных корня |2x² — 5x + 3| = α

Заранее огрооооомное спасибо!

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Имеет ли действительные корни уравнение : х4 — 12х2 + 36 = 0?

Имеет ли действительные корни уравнение : х4 — 12х2 + 36 = 0.

Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

При каких значениях параметра а это уравнение имеет два действительных корня?

При каких значениях параметра а это уравнение имеет два действительных корня?

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

При каких значениях параметра а уравнение (а + 2)x ^ 2 — 2(a — 1)x + a — 2 = 0 имеет два различных действительных корня?

При каких значениях параметра а уравнение (а + 2)x ^ 2 — 2(a — 1)x + a — 2 = 0 имеет два различных действительных корня.

Видео:При каких значениях x ... | ОГЭ 2017 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРАСкачать

Найдите наименьшее целое значение k, при котором уравнение x² — 2(k + 2)x + 11 + k² имеет два различных действительных корня?

Найдите наименьшее целое значение k, при котором уравнение x² — 2(k + 2)x + 11 + k² имеет два различных действительных корня.

Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

При каких значениях a уравнение (x — a)(ax ^ 2 + 6x + 5a) = 0 имеет ровно два различных действительных корня?

При каких значениях a уравнение (x — a)(ax ^ 2 + 6x + 5a) = 0 имеет ровно два различных действительных корня?

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

При каких значениях параметра p уравнение 4X ^ 2 + p = 0 имеет два различных действительных корня?

При каких значениях параметра p уравнение 4X ^ 2 + p = 0 имеет два различных действительных корня?

Вы открыли страницу вопроса Уравнение х — 2 = с / х имеет два различных действительных корня, если С принадлежит множеству?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

🎥 Видео

Как решать неравенства? Часть 1| МатематикаСкачать

№ 501-600 - Алгебра 8 класс МерзлякСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

8 класс. Алгебра. При каких значениях переменной имеет смысл выражениеСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать