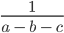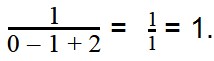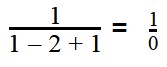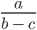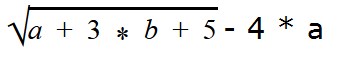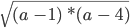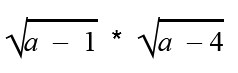При каких значениях переменной уравнение не имеет смысла 2x 8

Выражение – это самый широкий математический термин. По существу, в этой науке из них состоит все, и все операции проводятся тоже над ними. Другой вопрос, что в зависимости от конкретного вида применяются совершенно разнообразные методы и приемы. Так, работа с тригонометрией, дробями или логарифмами – это три различных действия. Выражение, не имеющее смысла, может относится к одному из двух видов: числовому или алгебраическому. А вот что означает это понятие, как выглядит его пример и прочие моменты будут рассмотрены далее.

Видео:Вариант 36, № 3. Значение переменной, при котором выражение (дробь) не имеет смысла. Пример 1Скачать

Числовые выражения

Если выражение состоит из чисел, скобок, плюсов-минусов и остальных знаков арифметических действий, его смело можно называть числовым. Что довольно логично: стоит только еще разок взглянуть на первый названный его компонент.

Числовым выражением может быть что угодно: главное, чтобы в нем не было букв. А под «чем угодно» в данном случае понимается все: от простой, стоящей одиноко, самой по себе, цифры, до огромного их перечня и знаков арифметических действий, требующих последующего вычисления конечного результата. Дробь – это тоже числовое выражение, если в ней нет всяких a, b, c, d и т.д., ведь тогда это совершенно другой вид, о котором будет рассказано чуть позже.

Видео:Как найти значения переменной, при которых алгебраическая дробь не имеет смысла?Скачать

Условия для выражения, которое не имеет смысла

Когда задание начинается со слова «вычислить», можно говорить о преобразовании. Штука в том, что это действие не всегда целесообразно: в нем не то чтобы сильно нуждаются, если на передний план выходит выражение, не имеющее смысла. Примеры бесконечно удивительны: иногда, чтобы понять, что оно-то нас и настигло, приходится долго и нудно раскрывать скобки и считать-считать-считать.

Главное, что нужно запомнить: не имеет смысла то выражения, чей конечный результат сводится к запретному в математике действию. Если уж совсем по-честному, то тогда бессмысленным становится само преобразование, но для того, чтобы это выяснить, приходится его для начала выполнить. Такой вот парадокс!

Самое знаменитое, но от того не менее важное запретное математическое действие – это деление на ноль.

Потому вот, например, выражение, не имеющее смысла:

Если при помощи нехитрых вычислений свести вторую скобку к одной цифре, то она и будет нулем.

По такому же принципу «почетное звание» дается и этому выражению:

Видео:Установите при каких значениях переменной не имеет смысла алгебраическая дробьСкачать

Алгебраические выражения

Это то же самое числовое выражение, если в него добавить запретные буквы. Тогда оно и становится полноценным алгебраическим. Оно также может быть всех размеров и форм. Алгебраическое выражение – понятие более широкое, включающее в себя предыдущее. Но был смысл начинать разговор не с него, а с числового, чтобы было понятнее и разобраться было легче. Ведь имеет ли смысл выражение алгебраическое – вопрос не то чтобы очень сложный, но имеющий больше уточнений.

Видео:Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать

Почему так?

Буквенное выражение, или выражение с переменными – это синонимы. Первый термин объяснить просто: ведь оно, в конце концов, содержит в себе буквы! Второй тоже не загадка века: вместо букв можно подставлять разные числа, вследствие чего значение выражения будет меняться. Нетрудно догадаться, что буквы в данном случае и есть переменные. По аналогии, числа – это постоянные.

И тут мы возвращаемся к основной тематике: что такое выражение, не имеющее смысла?

Видео:Задача №39. Алгебра 7 класс Макарычев.Скачать

Примеры алгебраических выражений, не имеющих смысла

Условие для бессмысленности алгебраического выражения — аналогичное, как и для числового, с одним лишь только исключением, а если быть точнее, дополнением. При преобразовании и вычислении конечного результата приходится учитывать переменные, поэтому вопрос ставится не как «какое выражение не имеет смысла?», а «при каком значении переменной это выражение не будет иметь смысла?» и «есть ли такое значение переменной, при котором выражение потеряет смысл?»

Вышеприведенное выражение не имеет смысла при a равном -2.

А вот насчет (a+3):(12-4-8) можно смело сказать, что это выражение, не имеющее смысла при любых a.

Точно так же, какое b ни подставишь в выражение (b — 11):(12+1), оно по-прежнему будет иметь смысл.

Видео:8 класс. Алгебра. При каких значениях переменной имеет смысл выражениеСкачать

Типовые задачи по теме «Выражение, не имеющее смысла»

7 класс изучает эту тему по математике в числе прочих, и задания по ней встречаются нередко как непосредственно после соответствующего занятия, так и в качестве вопроса «с подвохом» на модулях и экзаменах.

Вот почему стоит рассмотреть типовые задачи и методы их решения.

Имеет ли смысл выражение:

Необходимо произвести все вычисление в скобках и привести выражение к виду:

Конечный результат содержит деление на ноль, следовательно, выражение не имеет смысла.

Какие выражения не имеют смысла?

Следует вычислить конечное значение для каждого из выражений.

Найти область допустимых значений для следующих выражений:

Область допустимых значений (ОДЗ) — это все те числа, при подставлении которых вместо переменных выражение будет иметь смысл.

То есть задание звучит как: найти значения, при которых не будет деления на ноль.

1) b є (-∞;-17) & (-17; + ∞), или b>-17 & b 25 & b 3 — x 2 y 3 + 13x — 38y)/(12x 2 — y).

Но на самом деле оно только выглядит страшным и громоздким, потому что на деле содержит в себе то, что уже давно известно: возведение чисел в квадрат и куб, некоторые арифметические действия, такие как деление, умножение, вычитание и сложения. Для удобства, между прочим, можно привести задачу к дробному виду.

Числитель у получившейся дроби не радует: (x 3 — x 2 y 3 + 13x — 38y). Это факт. Зато есть другой повод для счастья: его-то для решения задания трогать даже не понадобится! Согласно определению, рассмотренному ранее, делить нельзя на ноль, а что именно на него будет делиться, совершенно неважно. Потому оставляем это выражение в неизменном виде и подставляем пары чисел из данных вариантов в знаменатель. Уже третий пункт идеально вписывается, превращая небольшую скобочку в ноль. Но останавливаться на этом – плохая рекомендация, ведь подойти может еще что-нибудь. И вправду: пятый пункт тоже неплохо вписывается и подходит условию.

Записываем ответ: 3 и 5.

Видео:Задание №6 – Гдз по алгебре 8 класс (Мерзляк)Скачать

В заключение

Как видно, эта тема очень интересная и не особо сложная. Разобраться в ней не составит труда. Но все-таки отработать пару примеров никогда не помешает!

Видео:Выражение не имеет смысла. Алгебра 8 класс.Скачать

Область допустимых значений функции

О чем эта статья:

Видео:Когда алгебраическая дробь равна 0?Скачать

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Видео:При каких значениях переменной имеет смысл выражениеСкачать

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения 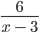— это числовое множество ( — ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:9кл. При каких значения переменной имеет смысл выражениеСкачать

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 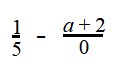— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки.

Например, если х > 6, но х

Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a — 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Видео:Допустимые значения переменной в рациональном выраженииСкачать

При каких значениях переменных не имеет смысла выражение: а) 5/2х- 4; б) 3/4y + 2; в) a/а — b; г) b/a + b?

Видео:При каких значениях x ... | ОГЭ 2017 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:249 Алгебра 8 класс, При каких значениях х имеет смысл выражениеСкачать

решение вопроса

Видео:Рациональные выражения. Алгебра, 8 классСкачать

Похожие вопросы

• Все категории
• экономические 43,415
• гуманитарные 33,633
• юридические 17,906
• школьный раздел 608,066
• разное 16,856

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🌟 Видео

Дробно-рациональные уравнения. 8 класс.Скачать

РАЦИОНАЛЬНЫЕ ДРОБИ . §1 алгебра 8 классСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

333 Алгебра 9 класс. Тема Решение Неравенств методом Интервалов примерыСкачать