При каких значениях переменной уравнение имеет смысла

теория по математике 📈 функции

Видео:8 класс. Алгебра. При каких значениях переменной имеет смысл выражениеСкачать

Определение понятия функции. Переменные.

Зависимость переменной у от переменной х, при которой любому значению переменной х соответствует единственное значение переменной у, называют функцией.

• х – это независимая переменная, ее называют аргумент.
• у – это зависимая переменная.

Ключевое слово, которое нужно запомнить в определении функции – это зависимость.

Например, человек идет на деловую встречу, но чувствует, что он опаздывает. Он ускоряет свой шаг, потому что от его скорости зависит время. Чем быстрее он двигается, тем меньше времени уйдет у него на дорогу. То есть время зависит от скорости.

Или, например, спортсмен метает ядро на дальнее расстояние. Чем сильнее будет бросок, тем дальше полетит ядро. Скорость полета зависит от силы толчка. Здесь опять прослеживается зависимость.

Например, функция задана формулой у = – 3х 2 – 7. Равносильная ей запись такая: f(x)= – 3х 2 – 7.

Видео:Вариант 36, № 3. Значение переменной, при котором выражение (дробь) не имеет смысла. Пример 1Скачать

Области определения и значения функции

Все возможные значения независимой переменной (х) называют областью определения функции.

Все значения, которые принимает зависимая переменная (у) называют областью значений функции.

Если какая-либо функция у=f(x) задана формулой, а при этом ее область определения не указана, то считается, что она состоит из любых значений переменной, при которых выражение имеет смысл.

Области определения и значений школьных функций

1. Для линейной функции областью определения будет являться любое число.

Если у такой функции k≠0, то областью ее значений также будет являться любое число.

При k=0 область значений этой функции состоит из единственного числа b.

Например, функция задана формулой у = 7. Тогда ее область значения — это число 7, а область определения – любое число.

2. Гипербола задается формулой вида y = k/x.

Область определения такой функции – любое число, кроме нуля.

Область значений такой функции – аналогичная.

3. Функция, заданная формулой y= |x|, имеет область определения – любое число.

4. У функций у = х 2 и у = х 3 область определения – любое число.

Для того чтобы понимать, как находится область определения функции и рассмотреть примеры заданий на нахождение области определения функции, вспомним правила, при которых существуют ограничения и выражение не имеет смысл: нельзя делить на нуль; нельзя извлекать квадратный корень из отрицательного числа.

Пример 3. Рассмотрим, как находится область определения функций, которые заданы следующими формулами:

• у = 5х + 2

Данное выражение будет иметь смысл при любом значении х, так как все действия здесь выполнимы. Например, подставив нуль, получим, что 5×0 + 2 = 2. Также при любых отрицательных или положительных значениях х выражение будет иметь смысл.

• у = – 8х 2 – 4

Данное выражение содержит степень. Все действия здесь так же выполнимы при любом значении х.

• у = 87/(х + 11)

В знаменателе этого выражения содержится переменная х, поэтому надо проверить, при каком значении он может быть равным нулю и исключить это значение из области определения, так как на знаменатель делят, а на нуль делить нельзя.

Итак, имеем знаменатель х + 11. Приравниваем его к нулю, получаем х + 11 = 0. Решаем простое уравнение на нахождение неизвестного слагаемого и получаем х= – 11. Это число исключаем из области определения функции.

• у = √х

Выражение содержит квадратный корень из переменной х. Знаем, что он может извлекаться только из положительного или равного нулю числа. Поэтому область определения будет х≥0.

Ответ: (1) и (2) – множество всех чисел; (3) – любое число, кроме (-11) или х ≠ – 11; (4) х ≥0.

Нахождение области определения функции

1. Если выражение целое и не содержит квадратного корня, то оно имеет смысл при любом значении независимой переменной. Следовательно, областью определения будет являться множество всех чисел.
2. Если выражение дробное, то необходимо исключить те значения, которые обращают знаменатель в нуль. Для этого знаменатель дроби приравнять к нулю и решить полученное уравнение. Областью определения будут являться все числа, кроме тех, которые получились при решении уравнения.

Видео:Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать

Уравнения с одной переменной

Уравнением с одной переменной — это равенство, содержащее только одну переменную. Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.

Содержание:

Определение уравнения. Корни уравнения

Равенство с переменной f(x) = g (х) называют уравнением с одной переменной х, если поставлена задача найти все те же значения х, при которых равенство с переменной обращается в верное числовое равенство. Всякое значение переменной, при котором выражения /(х) и g(x) принимают равные числовые значения, называют корнем уравнения.

Решить уравнение — это значит найти все его корни или доказать, что их нет.

Пример 1.

Уравнение 3 + х = 7 имеет единственный корень 4, так как при этом и только при этом значении переменной равенство 3 + х = 7 является верным.

Пример 2.

Уравнение (х — 1)(х — 2) = 0 имеет два корня: 1 и 2.

Пример 3.

Уравнение не имеет действительных корней.

Заметим, что можно говорить и о мнимых корнях уравнений. Так, уравнение имеет два мнимых корня: (см. п. 47). Всюду ниже речь идет только о действительных корнях уравнений.

Равносильность уравнений

Уравнения, имеющие одни и те же корни, называют равносильными. Равносильными считаются и уравнения, каждое из которых не имеет корней.

Например, уравнения х + 2 = 5 и х + 5 = 8 равносильны, так как каждое из них имеет единственный корень — число 3. Равносильны и уравнения — ни одно из них не имеет корней.

Уравнения неравносильны, так как первое имеет только один корень 6, тогда как второе имеет два корня: 6 и — 6.

В процессе решения уравнения его стараются заменить более простым, но равносильным данному. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.

Теорема 1.

Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.

Например, уравнение равносильно уравнению

Теорема 2.

Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Например, уравнение равносильно уравнению (обе части первого уравнения мы умножили на 3).

Линейные уравнения

Линейным уравнением с одной переменной х называют уравнение вида

где — действительные числа; называют коэффициентом при переменной, — свободным членом.

Для линейного уравнения могут представиться три случая:

1) ; в этом случае корень уравнения равен ;

2) ; в этом случае уравнение принимает вид , что верно при любом х, т. е. корнем уравнения служит любое действительное число;

3) ; в этом случае уравнение принимает вид , оно не имеет корней.

Многие уравнения в результате преобразований сводятся к линейным.

Пример 1.

Решить уравнение

Решение:

По теореме 1 (см. п. 135), данное уравнение равносильно уравнению . Если разделить обе части этого уравнения на коэффициент при х, то по теореме 2 получим равносильное данному уравнение . Итак, — корень уравнения.

Пример 2.

Решение:

Это уравнение сводится к линейному уравнению. Умножив обе части уравнения на 12 (наименьшее общее кратное знаменателей 3, 4, 6,12), получим

Квадратные уравнения

где — действительные числа, причем , называют квадратным уравнением. Если , то квадратное уравнение называют приведенным, если , то неприведенным. Коэффициенты имеют следующие названия: — первый коэффициент, — второй коэффициент, с — свободный член. Корни уравнения находят по формуле

Выражение называют дискриминантом квадратного уравнения (1). Если D О, то уравнение имеет два действительных корня.

В случае, когда D = О, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Используя обозначение , можно переписать формулу (2) в виде Если , то формулу (2) можно упростить:

Формула (3) особенно удобна, если — целое число, т. е. коэффициент — четное число.

Пример 1.

Решение:

Здесь . Имеем:

Так как , то уравнение имеет два корня, которые найдем по формуле (2):

Итак, — корни заданного уравнения.

Пример 2.

Решить уравнение

Решение:

Здесь По формуле (3) находим т. е. х = 3 — единственный корень уравнения.

Пример 3.

Решить уравнение

Решение:

Здесь Так как D 0, откуда х>3, и 5 — х > 0, откуда х 5, тогда как для уравнения (2) областью определения служит вся числовая прямая. Поэтому найденное значение х = 4, являющееся корнем уравнения (2), может оказаться посторонним корнем для уравнения (1). В данном случае именно это и происходит, поскольку х = 4 не принадлежит области определения уравнения (1) (не удовлетворяет неравенству х > 5). Итак, х = 4 — посторонний корень, т. е. заданное уравнение не имеет корней.

Рациональные уравнения

Уравнение f(x) = g(x) называют рациональным, если f(x) и g(x) — рациональные вьфажения. При этом если f(x) и g(x) — целые выражения, то уравнение называют целым; если же хотя бы одно из выражений f(х), g(x) является дробным, то рациональное уравнение f(x) = g(x) называют дробным.

Например, целыми являются линейные (см. п. 136), квадратные (см. п. 137) уравнения.

Чтобы решить рациональное уравнение, нужно:

1) найти общий знаменатель всех имеющихся дробей;

2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль общий знаменатель.

Пример:

Решение:

Общим знаменателем имеющихся дробей является 2х(2 — х). Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем:

Из уравнения находим (см. п. 137). Осталось проверить, обращают ли найденные корни выражение 2х(2 — х) в нуль, т. е. проверить выполнение условия Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит, х = 4 — единственный корень уравнения.

Решение уравнения р(х) = 0 методом разложения его левой части на множители

Суть этого метода состоит в следующем. Пусть нужно решить уравнение р(х) = 0, где р(х) — многочлен степени . Предположим, что удалось разложить многочлен на множители:, где — многочлены более низкой степени, чем . Тогда уравнение р(х) = 0 принимает вид . Если — корень уравнения а потому хотя бы одно из чисел равно нулю.

Значит, — корень хотя бы одного из уравнений

Верно и обратное: если — корень хотя бы одного из уравнений то — корень уравнения т. е. уравнения р (х) = 0.

Итак, если , где — многочлены, то вместо уравнения р(х) = 0 нужно решить совокупность уравнений Все найденные корни этих уравнений, и только они, будут корнями уравнения р(х) = 0.

Пример 1.

Решить уравнение

Решение:

Разложим на множители левую часть уравнения. Имеем откуда

Значит, либо х + 2 = 0, либо . Из первого уравнения находим х = — 2, второе уравнение не имеет корней. Итак, получили ответ: -2.

Метод разложения на множители применим к любым уравнениям вида р(х) = 0, где р(х) необязательно многочлен. Пусть но среди выражений есть выражения более сложного вида, чем многочлены (например, иррациональные, логарифмические и т. д.). Среди корней уравнений могут быть посторонние для уравнения р(х) = 0.

Пример 2.

Решить уравнение

Решение:

Имеем ; значит, либо , либо .Из уравнения находим х = 0, из уравнения находим .

Но х = -3 не удовлетворяет исходному уравнению, так как при этом значении не определено выражение . Это посторонний корень.

Итак, уравнение имеет два корня: 3; 0.

Решение уравнений методом введения новой переменной

Суть этого метода поясним на примерах.

Пример 1.

Решение:

Положив , получим уравнение

откуда находим . Теперь задача сводится к решению совокупности уравнений

Первое квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен.

Из второго квадратного уравнения находим . Это корни заданного уравнения.

Пример 2.

Решение:

Положим , тогда

и уравнение примет вид

Решив это уравнение (см. п. 145), получим

Но . Значит, нам остается решить совокупность уравнений

Из первого уравнения находим , ; из второго уравнения получаем Тем самым найдены четыре корня заданного уравнения.

Биквадратные уравнения

Биквадратным уравнением называют уравнение вида

Биквадратное уравнение решается методом введения новой переменной: положив , придем к квадратному уравнению

Пример:

Решить уравнение .

Решение:

Положив , получим квадратное уравнение , откуда находим . Теперь задача сводится к решению совокупности уравнений Первое уравнение не имеет действительных корней, из второго находим Это — корни заданного биквадратного уравнения.

Решение задач с помощью составления уравнений

С помощью уравнений решаются многочисленные задачи, к которым приводят самые разнообразные вопросы физики, механики, экономики и т. д. Прежде всего напомним общий порядок решения задач с помощью уравнений.

1) Вводят переменные, т. е. буквами х, у, z обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.

2) С помощью введенных переменных и данных в задаче чисел и их соотношений составляют систему уравнений (или одно уравнение).

3) Решают составленную систему уравнений (или уравнение) и из полученных решений отбирают те, которые подходят по смыслу задачи.

4) Если буквами х, у, z обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.

Задача 1.

Для перевозки 60 т груза из одного места в другое затребовали некоторое количество машин. Ввиду неисправности дороги на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, поэтому дополнительно потребовались 4 машины. Какое количество машин было затребовано первоначально?

Решение: Обозначим через х количество машин, затребованных первоначально. Тогда на самом деле было вызвано (х + 4) машин. Так как надо было перевезти 60 т груза, то предполагалось, что на одну машину будут грузить т груза, а на самом деле грузили т груза, что на 0,5 т меньше, чем предполагалось. В результате мы приходим к уравнению

Это уравнение имеет два корня: х = -24, х = 20. Ясно, что по смыслу задачи значение х = —24 не подходит. Таким образом, первоначально было затребовано 20 машин.

Задача 2.

Моторная лодка, движущаяся со скоростью 20 км/ч, прошла расстояние между двумя пунктами по реке туда и обратно без остановок за 6 ч 15 мин. Расстояние между пунктами равно 60 км. Найти скорость течения реки.

Решение:

Пусть х км/ч — скорость течения реки. Тогда лодка, собственная скорость которой 20 км/ч, идет по течению со скоростью (20 + х) км/ч, а против течения — со скоростью (20 — х) км/ч. Время, за которое лодка пройдет путь между пунктами по течению, составит ч, а время, за которое лодка пройдет обратный путь, составит ч. Так как путь туда и обратно лодка проходит за 6 ч 15 мин, т. е. ч, приходим к уравнению

решив которое, находим два корня: х = 4, х = -4. Ясно, что значение х = -4 не подходит по смыслу задачи. Итак, скорость течения реки равна 4 км/ч.

Задача 3.

Найти двузначное число, зная, что цифра его единиц на 2 больше цифры десятков и что произведение искомого числа на сумму его цифр равно 144.

Решение:

Напомним, что любое двузначное число может быть записано в виде 10х + у, где х — цифра десятков, а у — цифра единиц. Согласно условию, если х — цифра десятков, то цифра единиц равна х + 2 и мы получаем

Решив это уравнение, найдем

Второй корень не подходит по смыслу задачи.

Итак, цифра десятков равна 2, цифра единиц равна 4; значит, искомое число равно 24.

Задача 4.

Двое рабочих, работая вместе, выполнили некоторую работу за 6 ч. Первый из них, работая отдельно, может выполнить всю работу на 5 ч скорее, чем второй рабочий, если последний будет работать отдельно. За сколько часов каждый из них, работая отдельно, может выполнить всю работу?

Решение:

Производительность труда, т. е. часть работы, выполняемая в единицу времени (обозначим ее через А), и время, необходимое для выполнения всей работы (обозначим его через t), — взаимно обратные величины, т. е. At = 1. Поэтому если обозначить через х ч время, необходимое для выполнения всей работы первому рабочему, а через (х + 5) ч — второму, то часть работы, выполняемая первым рабочим за 1 ч, равна , а часть работы, выполняемая вторым рабочим за 1 ч, равна Согласно условию, они, работая вместе, выполнили всю работу за 6 ч. Доля работы, выполненная за 6 ч первым рабочим, есть , а доля работы, выполненная за 6 ч вторым рабочим, есть Так как вместе они выполнили всю работу, т. е. доля выполненной работы равна 1, получаем уравнение

решив которое, найдем х = 10.

Итак, первый рабочий может выполнить всю работу за 10 ч, а второй — за 15 ч.

Задача 5.

Из сосуда емкостью 54 л, наполненного кислотой, вылили несколько литров и долили сосуд водой, потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 л чистой кислоты. Сколько кислоты вылили в первый раз?

Решение:

Пусть в первый раз было вылито х л кислоты. Тогда в сосуде осталось (54 — х) л кислоты. Долив сосуд водой, получили 54 л смеси, в которой растворилось (54 — х) л кислоты. Значит, в 1 л смеси содержится л кислоты (концентрация раствора). Во второй раз из сосуда вылили х л смеси, в этом количестве смеси содержалось л кислоты. Таким образом, в первый раз было вылито х л кислоты, во второй л кислоты, а всего

за два раза вылито 54 — 24 = 30 л кислоты. В результате приходим к уравнению

Решив это уравнение, найдем два корня: и . Ясно, что значение 90 не удовлетворяет условию задачи.

Итак, в первый раз было вылито 18 л кислоты.

Задача 6.

Имеется кусок сплава меди с оловом массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 40% меди?

Решение:

Пусть масса добавленного олова составляет х кг. Тогда получится сплав массой (12 + х) кг, содержащий 40% меди. Значит, в новом сплаве имеется 0,4(12 + х) кг меди. Исходный сплав массой 12 кг содержал 45% меди, т. е. меди в нем было . Так как масса меди и в имевшемся, и в новом сплаве одна и та же, приходим к уравнению

Решив это уравнение, получим х = 1,5. Таким образом, к исходному сплаву надо добавить 1,5 кг олова.

Задача 7.

Имеется сталь двух сортов с содержанием никеля 5% и 40%. Сколько стали того и другого сорта надо взять, чтобы после переплавки получить 140 т стали с содержанием никеля 30% ?

Решение:

Пусть масса стали первого сорта равна х т, тогда стали второго сорта надо взять (140 — х) т. Содержание никеля в стали первого сорта составляет 5%; значит, в х т стали первого сорта содержится 0,05л; т никеля. Содержание никеля в стали второго сорта составляет 40%; значит, в (140 — х) т стеши второго сорта содержится 0,4 (140 — х) т никеля. По условию после соединения взятых двух сортов должно получиться 140 т стали с 30% -ным содержанием никеля, т. е. после переплавки в полученной стали должно быть 0,3 * 140 т никеля. Но это количество никеля складывается из 0,05л; т, содержащихся в стали первого сорта, и из 0,4 (140 — х) т, содержащихся в стали второго сорта. Таким образом, приходим к уравнению

0,05х + 0,4 (140 — х) = 0,3 * 140,

из которого находим х = 40. Следовательно, надо взять 40 т стали с 5% -ным и 100 т стали с 40% -ным содержанием никеля.

Иррациональные уравнения

Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень. Например, иррациональными являются уравнения

Используются два основных метода решения иррациональных уравнений:

1) метод возведения обеих частей уравнения в одну и ту же степень;

2) метод введения новых переменных (см. п. 147).

Метод возведения обеих частей уравнения в одну

и ту же степень состоит в следующем:

а) преобразуют заданное иррациональное уравнение к виду

б) возводят обе части полученного уравнения в п-ю степень:

в) учитывая, что , получают уравнение

г) решают уравнение и, в случае четного п, делают проверку, так как возведение обеих частей уравнения в одну и ту же четную степень может привести к появлению посторонних корней (см. п. 142). Эта проверка чаще всего осуществляется с помощью подстановки найденных значений переменной в исходное уравнение.

Пример 1.

Решить уравнение

Решение:

Возведем обе части уравнения в шестую степень; получим х — 3 = 64, откуда х = 67.

Проверка:

Подставив 67 вместо х в данное уравнение, получим , т. е. 2 = 2 — верное равенство.

Ответ: 67.

Пример 2.

Решение:

Преобразуем уравнение к виду

и возведем обе части его в квадрат. Получим

Еще раз возведем обе части уравнения в квадрат:

откуда

Проверка:

1) При х = 5 имеем

— верное равенство.

Таким образом, х = 5 является корнем заданного уравнения.

2) При х = 197 имеем Таким образом, х = 197 — посторонний корень.

Ответ: 5.

Пример 3.

Решение:

Применим метод введения новой переменной.

Положим и мы получаем уравнение , откуда находим

Теперь задача свелась к решению совокупности уравнений

Возведя обе части уравнения в пятую степень, получим х — 2 = 32, откуда х = 34.

Уравнение не имеет корней, поскольку под знаком возведения в дробную степень может содержаться только неотрицательное число, а любая степень неотрицательного числа неотрицательна.

Ответ: 34.

Показательные уравнения

Показательное уравнение вида

где равносильно уравнению f(х) = g(x).

Имеются два основных метода решения показательных уравнений:

1) метод уравнивания показателей, т. е. преобразование заданного уравнения к виду а затем к виду f(х) = g(x);

2) метод введения новой переменной.

Пример 1.

Решить уравнение

Решение:

Данное уравнение равносильно уравнению откуда находим Решив это квадратное уравнение, получим

Пример 2.

Решение:

Приведем все степени к одному основанию . Получим уравнение которое преобразуем к виду Уравнение равносильно уравнению х = 2х — 3, откуда находим х = 3.

Пример 3.

Решить уравнение

Решение:

Применим метод введения новой переменной. Так как ,то данное уравнение можно переписать в виде

Введем новую переменную, положив Получим квадратное уравнение с корнями Теперь задача сводится к решению совокупности уравнений

Из первого уравнения находим х = 2. Второе уравнение не имеет корней, так как при любых значениях х.

Ответ: 2.

Логарифмические уравнения

Чтобы решить логарифмическое уравнение вида

где нужно:

1) решить уравнение f(x) = g(x);

2) из найденных корней отобрать те, которые удовлетворяют неравенствам f(x) > 0 и g(x) > 0; остальные корни уравнения f(x) = g(x) являются посторонними для уравнения (1).

Имеются два основных метода решения логарифмических уравнений:

1) метод, заключающийся в преобразовании уравнения к виду затем к виду f(x) = g(x);

2) метод введения новой переменной.

Пример 1.

Решение:

Перейдем от заданного уравнения к уравнению и решим его. Имеем Проверку найденных значений х выполним с помощью неравенств Число -3 этим неравенствам удовлетворяет, а число 4 — нет. Значит, 4 — посторонний корень.

Ответ: -3.

Пример 2.

Решение:

Воспользовавшись тем, что сумма логарифмов равна логарифму произведения (см. п. 120), преобразуем уравнение к виду

Из последнего уравнения находим

Осталось сделать проверку. Ее можно выполнить с помощью системы неравенств

Подставив поочередно найденные значения -1 и -5,5 в эти неравенства, убеждаемся, что -1 удовлетворяет всем неравенствам, а -5,5 — нет, например при этом значении не выполняется первое неравенство. Значит, -5,5 — посторонний корень.

Ответ: -1.

Пример 3.

Решение:

Так как заданное уравнение можно переписать следующим образом:

Введем новую переменную, положив Получим

Но ; из уравнения находим х = 4.

Ответ: 4.

Примеры решения показательно-логарифмических уравнений

Пример 1.

Решение:

Область определения уравнения: х > 0. При этом условии выражения, входящие в обе части уравнения (1), принимают только положительные значения. Прологарифмировав обе части уравнения (1) по основанию 10, получим уравнение

равносильное уравнению (1). Далее имеем

Полагая получим уравнение , откуда Остается решить совокупность уравнений Из этой совокупности получим — корни уравнения (1).

Здесь применен метод логарифмирования, заключающийся в переходе от уравнения f(x) = g(x) к уравнению

Пример 2.

(2)

Решение:

Воспользовавшись определением логарифма, преобразуем уравнение (2) к виду

Полагая , получим уравнение корнями которого являются

Теперь задача сводится к решению совокупности уравнений

Так как , а -1 0 и мы получаем

если , то D = 0 и мы получаем , т. е. (поскольку ) .

Итак, если то действительных корней нет; если = 1, то ; если ,то ; если и , то

Пример 3.

При каких значениях параметра уравнение

имеет два различных отрицательных корня?

Решение:

Так как уравнение должно иметь два различных действительных корня его дискриминант должен быть положительным. Имеем

Значит, должно выполняться неравенство

По теореме Виета для заданного уравнения имеем

Так как, по условию, , то и

В итоге мы приходим к системе неравенств (см. п. 177):

Из первого неравенства системы находим (см. п. 180, 183) ; из второго ; из третьего . С помощью координатной прямой (рис. 1.107) находим, что либо , либо

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:При каких значениях переменной имеет смысл выражениеСкачать

Выражение, не имеющее смысла: примеры

Выражение – это самый широкий математический термин. По существу, в этой науке из них состоит все, и все операции проводятся тоже над ними. Другой вопрос, что в зависимости от конкретного вида применяются совершенно разнообразные методы и приемы. Так, работа с тригонометрией, дробями или логарифмами – это три различных действия. Выражение, не имеющее смысла, может относится к одному из двух видов: числовому или алгебраическому. А вот что означает это понятие, как выглядит его пример и прочие моменты будут рассмотрены далее.

Видео:Установите при каких значениях переменной не имеет смысла алгебраическая дробьСкачать

Числовые выражения

Если выражение состоит из чисел, скобок, плюсов-минусов и остальных знаков арифметических действий, его смело можно называть числовым. Что довольно логично: стоит только еще разок взглянуть на первый названный его компонент.

Числовым выражением может быть что угодно: главное, чтобы в нем не было букв. А под «чем угодно» в данном случае понимается все: от простой, стоящей одиноко, самой по себе, цифры, до огромного их перечня и знаков арифметических действий, требующих последующего вычисления конечного результата. Дробь – это тоже числовое выражение, если в ней нет всяких a, b, c, d и т.д., ведь тогда это совершенно другой вид, о котором будет рассказано чуть позже.

Видео:Задача №39. Алгебра 7 класс Макарычев.Скачать

Условия для выражения, которое не имеет смысла

Когда задание начинается со слова «вычислить», можно говорить о преобразовании. Штука в том, что это действие не всегда целесообразно: в нем не то чтобы сильно нуждаются, если на передний план выходит выражение, не имеющее смысла. Примеры бесконечно удивительны: иногда, чтобы понять, что оно-то нас и настигло, приходится долго и нудно раскрывать скобки и считать-считать-считать.

Главное, что нужно запомнить: не имеет смысла то выражения, чей конечный результат сводится к запретному в математике действию. Если уж совсем по-честному, то тогда бессмысленным становится само преобразование, но для того, чтобы это выяснить, приходится его для начала выполнить. Такой вот парадокс!

Самое знаменитое, но от того не менее важное запретное математическое действие – это деление на ноль.

Потому вот, например, выражение, не имеющее смысла:

Если при помощи нехитрых вычислений свести вторую скобку к одной цифре, то она и будет нулем.

По такому же принципу «почетное звание» дается и этому выражению:

Видео:Как найти значения переменной, при которых алгебраическая дробь не имеет смысла?Скачать

Алгебраические выражения

Это то же самое числовое выражение, если в него добавить запретные буквы. Тогда оно и становится полноценным алгебраическим. Оно также может быть всех размеров и форм. Алгебраическое выражение – понятие более широкое, включающее в себя предыдущее. Но был смысл начинать разговор не с него, а с числового, чтобы было понятнее и разобраться было легче. Ведь имеет ли смысл выражение алгебраическое – вопрос не то чтобы очень сложный, но имеющий больше уточнений.

Видео:9кл. При каких значения переменной имеет смысл выражениеСкачать

Почему так?

Буквенное выражение, или выражение с переменными – это синонимы. Первый термин объяснить просто: ведь оно, в конце концов, содержит в себе буквы! Второй тоже не загадка века: вместо букв можно подставлять разные числа, вследствие чего значение выражения будет меняться. Нетрудно догадаться, что буквы в данном случае и есть переменные. По аналогии, числа – это постоянные.

И тут мы возвращаемся к основной тематике: что такое выражение, не имеющее смысла?

Видео:Задание №6 – Гдз по алгебре 8 класс (Мерзляк)Скачать

Примеры алгебраических выражений, не имеющих смысла

Условие для бессмысленности алгебраического выражения — аналогичное, как и для числового, с одним лишь только исключением, а если быть точнее, дополнением. При преобразовании и вычислении конечного результата приходится учитывать переменные, поэтому вопрос ставится не как «какое выражение не имеет смысла?», а «при каком значении переменной это выражение не будет иметь смысла?» и «есть ли такое значение переменной, при котором выражение потеряет смысл?»

Вышеприведенное выражение не имеет смысла при a равном -2.

А вот насчет (a+3):(12-4-8) можно смело сказать, что это выражение, не имеющее смысла при любых a.

Точно так же, какое b ни подставишь в выражение (b — 11):(12+1), оно по-прежнему будет иметь смысл.

Видео:Выражение не имеет смысла. Алгебра 8 класс.Скачать

Типовые задачи по теме «Выражение, не имеющее смысла»

7 класс изучает эту тему по математике в числе прочих, и задания по ней встречаются нередко как непосредственно после соответствующего занятия, так и в качестве вопроса «с подвохом» на модулях и экзаменах.

Вот почему стоит рассмотреть типовые задачи и методы их решения.

Имеет ли смысл выражение:

Необходимо произвести все вычисление в скобках и привести выражение к виду:

Конечный результат содержит деление на ноль, следовательно, выражение не имеет смысла.

Какие выражения не имеют смысла?

Следует вычислить конечное значение для каждого из выражений.

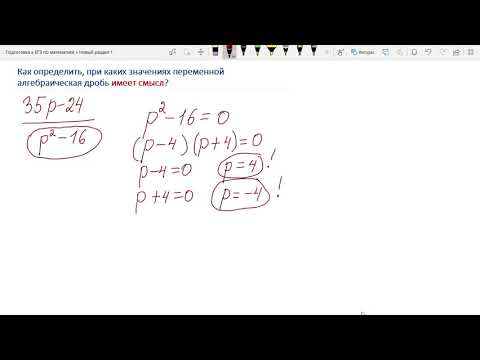
Найти область допустимых значений для следующих выражений:

Область допустимых значений (ОДЗ) — это все те числа, при подставлении которых вместо переменных выражение будет иметь смысл.

То есть задание звучит как: найти значения, при которых не будет деления на ноль.

1) b є (-∞;-17) & (-17; + ∞), или b>-17 & b 25 & b 3 — x 2 y 3 + 13x — 38y)/(12x 2 — y).

Но на самом деле оно только выглядит страшным и громоздким, потому что на деле содержит в себе то, что уже давно известно: возведение чисел в квадрат и куб, некоторые арифметические действия, такие как деление, умножение, вычитание и сложения. Для удобства, между прочим, можно привести задачу к дробному виду.

Числитель у получившейся дроби не радует: (x 3 — x 2 y 3 + 13x — 38y). Это факт. Зато есть другой повод для счастья: его-то для решения задания трогать даже не понадобится! Согласно определению, рассмотренному ранее, делить нельзя на ноль, а что именно на него будет делиться, совершенно неважно. Потому оставляем это выражение в неизменном виде и подставляем пары чисел из данных вариантов в знаменатель. Уже третий пункт идеально вписывается, превращая небольшую скобочку в ноль. Но останавливаться на этом – плохая рекомендация, ведь подойти может еще что-нибудь. И вправду: пятый пункт тоже неплохо вписывается и подходит условию.

Записываем ответ: 3 и 5.

Видео:Допустимые значения переменной в рациональном выраженииСкачать

В заключение

Как видно, эта тема очень интересная и не особо сложная. Разобраться в ней не составит труда. Но все-таки отработать пару примеров никогда не помешает!

🔍 Видео

249 Алгебра 8 класс, При каких значениях х имеет смысл выражениеСкачать

Когда алгебраическая дробь равна 0?Скачать

Алгебраические выражения. Практическая часть. 6 класс.Скачать

РАЦИОНАЛЬНЫЕ ДРОБИ . §1 алгебра 8 классСкачать

АЛГЕБРА 7 класс : Выражения с переменнымиСкачать

Рациональные выражения. Алгебра, 8 классСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

333 Алгебра 9 класс. Тема Решение Неравенств методом Интервалов примерыСкачать

Урок 2 ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ 7 КЛАСССкачать