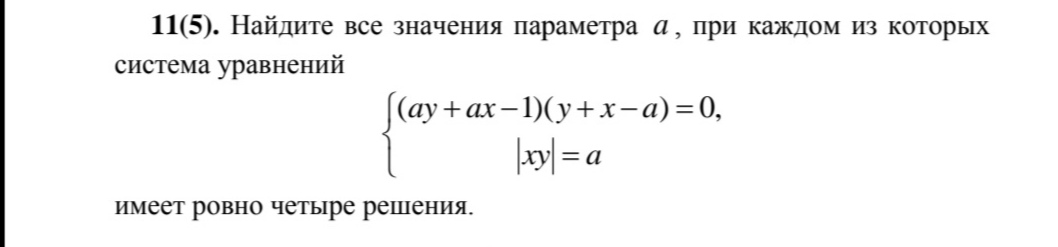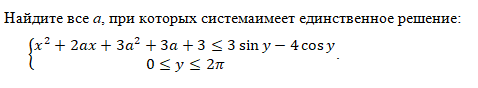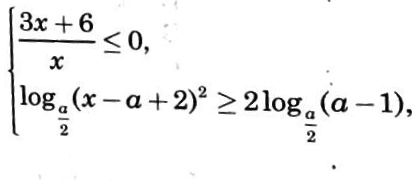При каких значениях параметра а система уравнений имеет только одно решение

Видео:#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать

Урок по теме «Решение систем линейных уравнений, содержащих параметры»

Разделы: Математика

Если в задаче меньше трех переменных, это не задача; если больше восьми – она неразрешима. Энон.

Задачи с параметрами встречаются во всех вариантах ЕГЭ, поскольку при их решении наиболее ярко выявляется, насколько глубоки и неформальны знания выпускника. Трудности, возникающие у учащихся при выполнении подобных заданий, вызваны не только относительной их сложностью, но и тем, что в учебных пособиях им уделяется недостаточно внимания. В вариантах КИМов по математике встречается два типа заданий с параметрами. Первый: «для каждого значения параметра решить уравнение, неравенство или систему». Второй: «найти все значения параметра, при каждом из которых решения неравенства, уравнения или системы удовлетворяют заданным условиям». Соответственно и ответы в задачах этих двух типов различаются по существу. В первом случае в ответе перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. Во втором – перечисляются все значения параметра, при которых выполнены условия задачи. Запись ответа является существенным этапом решения, очень важно не забыть отразить все этапы решения в ответе. На это необходимо обращать внимание учащихся.
В приложении к уроку приведен дополнительный материал по теме «Решение систем линейных уравнений с параметрами», который поможет при подготовке учащихся к итоговой аттестации.

• систематизация знаний учащихся;
• выработка умений применять графические представления при решении систем уравнений;
• формирование умения решать системы линейных уравнений, содержащих параметры;
• осуществление оперативного контроля и самоконтроля учащихся;
• развитие исследовательской и познавательной деятельности школьников, умения оценивать полученные результаты.

Урок рассчитан на два учебных часа.

Ход урока

1. Организационный момент

Сообщение темы, целей и задач урока.

1. Актуализация опорных знаний учащихся

Проверка домашней работы. В качестве домашнего задания учащимся было предложено решить каждую из трех систем линейных уравнений

а) б) в)

графически и аналитически; сделать вывод о количестве полученных решений для каждого случая

Ответы:

Заслушиваются и анализируются выводы, сделанные учащимися. Результаты работы под руководством учителя в краткой форме оформляются в тетрадях.

В общем виде систему двух линейных уравнений с двумя неизвестными можно представить в виде: .

Решить данную систему уравнений графически – значит найти координаты точек пересечения графиков данных уравнений или доказать, что таковых нет. Графиком каждого уравнения этой системы на плоскости является некоторая прямая.

Возможны три случая взаимного расположения двух прямых на плоскости:

1. если (если хотя бы один из знаменателей равен нулю, последнее неравенство надо понимать как ), то прямые пересекаются в одной точке; в этом случае система имеет единственное решение

1. если то прямые не имеют общих точек, т.е. не пересекаются; а значит, система решений не имеет

1. если то прямые совпадают. В этом случае система имеет бесконечно много решений

К каждому случаю полезно выполнить рисунок.

Сегодня на уроке мы научимся решать системы линейных уравнений, содержащие параметры. Параметром будем называть независимую переменную, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству. Решить систему уравнений с параметром – значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество решений системы.

Решение задачи с параметром зависит от вопроса, поставленного в ней. Если нужно просто решить систему уравнений при различных значениях параметра или исследовать ее, то необходимо дать обоснованный ответ для любого значения параметра или для значения параметра, принадлежащего заранее оговоренному в задаче множеству. Если же необходимо найти значения параметра, удовлетворяющие определенным условиям, то полного исследования не требуется, и решение системы ограничивается нахождением именно этих конкретных значений параметра.

Пример 1. Для каждого значения параметра решим систему уравнений

1. Система имеет единственное решение, если

В этом случае имеем

1. Если а = 0, то система принимает вид

Система несовместна, т.е. решений не имеет.

1. Если то система запишется в виде

Очевидно, что в этом случае система имеет бесконечно много решений вида x = t; где t-любое действительное число.

• при система имеет единственное решение
• при а = 0 — нет решений;
• при а = 3 — бесконечно много решений вида где t R

Пример 2. При каких значениях параметра a система уравнений

• имеет единственное решение;
• имеет множество решений;
• не имеет решений?

• система имеет единственное решение, если
• подставим в пропорцию значение а = 1, получим , т.е. система имеет бесконечно много решений;
• при а = -1 пропорция примет вид: . В этом случае система не имеет решений.

• при система имеет единственное решение;
• при система имеет бесконечно много решений;
• при система не имеет решений.

Пример 3. Найдем сумму параметров a и b, при которых система

имеет бесчисленное множество решений.

Решение. Система имеет бесчисленное множество решений, если

То есть если a = 12, b = 36; a + b = 12 + 36 =48.

1. Закрепление изученного в ходе решения задач

1. № 15.24(а) [1]. Для каждого значения параметра решите систему уравнений

1. № 15.25(а) Для каждого значения параметра решите систему уравнений

1. При каких значениях параметра a система уравнений

а) не имеет решений; б) имеет бесконечно много решений.

Ответ: при а = 2 решений нет, при а = -2 бесконечное множество решений

1. Практическая работа в группах

Класс разбивается на группы по 4-5 человек. В каждую группу входят учащиеся с разным уровнем математической подготовки. Каждая группа получает карточку с заданием. Можно предложить всем группам решить одну систему уравнений, а решение оформить. Группа, первой верно выполнившая задание, представляет свое решение; остальные сдают решение учителю.

Карточка. Решите систему линейных уравнений

при всех значениях параметра а.

Ответ: при система имеет единственное решение ; при нет решений; при а = -1бесконечно много решений вида , (t; 1- t) где t R

Если класс сильный, группам могут быть предложены разные системы уравнений, перечень которых находится в Приложении1. Тогда каждая группа представляет классу свое решение.

Отчет группы, первой верно выполнившей задание

Участники озвучивают и поясняют свой вариант решения и отвечают на вопросы, возникшие у представителей остальных групп.

1. При каком значении k система имеет бесконечно много решений?
2. При каком значении p система не имеет решений?

1. При каком значении k система имеет бесконечно много решений?
2. При каком значении p система не имеет решений?

1. Итоги урока

Решение систем линейных уравнений с параметрами можно сравнить с исследованием, которое включает в себя три основных условия. Учитель предлагает учащимся их сформулировать.

При решении следует помнить:

1. для того, чтобы система имела единственное решение, нужно, чтобы прямые, отвечающие уравнению системы, пересекались, т.е. необходимо выполнение условия;
2. чтобы не имела решений, нужно, чтобы прямые были параллельны, т.е. выполнялось условие,
3. и, наконец, чтобы система имела бесконечно много решений, прямые должны совпадать, т.е. выполнялось условие.

Учитель оценивает работу на уроке класса в целом и выставляет отметки за урок отдельным учащимся. После проверки самостоятельной работы оценку за урок получит каждый ученик.

При каких значениях параметра b система уравнений

• имеет бесконечно много решений;
• не имеет решений?

Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.

• Найдите b и k,
• найдите координаты точки пересечения этих графиков.

Решите систему уравнений при всех значениях m и n.

Решите систему линейных уравнений при всех значениях параметра а (любую на выбор).

1. Алгебра и начала математического анализа: учеб. для 11 кл. общеобразоват. учреждений : базовый и профил. уровни / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин – М. : Просвещение, 2008.
2. Математика : 9 класс : Подготовка к государственной итоговой аттестации / М. Н. Корчагина, В. В. Корчагин – М. : Эксмо, 2008.
3. Готовимся в вуз. Математика. Часть 2. Учебное пособие для подготовки к ЕГЭ, участию в централизованном тестировании и сдаче вступительных испытаний в КубГТУ / Кубан. гос. технол. ун-т; Ин-т совр. технол. и экон.; Сост.: С. Н. Горшкова, Л. М. Данович, Н.А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар, 2006.
4. Сборник задач по математике для подготовительных курсов ТУСУР: Учебное пособие / З. М. Гольдштейн, Г. А. Корниевская, Г. А. Коротченко, С.Н. Кудинова. – Томск: Томск. Гос. ун-т систем управления и радиоэлектроники, 1998.
5. Математика: интенсивный курс подготовки к экзамену/ О. Ю. Черкасов, А.Г.Якушев. – М.: Рольф, Айрис-пресс, 1998.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Вторая часть.

В первой части мы рассматривали системы линейных алгебраических уравнений (СЛАУ), все коэффициенты которых были известны. В этой же части разберём СЛАУ, среди коэффициентов которых есть некий параметр. Для исследования СЛАУ на совместность станем использовать теорему Кронекера-Капелли. В процессе решения примеров на данной странице будем применять метод Гаусса или же метод Крамера. Сформулируем теорему и следствие из неё ещё раз:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.

Следствие из теоремы Кронекера-Капелли

Параметр $n$, использованный выше, равен количеству переменных рассматриваемой СЛАУ.

Исследовать СЛАУ $ left <begin& kx_1+2x_2+x_3=8;\ & -x_1+x_2+2x_3=7;\ & x_2+kx_3=5.endright.$ на совместность и найти решение системы в зависимости от значений параметра $k$.

Чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $widetilde$. Сделать это можно несколькими путями. Стоит учесть, что в данном примере нам требуется не только исследовать систему на совместность, но и указать её решения. Мне кажется наиболее удобным в таких задачах применять метод Гаусса, однако это вовсе не является обязательным. Для разнообразия данный пример решим методом Гаусса, а следующий – методом Крамера. Итак, запишем и начнём преобразовывать расширенную матрицу системы. При записи расширенной матрицы системы поменяем местами первую и вторую строки. Это нужно для того, чтобы первым элементом первой строки стало число -1.

$$ left(begin -1 & 1 &2 &7 \ k & 2 & 1 & 8\ 0 & 1 & k & 5 end right) begin phantom \ r_2+kcdot\ phantomendrightarrow left(begin -1 & 1 &2 &7 \ 0 & 2+k & 1+2k & 8+7k\ 0 & 1 & k & 5 end right)rightarrowleft|begin&text\&textendright|rightarrow \ rightarrow left(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 2+k & 1+2k & 8+7k end right) begin phantom\phantom\r_3-(2+k)cdotend rightarrow left(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2 end right) $$

Мы привели расширенную матрицу системы к ступенчатому виду. Напомню, что до черты расположена преобразованная матрица матрица системы: $left(begin-1 & 1 &2\0 & 1 & k\ 0 & 0 & 1-k^2end right)$.

Каким бы ни было значение параметра $k$, полученная нами после преобразований матрица будет содержать не менее двух ненулевых строк (первая и вторая строки точно останутся ненулевыми). Вопрос о количестве решений зависит лишь от третьей строки.

В следствии из теоремы Кронекера-Капелли указаны три случая, и в данном примере легко рассмотреть каждый из них. Начнём с варианта $rang Aneqrangwidetilde$, при котором система не имеет решений, т.е. несовместна.

Видео:№16 Задачи с параметром. ЕГЭ. Задание 18. При каких значениях параметра А система уравнений...Скачать

$rang Aneqrangwidetilde$

Ранги будут не равны друг другу лишь в одном случае: когда $1-k^2=0$, при этом $2k-2neq$. В этом случае преобразованная матрица системы будет содержать две ненулевых строки (т.е. $rang A=2$), а преобразованная расширенная матрица системы будет содержать три ненулевых строки (т.е. $rang widetilde=3$). Иными словами, нам требуется решить систему уравнений:

Из первого уравнения имеем: $k=1$ или $k=-1$, однако $kneq$, поэтому остаётся лишь один случай: $k=-1$. Следовательно, при $k=-1$ система не имеет решений.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

$rang A=rangwidetilde<3$

Рассмотрим второй пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой, но меньше, чем количество переменных (т.е. меньше 3). Это возможно лишь в том случае, если последняя строка преобразованной расширенной матрицы системы полностью станет нулевой, т.е.

Из данной системы имеем: $k=1$. Именно при $k=1$ третья строка преобразованной расширенной матрицы системы станет нулевой, поэтому $rang=rangwidetilde=2$. При этом, повторюсь, у нас всего три переменных, т.е. имеем случай $rang A=rangwidetilde=2<3$.

Система имеет бесконечное количество решений. Найдём эти решения. Подставим $k=1$ в преобразованную матрицу и продолжим операции метода Гаусса. Третью строку (она станет нулевой) просто вычеркнем:

$$ left(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2 end right)rightarrow|k=1|rightarrow left(begin -1 & 1 &2 &7 \0 & 1 & 1 & 5 end right) rightarrowleft|begin&text\&textendright|rightarrow \ rightarrowleft(begin-1 & 1 &-2 &7\0 & 1 & -1 & 5endright) begin r_1-r_2\phantomend rightarrowleft(begin-1 & 0 &-1 &2\0 & 1 & -1 & 5endright) begin -1cdot\phantomend rightarrowleft(begin1 & 0 &1 &-2\0 & 1 & -1 & 5endright) $$

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

$rang A=rangwidetilde=3$

Рассмотрим третий пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой и равны количеству переменных. Это возможно лишь в том случае, если $1-k^2neq$, т.е. $kneq$ и $kneq$. Продолжаем решение методом Гаусса:

$$ left(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2 endright)rightarrow left(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & (1-k)(1+k) & -2(1-k) endright) begin phantom\phantom\r_3:((1-k)(1+k))end rightarrow\ rightarrowleft(begin -1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1 & -2/(1+k) endright) begin r_1-2r_3\r_2-kcdot\phantomend rightarrow left(begin -1 & 1 &0 &(7k+11)/(k+1) \0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k) endright) begin r_1-r_2\phantom\phantomendrightarrow\ rightarrow left(begin -1 & 0 &0 &6/(k+1)\0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k) endright) begin -1cdot\phantom\phantomendrightarrow left(begin 1 & 0 &0 &-6/(k+1)\0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k) endright) $$

Исследовать СЛАУ $left <begin& 2kx_1+x_2+x_3=0;\ & x_1-x_2+kx_3=1;\ & (k-6)x_1+2x_2-4x_3=-3.endright.$ на совместность и найти решение системы при тех значениях параметра, при которых она совместна.

Вновь, как и в предыдущем примере, для того, чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $widetilde$. Чтобы исследовать систему на совместность и указать количество решений применим метод Крамера. Можно было бы решить и методом Гаусса, однако в предыдущем примере мы его уже использовали, поэтому для разнообразия решим задачу с помощью метода Крамера. Начнём с вычисления определителя матрицы системы. Этот определитель мы получим с помощью готовой формулы.

Значения переменных $x_1$, $x_2$, $x_3$ будут такими:

Нам остаётся исследовать совместность системы при условии $Delta=0$. Это равенство возможно при $k=0$ или $k=1$.

Видео:При каких положительных значениях параметра а система уравнений имеет единственное решениеСкачать

Случай $k=0$

Нам остаётся рассмотреть последний случай: $k=1$.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Случай $k=1$

Для наглядности я запишу здесь матрицу системы $A$ и расширенную матрицу системы $widetilde$, подставив $k=1$:

Если $k=1$, то $Delta=0$. Это значит, что $rang≤2$. Рассмотрим миноры второго порядка матрицы $A$. Например, возьмём минор, образованный на пересечении строк №1, №2 и столбцов №1, №2: $M=left|begin2 & 1\ 1 & -1endright|=-3$. Так как $Mneq$, то ранг матрицы $A$ равен 2.

Задача решена, осталось лишь записать ответ.

Разберём ещё один пример, в котором рассмотрим СЛАУ с четырьмя уравнениями.

Исследовать СЛАУ $ left <begin& kx_1+x_2+x_3+x_4=1;\ & x_1+kx_2+x_3+x_4=1;\ & x_1+x_2+kx_3+x_4=1;\ & x_1+x_2+x_3+kx_4=1.endright.$ на совместность и найти решение системы в зависимости от значений параметра $k$.

Применим метод Гаусса. При записи расширенной матрицы системы поместим первую строку вниз, на место четвёртой строки. А дальше начнём стандартные операции метода Гаусса.

$$ left(begin 1 & k &1 &1&1 \ 1 & 1 &k &1&1 \ 1 & 1 &1 &k&1 \ k & 1 &1 &1&1 end right) begin phantom\r_2-r_1\r_3-r_1\r_4-kcdotendrightarrow left(begin 1 & k &1 &1&1\ 0 & 1-k &k-1 &0&0\ 0 & 1-k &0&k-1&0\ 0 & 1-k^2 &1-k &1-k&1-kend right) $$

Здесь можно было бы остановиться и рассмотреть случаи $k=1$ и $kneq$ отдельно. Цель таких действий: разделить вторую, третью и четвёртую строки на $k-1$ при условии $k-1neq$. Однако пока что полученная нами матрица содержит не столь уж громоздкие элементы, поэтому сейчас отвлекаться на частности я не вижу смысла. Продолжим преобразования в общем виде:

$$ left(begin 1 & k &1 &1&1\ 0 & 1-k &k-1 &0&0\ 0 & 1-k &0&k-1&0\ 0 & 1-k^2 &1-k &1-k&1-kend right) begin phantom\phantom\r_3-r_2\r_4-(k+1)r_2endrightarrow \ rightarrow left(begin 1 & k &1 &1&1\ 0 & 1-k &k-1 &0&0\ 0 & 0 &1-k&k-1&0\ 0 & 0 &(1-k)(k+2) &1-k&1-kend right) begin phantom\phantom\phantom\r_4-(k+2)r_3endrightarrow \ rightarrow left(begin 1 & k &1 &1&1\ 0 & 1-k &k-1 &0&0\ 0 & 0 &1-k&k-1&0\ 0 & 0 &0&(1-k)(k+3)&1-kend right) $$

Мы привели расширенную матрицу системы к ступенчатому виду. До черты расположена преобразованная матрица системы. Ранги матриц $A$ и $widetilde$ зависят от значения параметра $k$. Рассмотрим три случая: $k=1$, $k=-3$ и случай $kneq$, $kneq$.

Видео:Математика | Параметр. Система уравнений с параметромСкачать

Случай $k=-3$

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Случай $k=1$

Если $k=1$, то преобразованная матрица станет такой: $left(begin 1 & 1 &1 &1&1\ 0 & 0 &0 &0&0\ 0 & 0 &0&0&0\ 0 & 0 &0&0&0endright)$. Ранги матрицы системы и расширенной матрицы системы равны между собой (и равны 1), но меньше, чем количество переменных, т.е. $rang=rang=1<4$. Вывод: система является неопределённой. Общее решение системы непосредственно получим из первой строки записанной матрицы:

$$x_1+x_2+x_3+x_4=1; Rightarrow ; x_1=-x_2-x_3-x_4+1.$$

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Случай $kneq$ и $neq$

Продолжим решение методом Гаусса. Так как $kneq$ и $neq$, то $(1-k)(k+3)neq$. Следовательно, мы можем разделить вторую и третью строки на $1-k$, четвёртую строку – на выражение $(1-k)(k+3)$. С полученной после этого матрицей продолжим операции обратного хода метода Гаусса:

$$ left(begin 1 & k &1 &1&1\ 0 & 1 &-1 &0&0\ 0 & 0 &1&-1&0\ 0 & 0 &0&1&fracend right) begin r_1-r_4\phantom\phantom\r_3+r_4endrightarrow left(begin 1 & k &1 &0&frac\ 0 & 1 &-1 &0&0\ 0 & 0 &1&0&frac\ 0 & 0 &0&1&fracendright) begin r_1-r_3\r_2+r_3\phantom\phantomendrightarrow\ rightarrowleft(begin 1 & k &0 &0&frac\ 0 & 1 &0 &0&frac\ 0 & 0 &1&0&frac\ 0 & 0 &0&1&fracendright) begin r_1-kcdot\phantom\phantom\phantomendrightarrow left(begin 1 & 0 &0 &0&frac\ 0 & 1 &0 &0&frac\ 0 & 0 &1&0&frac\ 0 & 0 &0&1&fracendright) $$

Из последней матрицы имеем: $x_1=x_2=x_3=x_4=frac$.

• При $k=-3$ система несовместна.
• При $k=1$ система является неопределённой. Общее решение системы: $left<begin& x_1=-x_2-x_3-x_4+1;\&x_2in,;x_3in,;x_4in. endright.$
• При $kneq$ и $kneq$ система является определённой. Решение системы: $x_1=x_2=x_3=x_4=frac$.

Видео:При каких λ однородная система уравнений имеет ненулевое решение?Скачать

Задача с параметром ЕГЭ 17

Практика (40)

при каких значениях параметра а уравнение х+sqrt(4а-х^2)=sqrt(2ax+4a) имеет единственный корень

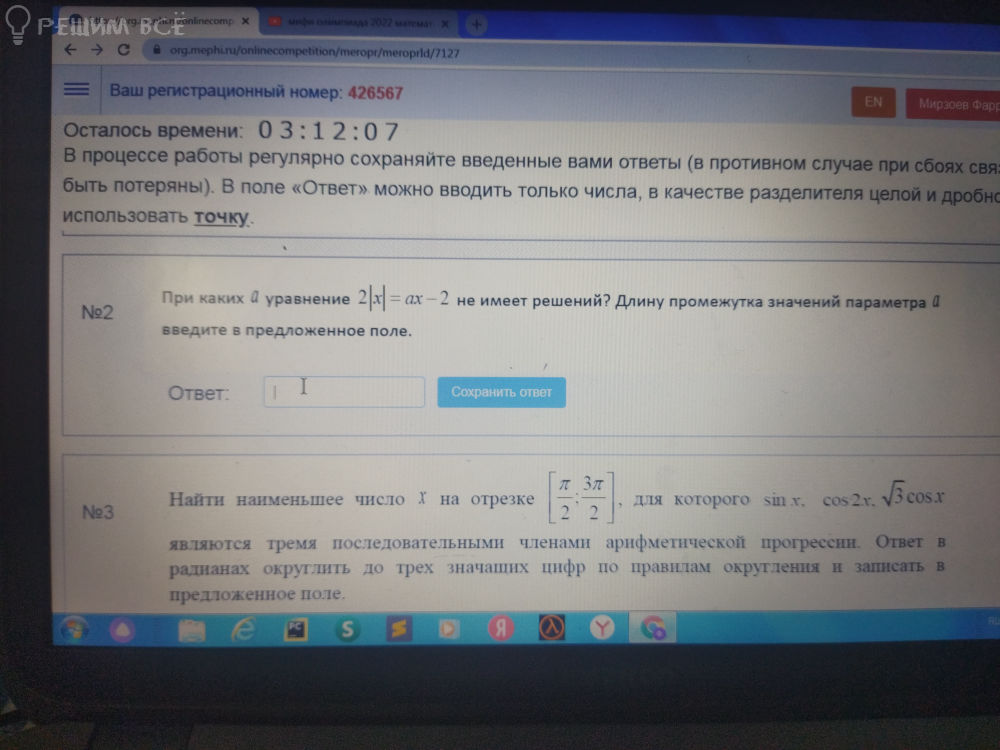
при каких a уравнение 2|x| =ax-2 не имеет решений ?

При каком значении параметра решением неравенства ax2 + (2a –1)x + a – 2 ≤ 0 является вся числовая прямая? Укажите его наибольшее значение.

При каком значении параметра уравнение a2x + 4ax – 6a = 12 – 4x имеет бесконечно много корней?

При каких значениях параметра а неравенство 4^x + (а — 1) * 2^x + 2а — 5 >0 выполнено при всех значениях х?

Найти все значения параметра а, при которых уравнение 3*4^x-2 + 27= а + а*4^x-2 имеет хотя бы одно решение.

При каких значениях параметра а уравнение имеет только одно решение?

11(5). Найдите все значения параметра а ‚ при каждом из которых система уравнений (ay+ax—1)(y+x—a)=0, |о]=а имеет ровно четыре решения.

Найдите все а, при которых системаимеет единственное решение: <х1+ Зах + За? + За +3

Найдите все значения а, при каждом из которых система уравнений x(x^2+y^2-y-2)=|x|(y-2),y=x+a имеет ровно три различных решения.

Найти все значения параметра a, при каждом из которых система уравнений имеет ровно два различных решения

x^2-8a+a^2-6x/x^2+a-8=0 Найти все a, при которых. уравнение имеет ровна 2 решение

При каких значениях параметра а множеством неровности sqrt (1- (x + 2a) ^ 2)> = (4/3)x является промежуток длиной 9/5

(9x^2-36x+36)(a-4)/(2^x-a)≥0
Решите неравенство в зависимости от значений параметра.

Параметр.
1)Решите первое неравенство этой системы
2) Определите множество решений второго неравенства системы в зависимости от значений а
3)Определите все решения системы в зависимости от значений а.

Помогите пожалуйста!! при каком наименьшем [red]a[/red] уравнение имеет хотя бы один корень?

При каких значениях параметра a система
2^(lny)=4^(|x|)
log_(2)(x^(4)y^(2)+2a^(2))=log_(2)(1-ax^(2)y^(2))+1
имеет единственное решение?

(x-2)(x-4)-5(x-2)√((x-4)/(x-2)) =(a-2)(a+3) Найти значения параметра а,при которых равенство имеет только [b]один корень[/b]

sin3x+6cos2x-12sinx=p
При каких значениях параметра р уравнение имеет решение?

Найдите сумму всех значений а при каждом из которых уравнение имеет ровнотодин корень

Найдите все целочисленные значения параметра а, при каждом из которых система
1. sqrt((x-1)^2 + (y-a)^2) + sqrt((x-5)^2 + (y-a)^2) = 4
2. x^2 — |a+1|x — 2a^2 = 3
имеет единственное решение

Найдите все значения а, при каждом из которых уравнение a^2 + 13|x| + 5 sqrt(4x^2+9)= 3a + 3|4x-3a| имеет хотя бы один корень

Найдите все значения а, при каждом из которых уравнение 64x^6 — (3x+a)^3 + 4x^2 — 3x = a имеет более одного корня

Найти все значения параметра а, при каждом из которых уравнение
sin(x+4a) + sin ((x^2 — 6x — 7a)/2) = 4x -x^2 — a
не имеет действительных решений

💥 Видео

СИСТЕМА УРАВНЕНИЙ С ПАРАМЕТРОМ егэ по математике 11 классСкачать

№18. Система уравнений с параметром (профильный ЕГЭ)Скачать

Параметры с нуля до уровня ЕГЭ. Линейные уравнения. Математик МГУСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Найдите все значения а, при каждом из которых система уравнений имеет ровно четыре различных решенияСкачать

Найдите все значения параметра а, при которых система имеет единственное решениеСкачать