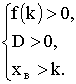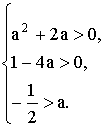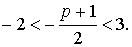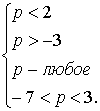При каких значениях параметра а произведение корней уравнения x2 a 1 х а2 3а

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

При каких значениях параметра а произведение корней уравнения x2 a 1 х а2 3а

Вопрос по алгебре:

При каких значениях параметра а произведение корней уравнения x^2+(a+1)x+a²-3a=0 равно 4?
ПОМОГИТЕ ПОЖАЛУЙСТА.
Решите с подробным объяснением

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

-1 не удовлетворяет первому неравенству, поэтому ответ 4

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Задачи с параметрами, сводящиеся к исследованию расположения корней квадратного уравнения

Разделы: Математика

1. Постановка цели урока:

Рассмотрим, как при решении задач с параметрами используются свойства квадратной функции. Задачи разнообразные по форме и содержанию, но объединены обшей идеей — в основе их решения лежат свойства функции: у=ах 2 +bх+с

Дискриминант, старший коэффициент а и х_о=(-b/2а) абсцисса вершины параболы конструируют основу, на которой строится теория решения задач, связанных с квадратичной функцией.

1. При каких значениях параметра а корни уравнения ах 2 -(2а+1)х+За-1=0 больше 1?

Очевидно, что задача равносильна следующей: “при каких значениях параметра, а корни квадратного трехчлена f(х)=ах -(2а+1)х+За-1 больше 1?

Переход от одной формулировки задач к другой дает возможность использовать основную идею решения, которая связана с описанием свойств квадратного трехчлена и с их геометрической интерпретацией.

В частности, чтобы корни квадратного трехчлена f(х)=ах +bх+с (а≠0) были больше числа d (х₁; х₂ > d) необходимо и достаточно выполнение условий:

Скажите, а как можно от совокупности двух систем перейти к одной системе

Мы получим условие того, что корни квадратного трехчлена больше данного числа d. Неплохо бы помнить данное утверждение, однако заучивать его не надо, гораздо важнее понять механизм возникновения необходимости неравенств и научиться его применить при решении конкретных неравенств и научиться его применить при решении конкретных задач. Вернемся к нашей задаче:

1. 
2. а=0

=> х=-1 не удовлетворяет условию задачи

Остается только решить эту систему неравенств (1) при а (1; )

Скажите, а есть ли другой способ задач? (Этот же результат мы получим, решая неравенство x₁>1, где x₁ — меньший корень уравнения.)

• При каких значениях а корни уравнения х 2 -2(а-1)х+2а+1=0 имеют разные знаки и оба по абсолютной величине меньше 4?
• Как можно перефразировать данное задание? (Например, корни квадратичного трехчлена принадлежат промежутку (-4;4)

• Как можно заменить два последних неравенства в данной конкретной задаче, учитывая, что ветви параболы направлены вверх?

Развиваем I — ключевую задачу:

При каких значениях параметра а оба корня уравнения х 2 -ах+2=0 удовлетворяет условию 1 -2 очень сложно.

1. Найти а, при которых число -1 лежит между корнями уравнения х 2 +2ах+4а 2 -а-2=0 Мы варьируем условие! Во второй задаче корень лежит между числами, а в третьей число лежит между корнями.

Вернемся ко второй задаче: обязательно ли условие D≥0?

Развиваем III ключевую задачу:

3sinх+(4-2а)sinх+1 -а =0 имеем корни разного знака? Sinх=1; |t| ≤ 1

3t 2 — (4 — 2а)t +1 — а 2 = 0

f(-1)>0 f(1)>0 (0)>0

a 2 +2a-8 2 -2a 2 -1>0

(a+4)(a-2) 0

Ответ: а (1,2)

При каких а, уравнение соs 2 х-(а-2)соsх+4а+1=0 не имеет корней? cosх=t |t| 2 -4(4a+1) 2 -12a 0
f(-1) б х+cos б х+a*sinхсоsх≥0
sin 4 х-sin 2 хсоs 2 х+соs 4 х+аsinхсоsх≥0
1-3sin 2 хсоs 2 х+аsinхсоsх≥0

Ответ:

7. При каких а корни уравнения х 2 -2х-а +1=0 лежат между корнями уравнения

Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

При каких значениях параметра а произведение корней уравнения x2 a 1 х а2 3а

В.П.Василенков, Р.С. Златин, А.В. Дюндин

Раздел 1 . Уравнения

� 1.4. Уравнения с параметрами .

6. Квадратный трехчлен и параметры

Квадратный трехчлен в школе можно назвать главной функцией всей математики 8-9 классов, а также всей школьной математики.

Особую роль среди уравнений с параметрами играют задачи, связанные с расположением корней квадратного трехчлена. Для решения таких задач можно сформулировать теоремы, но, однако, количество таких теорем будет практически необозримо. И остается только одно- научиться придумывать теорему каждый раз, в каждой конкретной задаче. Для придумывания таких теорем нужно не только знание свойств квадратного трехчлена, но и умение мыслить одновременно на двух языках — алгебраическом и геометрическом.

Это значит, что для любого свойства, сформулированного на алгебраическом языке, нужно уметь дать геометрическую интерпретацию на графике, и наоборот. Например:

� старший коэффициент меньше нуля — значит ветви параболы направлены вниз;

� график функции у = ах 2 + bх + с находится выше оси абсцисс- значит а>0, b 2 — 4ac

Рассмотрим ряд примеров.

Пример 1. При каких значениях параметра а корни квадратного уравнения х 2 + (а + 1)х + 3 = 0 лежат по разные стороны от числа 2?

Построим график квадратного трехчлена, удовлетворяющий данному условию. Если потребовать, чтобы f(2) 2 + (a + 1)x + 3, то отсюда будет следовать, что корни уравнения существуют и лежат по разные стороны от числа 2. Верно и обратное, то есть справедлива следующая теорема.

Теорема. Для того, чтобы корни квадратного уравнения х 2 + рх + q = 0 лежали по разные стороны от числа к необходимо и достаточно, чтобы f(k)

В нашем случае f(2) = 4 + 2(а + 1) + 3 = 2а + 9, 2а + 9 Ответ: а

Пример 2. Найти все а, при которых корни уравнения х 2 + х + а = 0 различные и оба больше а.

Дадим геометрическую интерпретацию поставленной задачи (рис.9). Очевидно, что если f(a) > 0, х_в > a и D > 0, то оба корня действительно различны и оба больше а. Ни одно из условий не является лишним.

Например, если отбросить условие D > 0, то возможна ситуация (см. рис. 10) и корней вообще нет, хотя f(a) > 0, x_в > а.

Если отбросить условие f(a) > 0, то возможна ситуация (см. рис.11) и один корень меньше а, другой больше a , хотя D > 0 и х_в > а.

Если отбросить условие х_в > а, то возможна ситуация (см. рис. 12) и корни уравнения меньше а, хотя D > 0 и f(a) > 0.

Теорема. Для того, чтобы корни уравнения х 2 + рх + q = 0 были различны и оба больше к необходимо и достаточно, чтобы выполнялись условия:

В нашем примере f(a) = а 2 + а + а = а 2 + 2а, D = 1 — 4а, х_в = — .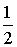

Получаем систему неравенств.

Систему решаем методом интервалов (рис. 13).

Ответ: а .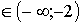

Пример 3. Найти все значения параметра р, при которых корни уравнения х 2 + (р + 1)х + р = 0 принадлежат промежутку (-2;3).

Дадим геометрическую интерпретацию этой задачи (см. рис.14).Очевидно, что если f(-2) > 0, f(3) > 0, D 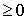, -2

Итак, в нашем случае f(-2) = 4 — 2(p + 1) + p = 2 — p,

f(3) = 9 + 3(p + 1) + p = 12 + 4p,

D = (p + 1) 2 — 4p = (p — 1) 2 ,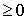

Итак, имеем систему неравенств:

или

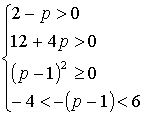
Пример 4. При каких а уравнение (1 + 2а)х 4 — 2ах 2 + (1 + а) = 0:

1) не имеет действительных корней;

2) имеет один корень;

3) имеет два корня;

4) имеет три корня;

5) имеет четыре корня.

Введем новую переменную у = х 2 . Тогда заданное уравнение равносильно уравнению (1 + 2а)у 2 — 2ау + (1 + а) = 0, где у = х 2 .

Изложим схему исследования.

1. Уравнение (1 + 2а)у 2 — 2ау + (1 + а) = 0 , где у = х 2 не имеет решений в трех случаях:

1) D = (2а) 2 — 4(1 + а)(1 + 2а)

2) D 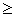0 и у₁

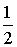
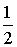
3) а = — (тогда у = — ).

2. Система имеет один корень:

3. Система имеет два корня в случаях:

2)D > 0, у₁ 0 (корни находятся по разные стороны от нуля.)

4. Система имеет три корня, если D > 0, у₁ > 0, у₂ = 0.

5. Система имеет четыре корня, если D > 0, у₁ > 0, у₂ > 0 (оба корня правее нуля.)

Дальнейшее исследование проводится аналогично предыдущим случаям. Получите решение самостоятельно!

7. Теорема Виета и параметры.

Многие уравнения с параметрами связаны с использованием теоремы Виета. При этом важно понимать, что теорема Виета в школьном курсе формулируется только для случая, когда существуют действительные корни уравнения, в противном случае можем получить ошибочный ответ (см. пункт 4 примеров 1 и 2).

Приведем некоторые примеры, в которых используется теорема Виета.

Пример 1. При каких а разность корней уравнения 2х 2 — (а + 1)х + (а — 1) =0 равна их произведению?

Прежде всего заметим, что теорема Виета применима при любом а, так как

D = (а + 1) 2 — 8(а — 1) = а 2 — 6а + 9 = (а — 3) 2 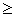0.

По теореме Виета 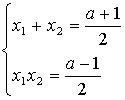и кроме того х₁-х₂ = х₁х₂,

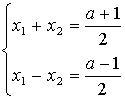
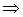
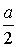
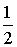
тогда х₁= , х₂= .

Тогда 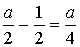, а = 2.

Пример 2. Найти наименьшее значение выражения х₁ 2 + х₂ 2 , если х₁ и х₂ � корни уравнения х 2 — 2ах + а + 6 = 0.

По теореме Виета х₁+ х₂ = 2а,

Казалось бы, мы должны найти наименьшее значение выражения 4а 2 — 2а — 12, а оно достигается в вершине параболы у = 4а 2 — 2а — 12,

, и а = .

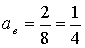
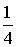
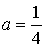
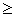
На самом деле мы опять допускаем ту же ошибку, т. е. если подставить в уравнение, то оно не имеет решений. Поэтому мы должны найти, при каких а теорема Виета применима, то есть D = 4а 2 — 4а — 24 0.

Решая неравенство, получим 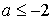или .

Из графика функции у = 4а 2 — 2а — 12 (см. рис. 16) видно, что наименьшее значение будет среди двух чисел f (-2) и f (3):

Итак, наименьшее значение выражения х₁ + х₂ равно 8 при а = -2.

Упражнения

4.1. .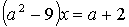

4.2. .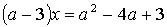

4.3. .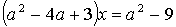

4.4. .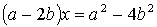

4.5. .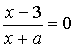

4.6. .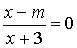

4.7. 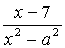=0.

4.8. .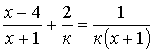

4.9. .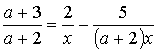

4.10. .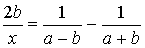

4.11. .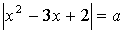

4.12. .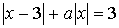

4.13. .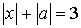

4.14. Найти все значения параметра а, для которых квадратное уравнение :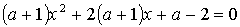

а) имеет два корня;

б) имеет один корень;

в) не имеет корней.

4.15. .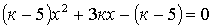

4.16. .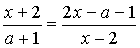

4.17. .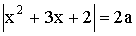

4.18. .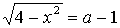

4.19. .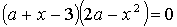

4.20. При каких а уравнение 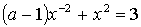имеет единственное решение?

4.21. При каких а интервал (2;3) находится между корней уравнения ?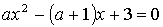

Указание. Рассмотреть два случая: 1) a >0; 2) a

4.22. При каких m уравнение 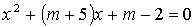имеет один корень больше 2, другой меньше 2?

4.23. При каких к корни уравнения 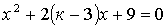принадлежат интервалу (-6;1)?

4.24. Найти все р, при которых один корень уравнения 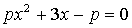больше 3, другой � меньше 2.

4.25. Вычислить сумму корней уравнения 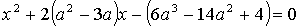и найти значение а, при котором соответствующая эта сумма принимает наибольшее значение.

Указание : х₁ + х₂ = 6а — 2а 2 . Требуется найти наибольшее значение 6а — 2а 2 при условии, что D 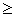0.

4.26. Решить уравнение .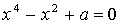

4.27. При каких а уравнение :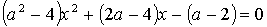

1) имеет не более одного решения;

2) не менее одного решения.

Обязательно самостоятельно выполните

1.1(а,в); 1.2(а); 1.3(а); 2.4; 2.13; 3.1; 3.5; 4.2; 4.6; 4.9.

1.2(б); 1.4; 2.12; 2.15; 3.10; 4.14; 4.16; 4.21; 4.23; 4.25.

📽️ Видео

При каких значениях параметра уравнение имеет единственный кореньСкачать

При каких значениях а сумма квадратов корней уравнения x² + ax + a - 2 = 0 минимальна?Скачать

Уравнения с параметром. Алгебра, 8 классСкачать

#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Найти значение суммы и произведения корней квадратного уравненияСкачать

Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать

Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Параметры с нуля. Урок 6. Квадратные уравнения с параметром. 17 задание ЕГЭ профильная математикаСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Профильный ЕГЭ 2023. Задача 17. Параметры. Методы решенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать